Теоретические основы решения уравнений
Наиболее важные приемы преобразования уравнений
Методы решения иррациональных уравнений
Метод сведения к эквивалентной системе уравнений и неравенств
Метод введения новой переменной
Метод сведения к эквивалентным системам рациональных уравнений
Умножение обеих частей уравнения на функцию
Использование ОДЗ
Тождественные преобразования при решении иррациональных уравнений
Теоретические основы решения иррациональных неравенств
Умножение обеих частей неравенства на функцию
Решение иррациональных неравенств с использованием свойств входящих в них функций
Использование графиков функций
Рациональность дробно-линейных иррациональностей
Рационализация квадратичных иррациональностей посредством подстановок Эйлера
Рационализация с помощью тригонометрических подстановок
Навигация
Метод сведения к эквивалентным системам рациональных уравнений
Методика решения иррациональных уравнений и неравенств в школьном курсе математики
98604
знака
5
таблиц
19
изображений
2.2.4. Метод сведения к эквивалентным системам рациональных уравнений
Уравнения вида 
(здесь a, b, c, d – некоторые числа, m, n – натуральные числа) и ряд других уравнений часто удается решить при помощи введения двух вспомогательных неизвестных: 
и 
, где 
и последующего перехода к эквивалентной системе рациональных уравнений. [17]
Пример 16. Решить уравнение 
.
Решение. Введем новые переменные
и 
, где .
Тогда исходное уравнение принимает вид: 
. Полученное уравнение обладает одним существенным недостатком: в нем две неизвестных. Но заметим, что величины y и z не являются независимыми переменными – они зависят одна от другой посредством старой переменной x. Выразим x через y и z: 
и 
. Теперь, можно заметить, что если первое уравнение умножить на два и затем вычесть из него второе, то переменная x исключается, и остается связь только между y и z
.
В результате получаем систему двух уравнений относительно двух неизвестных y и z
Решая эту систему методом подстановки, приходим к уравнению 
, корнями которого являются числа 
и 
. Корень 
посторонний, поскольку 
. Осталось решить уравнение 
, откуда находим 
.
Ответ. .
Пример 17. Решить уравнение 
. [6]
Решение. Возведение обеих частей этого уравнения в четвертую степень не обещает ничего хорошего. Если же положить 
, 
, то исходное уравнение переписывается так: . Поскольку мы ввели две новые неизвестные, надо найти еще одно уравнение, связывающее y и z. Для этого возведем равенства , в четвертую степень и заметим, что 
.
Итак, надо решить систему уравнений
она имеет два (действительных) решения: 
, 
; 
, 
.
Остается решить систему двух уравнений с одним неизвестным
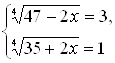
и систему
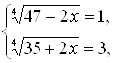
первая из них дает 
, вторая дает 
.
Ответ: , .
Не всегда после введения новых переменных удается исключить неизвестную x, как это было в рассмотренных Примерах 15, 16. Однако, как можно убедиться из следующего примера, переход от уравнения к системе может помочь и в таком случае. [17]
Пример 18. Решить уравнение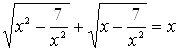 
.
Решение. Введем новые переменные
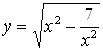и 
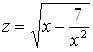, где .
По стандартной схеме получим следующую систему уравнений:
откуда следует, что
.
Так как 
, то y и z должны удовлетворять системе
Возведем оба уравнения этой системы в квадрат, после чего, сложив их, получаем уравнение 
.
Также возведем равенства 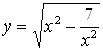, 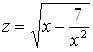в квадрат и заметим, что 
.
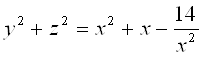Получаем следующую систему уравнений:
из которой получаем уравнение 
.
Заметим, что это уравнение имеет корень . Тогда, разделив многочлен на 
, получаем разложение левой части уравнения на множители
.
Отсюда следует, что – единственное решение этого уравнения. После проверки записываем это решение в ответ.
Ответ: .
Похожие работы
... на основе знания связи между результатом и компонентами арифметических действий (т.е. знания способов нахождения неизвестных компонентов). Эти требования программы определяют методику работы над уравнениями. 2. Методика изучения неравенств в старших классах 2.1 Содержание и роль линии уравнений и неравенств в современном школьном курсе математики Ввиду важности и обширности материала, ...
... на качественно новую ступень овладения содержанием школьной математики. Глава II. Методико - педагогические основы использования самостоятельной работы, как средство обучения решению уравнений в 5 - 9 классах. § 1. Организация самостоятельной работы при обучения решению уравнений в 5 - 9 классах. При традиционном способе преподавания учитель часто ставит ученика в положение объекта ...
... , можно сделать вывод о недостаточном освещении изучаемого вопроса в современной методической литературе. Объект исследования работы: процесс обучения математике. Предмет: формирование умения решения квадратных уравнений у учащихся 8-го класса. Контингент: учащиеся 8-го класса. Глава 1. Теоретические аспекты обучению решения уравнений в 8 классе 1.1. Из истории возникновения квадратных ...
... числового аргумента, поэтому при таком подходе наблюдается определённая избыточность в формировании функции как обобщённого понятия. 2. Основные направления введения понятия функции в школьном курсе математики В современном школьном курсе математики ведущим подходом считается генетический с добавлением элементов логического. Формирование понятий и представлений, методов и приёмов в составе ...
0 комментариев