Теоретические основы решения уравнений
Наиболее важные приемы преобразования уравнений
Методы решения иррациональных уравнений
Метод сведения к эквивалентной системе уравнений и неравенств
Метод введения новой переменной
Метод сведения к эквивалентным системам рациональных уравнений
Умножение обеих частей уравнения на функцию
Использование ОДЗ
Тождественные преобразования при решении иррациональных уравнений
Теоретические основы решения иррациональных неравенств
Умножение обеих частей неравенства на функцию
Решение иррациональных неравенств с использованием свойств входящих в них функций
Использование графиков функций
Рациональность дробно-линейных иррациональностей
Рационализация квадратичных иррациональностей посредством подстановок Эйлера
Рационализация с помощью тригонометрических подстановок
Навигация
Методы решения иррациональных уравнений
Методика решения иррациональных уравнений и неравенств в школьном курсе математики
98604
знака
5
таблиц
19
изображений
2.2. Методы решения иррациональных уравнений
В работе будем придерживаться следующего определения иррационального уравнения:
Иррациональным уравнением называется уравнение, содержащее неизвестное под знаком корня.
Прежде чем приступить к решению сложных уравнений учащиеся должны научиться решать простейшие иррациональные уравнения. К простейшим иррациональным уравнениям относятся уравнения вида: 
.
Основная идея решения иррационального уравнения состоит в сведении его к рациональному алгебраическому уравнению, которое либо равносильно исходному иррациональному уравнению, либо является его следствием.
Главный способ избавиться от корня и получить рациональное уравнение – возведение обеих частей уравнения в одну и ту же степень, которую имеет корень, содержащий неизвестное, и последующее «освобождение» от радикалов по формуле 
. [6]
Если обе части иррационального уравнения возвести в одну и ту же нечетную степень и освободиться от радикалов, то получится уравнение, равносильное исходному. [6]
При возведении уравнения в четную степень получается уравнение, являющееся следствием исходного. Поэтому возможно появление посторонних решений уравнения, но не возможна потеря корней. Причина приобретения корней состоит в том, что при возведении в четную степень чисел, равных по абсолютной величине, но разных по знаку, получается один и тот же результат.
Так как могут появиться посторонние корни, то необходимо делать проверку, подставляя найденные значения неизвестной только в первоначальное уравнение, а не в какие-то промежуточные.
Рассмотрим применение данного метода для решения иррациональных уравнений вида 
. [7]
Пример 1. Решить уравнение 
.
Решение. Возведем обе части этого уравнения в квадрат 
и получим 
, откуда следует, что 
или 
.
Проверка. : 
. Это неверное числовое равенство, значит, число 
не является корнем данного уравнения.
: 
. Это верное числовое равенство, значит, число 
является корнем данного уравнения.
Ответ. .
Пример 2. Решить уравнение 
.
Решение. После возведения в квадрат получаем уравнение 
, откуда следует что 
или 
.
Проверка. : 
. Это верное числовое равенство, значит, число 
является корнем данного уравнения.
: 
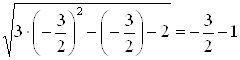
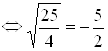. Это неверное числовое равенство, значит, число 
не является корнем данного уравнения.
Ответ. .
Похожие работы
... на основе знания связи между результатом и компонентами арифметических действий (т.е. знания способов нахождения неизвестных компонентов). Эти требования программы определяют методику работы над уравнениями. 2. Методика изучения неравенств в старших классах 2.1 Содержание и роль линии уравнений и неравенств в современном школьном курсе математики Ввиду важности и обширности материала, ...
... на качественно новую ступень овладения содержанием школьной математики. Глава II. Методико - педагогические основы использования самостоятельной работы, как средство обучения решению уравнений в 5 - 9 классах. § 1. Организация самостоятельной работы при обучения решению уравнений в 5 - 9 классах. При традиционном способе преподавания учитель часто ставит ученика в положение объекта ...
... , можно сделать вывод о недостаточном освещении изучаемого вопроса в современной методической литературе. Объект исследования работы: процесс обучения математике. Предмет: формирование умения решения квадратных уравнений у учащихся 8-го класса. Контингент: учащиеся 8-го класса. Глава 1. Теоретические аспекты обучению решения уравнений в 8 классе 1.1. Из истории возникновения квадратных ...
... числового аргумента, поэтому при таком подходе наблюдается определённая избыточность в формировании функции как обобщённого понятия. 2. Основные направления введения понятия функции в школьном курсе математики В современном школьном курсе математики ведущим подходом считается генетический с добавлением элементов логического. Формирование понятий и представлений, методов и приёмов в составе ...
0 комментариев