Теоретические основы решения уравнений
Наиболее важные приемы преобразования уравнений
Методы решения иррациональных уравнений
Метод сведения к эквивалентной системе уравнений и неравенств
Метод введения новой переменной
Метод сведения к эквивалентным системам рациональных уравнений
Умножение обеих частей уравнения на функцию
Использование ОДЗ
Тождественные преобразования при решении иррациональных уравнений
Теоретические основы решения иррациональных неравенств
Умножение обеих частей неравенства на функцию
Решение иррациональных неравенств с использованием свойств входящих в них функций
Использование графиков функций
Рациональность дробно-линейных иррациональностей
Рационализация квадратичных иррациональностей посредством подстановок Эйлера
Рационализация с помощью тригонометрических подстановок
Навигация
Использование ОДЗ
Методика решения иррациональных уравнений и неравенств в школьном курсе математики
98604
знака
5
таблиц
19
изображений
2. Использование ОДЗ
Иногда знание ОДЗ позволяет доказать, что уравнение не имеет решений, а иногда позволяет найти решения уравнения непосредственной подстановкой чисел из ОДЗ.
Пример 26. Решить уравнение 
.
Решение. ОДЗ этого уравнения состоит из всех 
, одновременно удовлетворяющих условиям 
и 
, то есть ОДЗ есть пустое множество. Этим решение уравнения завершается, так как установлено, что ни одно число не может являться решением, то есть уравнение не имеет корней.
Ответ: Корней нет.
Пример 27. Решить уравнение 
.
Решение. Конечно, это иррациональное уравнение можно решить путем традиционного возведения обеих частей в квадрат. Однако, найдя ОДЗ этого уравнения, приходим к выводу, что ОДЗ исходного уравнения – одноэлементное множество {2}. Подставив 
в данное уравнение, приходим к выводу, что – корень исходного уравнения.
Ответ: .
3. Использование графиков функций
При решении уравнений или неравенств иногда полезно рассмотреть эскиз графиков их правой и левой частей в одной и той же системе координат. Тогда этот эскиз графиков поможет выяснить, на какие множества надо разбить числовую ось, чтобы на каждом из них решение уравнения (или неравенства) было очевидно.
Обратим внимание, что эскиз графика лишь помогает найти решение, но писать, что из графика следует ответ, нельзя, ответ еще надо обосновать.
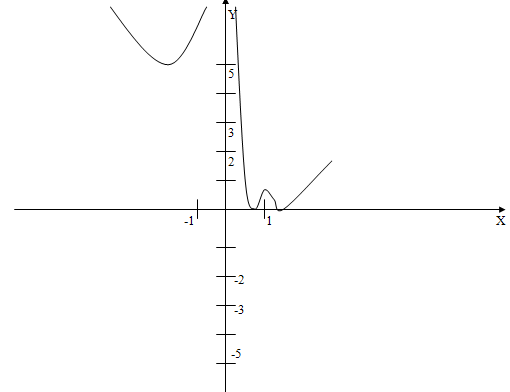
Пример 28. Решить уравнение 
.
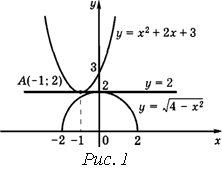
Решение. ОДЗ данного уравнения есть все из промежутка 
. Эскизы графиков функций 
и 
представлены на рисунке 1.
Проведем прямую 
. Из рисунка следует, что график функции 
лежит не ниже этой прямой, а график функции 
не выше. При этом эти графики касаются прямой в разных точках. Следовательно, уравнение не имеет решений. Докажем это. Для каждого 
имеем 
, а 
. При этом 
только для 
, а 
только для 
. Это означает, что исходное уравнение не имеет корней.
Ответ: Корней нет.
Пример 29. Решить уравнение 
.
Решение. Эскизы графиков функций 
и 
представлены на рисунке 2.
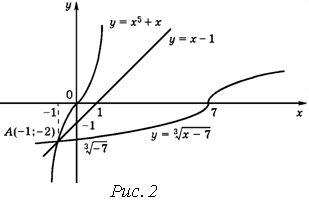
Легко проверяется, что точка 
является точкой пересечения графиков функций и , то есть – решение уравнения. Проведем прямую 
. Из рисунка следует, что она расположена между графиками функций 
и 
. Это наблюдение и помогает доказать, что других решений данное уравнение не имеет.
Для этого докажем, что для из промежутка 
справедливы неравенства 
и 
, а для промежутка 
справедливы неравенства 
и 
. Очевидно, что неравенство справедливо для 
, а неравенство для 
. Решим неравенство . Это неравенство равносильно неравенству 
, которое можно переписать в виде 
. Решениями этого неравенства являются все . Точно также показывается, что решениями неравенства 
являются все .
Следовательно, требуемое утверждение доказано, и исходное уравнение имеет единственный корень .
Ответ: .
Кроме рассмотренных типов иррациональных уравнений существуют еще и уравнения смешанного типа. К этой группе относятся иррациональные уравнения, содержащие кроме знака радикала и другие выражения (логарифмическое, показательное, тригонометрическое), а также знак модуля и параметр. Уравнения данного типа также чаще всего включаются в задания ЕГЭ и программу вступительных экзаменов в ВУЗы.
Со всеми учащимися на уроке такие уравнения разбирать не нужно, но они могут быть рассмотрены в рамках факультативных или кружковых занятий по математике с учащимися, повышенный интерес к математике. Примеры решения уравнений смешанного типа помещены в приложении А.
Похожие работы
... на основе знания связи между результатом и компонентами арифметических действий (т.е. знания способов нахождения неизвестных компонентов). Эти требования программы определяют методику работы над уравнениями. 2. Методика изучения неравенств в старших классах 2.1 Содержание и роль линии уравнений и неравенств в современном школьном курсе математики Ввиду важности и обширности материала, ...
... на качественно новую ступень овладения содержанием школьной математики. Глава II. Методико - педагогические основы использования самостоятельной работы, как средство обучения решению уравнений в 5 - 9 классах. § 1. Организация самостоятельной работы при обучения решению уравнений в 5 - 9 классах. При традиционном способе преподавания учитель часто ставит ученика в положение объекта ...
... , можно сделать вывод о недостаточном освещении изучаемого вопроса в современной методической литературе. Объект исследования работы: процесс обучения математике. Предмет: формирование умения решения квадратных уравнений у учащихся 8-го класса. Контингент: учащиеся 8-го класса. Глава 1. Теоретические аспекты обучению решения уравнений в 8 классе 1.1. Из истории возникновения квадратных ...
... числового аргумента, поэтому при таком подходе наблюдается определённая избыточность в формировании функции как обобщённого понятия. 2. Основные направления введения понятия функции в школьном курсе математики В современном школьном курсе математики ведущим подходом считается генетический с добавлением элементов логического. Формирование понятий и представлений, методов и приёмов в составе ...
0 комментариев