Теоретические основы решения уравнений
Наиболее важные приемы преобразования уравнений
Методы решения иррациональных уравнений
Метод сведения к эквивалентной системе уравнений и неравенств
Метод введения новой переменной
Метод сведения к эквивалентным системам рациональных уравнений
Умножение обеих частей уравнения на функцию
Использование ОДЗ
Тождественные преобразования при решении иррациональных уравнений
Теоретические основы решения иррациональных неравенств
Умножение обеих частей неравенства на функцию
Решение иррациональных неравенств с использованием свойств входящих в них функций
Использование графиков функций
Рациональность дробно-линейных иррациональностей
Рационализация квадратичных иррациональностей посредством подстановок Эйлера
Рационализация с помощью тригонометрических подстановок
Навигация
Метод введения новой переменной
Методика решения иррациональных уравнений и неравенств в школьном курсе математики
98604
знака
5
таблиц
19
изображений
2.2.3. Метод введения новой переменной.
Мощным средством решения иррациональных уравнений является метод введения новой переменной, или «метод замены». Метод обычно применяется в случае, если в уравнении неоднократно встречается некоторое выражение, зависящее от неизвестной величины. Тогда имеет смысл обозначить это выражение какой-нибудь новой буквой и попытаться решить уравнение сначала относительно введенной неизвестной, а потом уже найти исходную неизвестную. В ряде случаев удачно введенные новые неизвестные иногда позволяют получить решение быстрее и проще; иногда же без замены решить задачу вообще невозможно. [6], [17]
Пример 7. Решить уравнение 
.
Решение. Положив 
, получим существенно более простое иррациональное уравнение 
. Возведем обе части уравнения в квадрат: 
.
Далее последовательно получаем:
;
;
;
;
, 
.
Проверка найденных значений их подстановкой в уравнение показывает, что – корень уравнения, а – посторонний корень.
Возвращаясь к исходной переменной x, получаем уравнение 
, то есть квадратное уравнение 
, решив которое находим два корня: 
,
. Оба корня, как показывает проверка, удовлетворяют исходному уравнению.
Ответ: , .
Замена особенно полезна, если в результате достигается новое качество, например, иррациональное уравнение превращается в квадратное.
Пример 8. Решить уравнение 
.
Решение. Перепишем уравнение так: 
.
Видно, что если ввести новую переменную 
, то уравнение примет вид 
, откуда 
, 
.
Теперь задача сводится к решению уравнения 
и уравнения 
. Первое из этих решений не имеет, а из второго получаем 
, 
. Оба корня, как показывает проверка, удовлетворяют исходному уравнению.
Ответ. , .
Отметим, что «бездумное» применение в Примере 8 метода «уединения радикала» и возведение в квадрат привело бы к уравнению четвертой степени, решение которого представляет собой в общем случае чрезвычайно сложную задачу.
Пример 9. Решить уравнение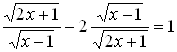 
.
Введем новую переменную
, 
.
В результате исходное иррациональное уравнение принимает вид квадратного
,
откуда учитывая ограничение , получаем 
. Решая уравнение 
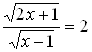, получаем корень 
. Как показывает проверка, удовлетворяет исходному уравнению.
Ответ. .
Иногда посредством некоторой подстановки удается привести иррациональное уравнение к рациональному виду, как рассмотренных Примерах 8, 9. В таком случае говорят, что эта подстановка рационализирует рассматриваемое иррациональное уравнение, и называют ее рационализирующей., основанный на применении рационализирующих подстановок, называется способом рационализации.
Со всеми учащимися на уроке этот способ решения иррациональных уравнений разбирать не нужно, но он может быть рассмотрен в рамках факультативных или кружковых занятий по математике с учащимися, проявляющих повышенный интерес к математике.
Похожие работы
... на основе знания связи между результатом и компонентами арифметических действий (т.е. знания способов нахождения неизвестных компонентов). Эти требования программы определяют методику работы над уравнениями. 2. Методика изучения неравенств в старших классах 2.1 Содержание и роль линии уравнений и неравенств в современном школьном курсе математики Ввиду важности и обширности материала, ...
... на качественно новую ступень овладения содержанием школьной математики. Глава II. Методико - педагогические основы использования самостоятельной работы, как средство обучения решению уравнений в 5 - 9 классах. § 1. Организация самостоятельной работы при обучения решению уравнений в 5 - 9 классах. При традиционном способе преподавания учитель часто ставит ученика в положение объекта ...
... , можно сделать вывод о недостаточном освещении изучаемого вопроса в современной методической литературе. Объект исследования работы: процесс обучения математике. Предмет: формирование умения решения квадратных уравнений у учащихся 8-го класса. Контингент: учащиеся 8-го класса. Глава 1. Теоретические аспекты обучению решения уравнений в 8 классе 1.1. Из истории возникновения квадратных ...
... числового аргумента, поэтому при таком подходе наблюдается определённая избыточность в формировании функции как обобщённого понятия. 2. Основные направления введения понятия функции в школьном курсе математики В современном школьном курсе математики ведущим подходом считается генетический с добавлением элементов логического. Формирование понятий и представлений, методов и приёмов в составе ...
0 комментариев