Навигация
Использование графиков функций
3. Использование графиков функций
Пример 17. Решить неравенство ![]() .
.
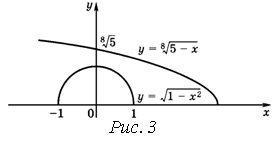 |
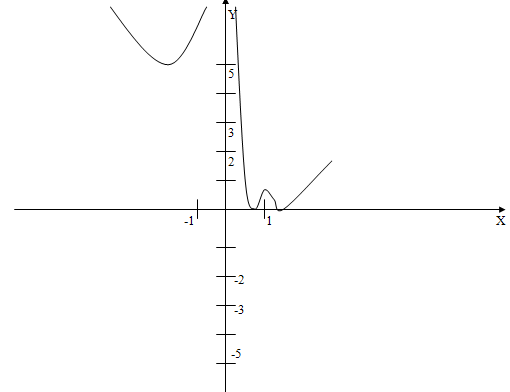
Решение. ОДЗ этого неравенства есть все
Докажем это. Для каждого ![]() из промежутка
из промежутка ![]() имеем
имеем ![]() , а для каждого такого
, а для каждого такого ![]() имеем
имеем ![]() . Значит, для каждого
. Значит, для каждого ![]() имеем
имеем ![]() . Следовательно, решениями исходного неравенства будут все
. Следовательно, решениями исходного неравенства будут все ![]() из промежутка
из промежутка ![]() .
.
Ответ: ![]()
§ 4. Опытное преподавание
Опытное преподавание применяется для объективной и достоверной проверки гипотезы и предполагает одновременное использование целого ряда методов, например, наблюдение, диагностирующие контрольные работы, беседа и другие.
Одной из задач опытного преподавания являлась проверка эффективности разработанного факультативного курса по изучению иррациональных уравнений, как предусмотренных школьной программой, так и не встречающихся в школьном курсе математики. Курс рассчитан на систематизацию методов решения иррациональных уравнений. Необходимо рассмотреть основные виды иррациональных уравнений наиболее часто встречаемых на выпускных и вступительных экзаменах.
Цели факультативных занятий:
1. Познакомить учащихся с некоторыми методами решения иррациональных уравнений.
2. Показать применение различных методов при решении уравнений одного вида.
3. Формировать умение видеть рациональный метод для решения конкретных видов уравнений.
4. Формировать логическое мышление.
5. Формировать настойчивость, целеустремленность, трудолюбие через решение сложных задач.
6. Развивать математическую речь с присущей ей краткостью, точностью и лаконичностью.
7. Подготовить учащихся к поступлению в ВУЗы.
Знания и умения, которыми должны владеть учащиеся перед изучением факультативного курса по теме «Иррациональные уравнения и методы их решения»:
1. Владеть основными понятиями, относящимися к уравнениям и неравенствам: корень уравнения, ОДЗ уравнения, знать, что значит решить уравнение.
2. Владеть определениями понятий арифметического квадратного корня и арифметического корня ![]() -ой степени.
-ой степени.
3. Знать свойства арифметического квадратного корня и свойства арифметического корня ![]() -ой степени.
-ой степени.
4. Уметь решать простейшие иррациональные уравнения.
5. Уметь решать простейшие тригонометрические, показательные и логарифмические уравнения.
6. Уметь решать линейные и квадратные уравнения.
Кроме того, учащиеся должны иметь представление об общих методах решения уравнений: метод замены, метод разложения на множители, функционально-графический метод.
Цель курса: исследование возможности изучения дополнительно к учебному плану некоторых типов иррациональных уравнений, углубления уже имеющихся знаний по решению иррациональных уравнений.
Этапы курса:
1. Разработка программы факультативных занятий «Иррациональные уравнения и методы их решения» для учащихся 11 класса.
2. Проведение диагностирующей контрольной работы №1.
3. Проведение разработанной программы факультативных занятий.
4. Проведение диагностирующей контрольной работы №2.
5. Анализ полученных результатов опытной работы.
Этап №1
Разработка программы факультативных занятий «Иррациональные уравнения и методы их решения» для учащихся 11 класса.
Факультативные занятия были разработаны на основе анализа математической, методической и учебной литературы.
Этап №2
Проведение диагностирующей контрольной работы №1.
Контрольная работа была проведена перед проведением факультативных занятий с учениками 11а класса школы №37 города Кирова. Ее основная задача: определить уровень подготовки, знаний и умений по теме «Иррациональные уравнения».
Учащимся было предложено 8 заданий, которые было необходимо выполнить в течение 1 часа. В классе 25 человек. Содержание диагностирующей контрольной работы №1 представлено в приложении Б.
Задания 1-3 –с выбором ответа, задания 4-7 – с кратким ответом, задание 8 – с развернутым ответом.
Результаты диагностирующей контрольной работы №1 отображены в таблице №1:
| № задания | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| Кол-во человек, решивших задание | 18 | 17 | 18 | 10 | 7 | 6 | 3 | 0 |
| Доля человек, решивших задание в процентах | 72% | 68% | 72% | 40% | 28% | 24% | 12% | 0% |
Этап №3
Проведение разработанной программы факультативных занятий.
Разработанные задания проводились 2 раза в неделю. Всего было проведено 6 занятий по 2 часа.
Основные задачи проведения факультативных занятий:
1) проверить правильность отбора содержания и системы упражнений;
2) выявить тот материал, который вызывает у учащихся наибольшие затруднения;
3) определить эффективность усвоения материала посредством текущей проверки;
4) выявить заинтересованность учащихся в изучении данной темы.
Этап №4
Проведение диагностирующей контрольной работы №2.
Контрольная работа была проведена после проведения факультативных занятий разработанной программы. Задача: выявление знаний и умений решать иррациональные уравнения.
Учащимся было предложено 8 заданий, которые было необходимо выполнить в течении 1 часа. Содержание диагностирующей контрольной работы №1 представлено в приложении Б.
Тематика заданий та же, что и в контрольной работе №1.
Результаты диагностирующей контрольной работы №2 отображены в таблице №2:
| № задания | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| Кол-во человек, решивших задание | 24 | 23 | 24 | 17 | 11 | 10 | 5 | 3 |
| Доля человек, решивших задание в процентах | 96% | 92% | 96% | 68% | 44% | 40% | 20% | 12% |
Этап №5
Анализ полученных результатов опытной работы.
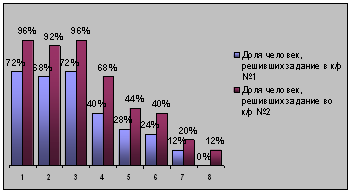 |
На основании таблиц №1 и №2 можно построить диаграмму, отображающую сравнение результатов контрольных работ, проведенных перед посещением учащимися факультативных занятий и после их посещения.
Как видно из диаграммы, перед проведением факультативных занятий уровень знаний учащихся был средним, а после проведения занятий он повысился. Положительная тенденция заметна: учащиеся научились решать простейшие иррациональные уравнения и справились с заданиями 1-3, значительно лучше стало умение решать более сложные уравнения. Так как 8-ое задание относится к высокому уровню сложности, с ним справилось лишь 3 человека. Учащиеся лучше стали владеть методом введения новых переменных при решении иррациональных уравнений. Трудным показался материал, связанный с рационализирующими подстановками при решении иррациональных уравнений.
Программа факультативных занятий на тему «Иррациональные уравнения и методы их решения»
Ниже предлагается программа факультативных занятий на тему «Иррациональные уравнения и методы их решения». Курс лучше изучать в 11 классе, так как уравнения такого вида содержатся в заданиях ЕГЭ и на вступительных экзаменах в ВУЗы. Программа рассчитана на 16 часов. Занятия проводятся по 2 часа.
Занятие №1
Тема: Равносильные и неравносильные преобразования уравнений.
Цели:
1) Познакомить учащихся с понятием равносильных уравнений.
2) Показать, когда одно уравнение является следствием другого.
3) Сформулировать теоремы о равносильности уравнений.
4) Познакомить учащихся с равносильными и неравносильными преобразованиями уравнений.
Краткое содержание: Определение равносильности уравнений, следствия уравнений, понятие постороннего корня уравнения, перечисление и демонстрация на примерах равносильных и неравносильных преобразований уравнений.
Литература для учителя:
Литература для ученика:
Занятие №2, №3
Тема: Решение простейших иррациональных уравнений
Цели:
1) Отработать у учащихся умение решать простейшие иррациональные уравнения вида ![]() ,
, ![]() .
.
2) Закрепить изученный ранее материал.
3) Подготовить учащихся к изучению нового материала.
Краткое содержание: Определение иррационального уравнения, решение простейших иррациональных уравнений вида ![]() ,
, ![]() методом возведения обеих частей уравнения в одну и ту же степень с последующей проверкой полученных корней, а также методом сведения к равносильной системе уравнений и неравенств. Метод уединения радикала.
методом возведения обеих частей уравнения в одну и ту же степень с последующей проверкой полученных корней, а также методом сведения к равносильной системе уравнений и неравенств. Метод уединения радикала.
Литература для учителя:
Литература для ученика:
Занятие №4
Тема: Решение иррациональных уравнений методом замены.
Цель: Научить учащихся решать иррациональные уравнения методом замены.
Краткое содержание: Применение метода замены в случае, если в уравнении неоднократно встречается некоторое выражение. Решение иррациональных уравнений методом сведения к эквивалентным системам рациональных уравнений при помощи введения двух вспомогательных неизвестных.
Литература для учителя:
Литература для ученика:
Занятие №5
Тема: Применение рационализирующих подстановок при решении иррациональных уравнений.
Цель: Научить учащихся решать иррациональные уравнения при помощи рационализирующих подстановок.
Краткое содержание: Рассмотрение рационализации некоторых выражений, содержащих радикалы, с помощью рационализирующих подстановок и применение этих подстановок при решении иррациональных уравнений.
Литература для учителя:
Литература для ученика:
Занятие №6
Тема: Решение иррациональных уравнений функционально-графическим методом.
Цель: Научить учащихся решать иррациональные уравнения и неравенства, используя свойства входящих в них функций.
Краткое содержание: Использование ОДЗ, монотонности, графиков функций при решении иррациональных уравнений.
Литература для учителя:
Литература для ученика:
Занятие №7
Тема: Обобщение и систематизация методов решения иррациональных уравнений.
Цель:
1) Показать учащимся, что иррациональные уравнения можно решать не одним методом.
2) Систематизировать методы решения иррациональных уравнений.
3) Научить выбирать наиболее рациональный способ решения.
Краткое содержание: Рассмотрение различных методов решения на примере одного иррационального уравнения вида ![]() .
.
Литература для учителя:
Литература для ученика:
Занятие №8
Тема: Иррациональные уравнения, содержащие знак модуля или параметр. Решение уравнений смешанного типа.
Цель: Показать учащимся как решаются уравнения смешанного типа и уравнения, содержащие знак модуля и параметр.
Краткое содержание: Решение иррациональных уравнений с параметром и модулем, а также иррациональные уравнения, содержащие логарифмические, показательные или тригонометрические выражения.
Литература для учителя:
Литература для ученика:
Заключение
В данной работе сделана попытка разработать методику обучения решению иррациональных уравнений и неравенств в школе.
При проведении исследования были решены следующие задачи:
1) Проанализированы действующие учебники алгебры и начала математического анализа для выявления представленной в них методики решения иррациональных уравнений и неравенств. Проведенный анализ позволяет сделать следующие выводы:
·в средней школе недостаточное внимание уделяется методам решения различных иррациональных уравнений, в основном программой предусмотрено формирование у учащихся решать простейшие иррациональные уравнения и неравенства;
·в учебнике [1] материала, посвященного методам решения иррациональных уравнений нет. В остальных учебниках рассмотрены два основных способа решения: возведение обеих частей уравнения в степень, с последующей подстановкой полученных корней в исходное уравнение, а также решение уравнений с помощью равносильных преобразований;
·очень мало материала по методам решения иррациональных неравенств;
·среди предлагаемых заданий в учебниках много однотипных;
2) Изучена учебно-методическая литература по данной теме;
3) Рассмотрены основные методы и приемы решения различных иррациональных уравнений и неравенств;
4) Рассмотрены ситуации, связанные с потерей или приобретением посторонних корней в процессе решения, показано, как распознавать и предотвращать их;
5) Подобраны примеры решения иррациональных уравнений и неравенств для демонстрации излагаемого теоретического материала;
6) Разработана
Список библиографии
1. Алимов Ш. А. Алгебра и начала анализа [Текст]: учебник для 10-11 класса средней школы / Ш. А. Алимов – М.: Просвещение, 1993. – 254 с.
2. Башмаков М. И. Алгебра и начала анализа [Текст]: учебник для 10-11 класса средней школы / М. И. Башмаков – М.: Просвещение, 1992. – 351 с.
3. Болтянский В. Г. Математика: лекции, задачи, решения [Текст] / В. Г. Болтянский – Литва: Альфа, 1996. – 637 с.
4. Виленкин Н. Я. и др. Алгебра и математический анализ для 11 класса [Текст]: учебное пособие для учащихся школ и классов с углубленным изучением математики / Н. Я. Виленкин – М.: Просвещение, 1998. – 288 с.
5. Галицкий М. Л. Сборник задач по алгебре для 8-9 классов [Текст]: учебное пособие для учащихся школ и классов с углубленным изучением математики М. Л. Галицкий – М.: Просвещение, 1999. – 271с.
6. Григорьев А. М. Иррациональные уравнения [Текст] / А. М. Григорьев // Квант. – 1972. – №1. – С. 46-49.
7. Денищева Л. О. Готовимся к единому государственному экзамену. Математика. [Текст] / Л. О. Денищева – М.: Дрофа, 2004. – 120 с.
8. Егоров А. Иррациональные неравенства [Текст] / А Егоров // Математика. Первое сентября. – 2002. – №15. – С. 13-14.
9. Егоров А. Иррациональные уравнения [Текст] / А Егоров // Математика. Первое сентября – 2002. – №5. – С. 9-13.
10. Мордкович А. Г. Алгебра и начала анализа. 10-11 класс [Текст]: В двух частях. Ч.1: учебник для общеобразовательных учреждений / А. Г. Мордкович – М.: Мнемозина, 2004. – 315 с.
11. Мордкович А. Г. Алгебра и начала анализа. 10-11 класс [Текст]: В двух частях. Ч.2: задачник для общеобразовательных учреждений / А. Г. Мордкович – М.: Мнемозина, 2004. – 315 с.
12. Мордкович А. Г. Кто-то теряет, кто-то находит [Текст] / А. Г. Мордкович // Квант – 1970. – №5. – С. 48-51.
13. Колмогоров А. Н. Алгебра и начала анализа [Текст]: учебник для 10-11 класса средней школы / А. Н. Колмогоров – М.: Просвещение, 1991. – 320 с.
14. Кузнецова Г. М. Программа для общеобразовательных школ, гимназий, лицеев: Математика. 5-11 классы [Текст] / Г. М. Кузнецова – М.: Дрофа, 2004 – 320 с.
15. Потапов М. Как решать уравнения без ОДЗ [Текст] / М. Потапов // Математика. Первое сентября – 2003. – №21. – С. 42-43.
16. Соболь Б. В. Пособие для подготовки к единому государственному экзамену и централизованному тестированию по математике [Текст] / Б. В. Соболь – Ростов на Дону: Феникс, 2003. – 352 с.
17. Черкасов О. Ю. Математика [Текст]: справочник для старшеклассников и поступающих в вузы / О. Ю. Черкасов – М.: АСТ-ПРЕСС, 2001. – 576 с.
18. Шабунин М. Лекции для абитуриентов. Лекция 1. [Текст] / М. Шабунин // Математика. Первое сентября – 1996. – №24. – С. 24.
19. Шувалова Э. З. Повторим математику [Текст]: учебное пособие для поступающих в вузы / Э. З. Шувалова – М.: Высшая школа, 1974. – 519 с.
20. Моденов В. П. Решение иррациональных уравнений [Текст] / В. П. Моденов // Математика в школе – 1970. – №6. – С. 32-35.
21. Горнштейн П. И. Экзамен по математике и его подводные рифы [Текст] / П. И. Горнштейн – М.: Илекса, Харьков: Гимназия, 1998, – 236 с.
22. http://www.courier.com.ru
23. http://www.5ballov.ru.
24. Шарова Л. И. Уравнения и неравенства [Текст]: пособие для подготовительных отделений / Л. И. Шарова – Киев: Вища школа, 1981. – 280 с.
25. Олейних…
26. Егоров А. Иррациональные неравенства [Текст] / А Егоров // Математика. Первое сентября. – 2002. – №17. – С. 13-14.
27. Мордкович А. Г. Алгебра. 8 класс [Текст]: В двух частях. Ч.1: учебник для общеобразовательных учреждений / А. Г. Мордкович – М.: Мнемозина, 2004. – 315 с.
28. Мордкович А. Г. Алгебра. 8 класс [Текст]: В двух частях. Ч.2: задачник для общеобразовательных учреждений / А. Г. Мордкович – М.: Мнемозина, 2003. – 239 с.
Приложение А
Решение иррациональных уравнений смешанного типа
Для каждого вида уравнений и неравенств, в том числе и иррациональных, можно составить уравнение или неравенство «с модулем» и «с параметром».
Иррациональные уравнения, содержащие знак модуля
Простейшие уравнения с модулем имеют вид: ![]() и
и ![]() ; будем их решать на основании определения модуля сведением к совокупности систем.
; будем их решать на основании определения модуля сведением к совокупности систем.
 Пример 1. Решить уравнение
Пример 1. Решить уравнение ![]() .
.
Решение. ![]() ,
,
Данное уравнение равносильно совокупности двух систем:
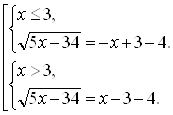
Будем решать каждую из систем по отдельности.
Решение первой системы:
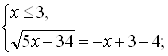
![]()
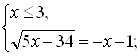
![]()
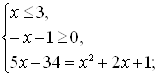
![]()
![]()
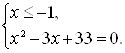
Последняя система не имеет корней, так как дискриминант уравнения ![]() меньше нуля.
меньше нуля.
Решение второй системы:
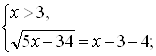
![]()

![]()
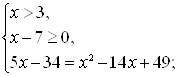
![]()
![]()
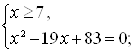
![]()
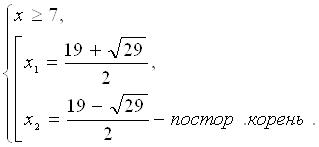
Ответ: ![]() .
.
 Пример 2. Решить уравнение
Пример 2. Решить уравнение ![]()
Решение. ![]() ,
,
Данное уравнение равносильно совокупности двух систем:

Будем решать каждую из систем по отдельности.
Решение первой системы:
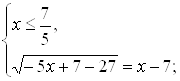
![]()
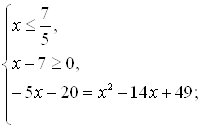
![]()
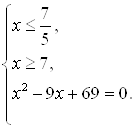
Если внимательно посмотреть на неравенства последней системы, можно заметить, что пересечение множеств 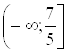 и
и ![]() пусто. Следовательно, первая система совокупности корней не имеет.
пусто. Следовательно, первая система совокупности корней не имеет.
Решение второй системы:

![]()
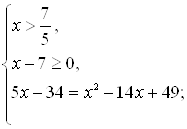
![]()
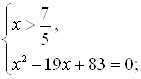
![]()
![]()
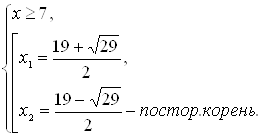
Ответ: ![]() .
.
Иррациональные уравнения, содержащие параметр
Уравнение вида ![]() называется иррациональным с параметром относительно неизвестного
называется иррациональным с параметром относительно неизвестного ![]() , если одна или обе его части содержат выражения, иррациональные относительно
, если одна или обе его части содержат выражения, иррациональные относительно ![]() .
.
Как и раньше, будем находить только действительные корни.
Трудно указать какой-нибудь общий и вместе с тем достаточно простой способ решения иррациональных уравнений, содержащих параметр.
Проиллюстрируем некоторые способы решения на примерах.
Пример 3. Для каждого действительного значения параметра ![]() решить уравнение
решить уравнение
![]() .
.
Решение. Исходное уравнение равносильно смешанной системе
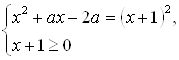
![]()
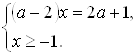
При ![]() эта система решений не имеет.
эта система решений не имеет.
При ![]() получим решение
получим решение
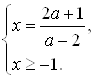
Теперь необходимо найти те значения ![]() , при которых эта система имеет решение:
, при которых эта система имеет решение:
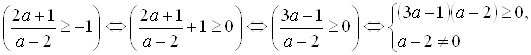
![]()
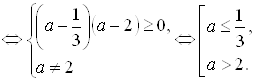
Ответ: при ![]() – корней нет;
– корней нет;
при 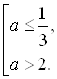
![]() .
.
Для решения иррационального уравнения иногда удобно ввести вспомогательную неизвестную величину. При этом получаем квадратное уравнение с параметром, которое нужно решить в пределах некоторого ограниченного множества значений нового неизвестного.
Пример 4. Решить уравнение ![]() .
.
Решение. Область определения данного уравнения:
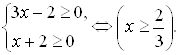
Так как ![]() и
и ![]() , то и
, то и ![]() .
.
Сделаем замену ![]()
![]() , тогда
, тогда ![]() и исходное уравнение можно записать в виде системы
и исходное уравнение можно записать в виде системы
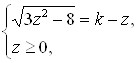
которая равносильна системе
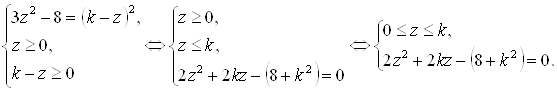
Корни уравнения ![]() должны удовлетворять первому условию последней системы, то есть необходимо решить систему
должны удовлетворять первому условию последней системы, то есть необходимо решить систему

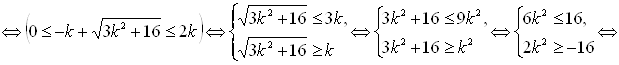

Итак, при 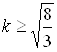 исходное уравнение имеет единственный корень
исходное уравнение имеет единственный корень ![]() . Отсюда при
. Отсюда при 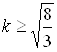 имеем
имеем
![]() ,
,
![]()
Ответ: при 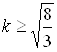
![]() ;
;
при 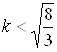 – корней нет.
– корней нет.
Иррациональные показательные уравнения
Пример 5. Решить уравнение ![]() .
.
Решение. Перепишем уравнение так:
![]() ,
,
Приведем все степени к одному основанию 7:
![]() .
.
Сделаем замену ![]() ,
, ![]() , тогда получаем уравнение
, тогда получаем уравнение ![]() , корнями которого являются
, корнями которого являются ![]()
![]()
Сделаем обратную замену:
|
|
|
Ответ: ![]() .
.
Пример 6. Решить уравнение ![]() .
.
Решение. Приведем все степени к одному основанию:
![]()
![]()
![]()
![]()
![]() .
.
откуда получаем уравнение ![]() которое равносильно уравнению:
которое равносильно уравнению:
![]()
![]()
![]()
Ответ: ![]()
Иррациональные логарифмические уравнения
Пример 7. Решить уравнение ![]() .
.
Решение. Преобразуем данное уравнение:
![]() .
.
Учитывая ОДЗ, данное уравнение равносильно системе:
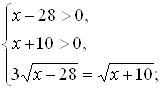
![]()
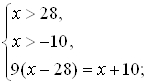
![]()
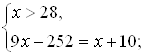
![]()
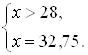
Ответ: ![]()
Пример 8. Решить уравнение
![]()
Решение. Учитывая ОДЗ, данное уравнение равносильно системе:
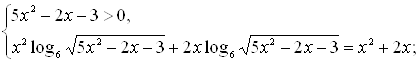
![]()
![]()
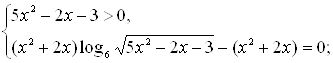
![]()
![]()
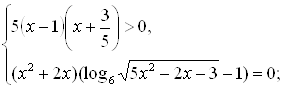
Уравнение этой системы равносильно совокупности уравнений:
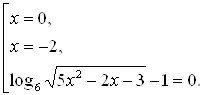
Последнее уравнение этой совокупности равносильно уравнению:
![]()

Из неравенства системы 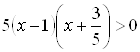 следует, что
следует, что 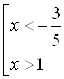 . Следовательно,
. Следовательно, ![]() – посторонний корень.
– посторонний корень.
Ответ: ![]() ,
, ![]()
Сколько корней имеет уравнение ![]() ?
?
Сколько корней имеет уравнение ![]() ?
?
Приложение Б
Диагностирующая контрольная работа №1
| 1. Сколько корней имеет уравнение | |||
| А. ни одного | Б. один | В. два | Г. четыре |
| 2. Решите уравнение | |||
| А. | Б. 1 | В. 2 | Г. корней нет |
| 3. Укажите промежуток, которому принадлежит корень уравнения | |||
| А. | Б. | В. | Г. |
| 4. Решите уравнение | |||
| 5. Решите уравнение | |||
| 6. Решите уравнение | |||
| 7. Решите уравнение | |||
| 8. Решите уравнение | |||
Диагностирующая контрольная работа №2
| 1. Сколько корней имеет уравнение | |||
| А. четыре | Б. два | В. один | Г. ни одного |
| 2. Решите уравнение | |||
| А. 4 | Б. 1 | В. | Г. корней нет |
| 3. Укажите промежуток, которому принадлежит корень уравнения | |||
| А. | Б. | В. | Г. |
| 4. Решите уравнение | |||
| 5. Решите уравнение | |||
| 6. Решите уравнение | |||
| 7. Решите уравнение | |||
| 8. Решите уравнение | |||
Ответы и решение заданий диагностирующей контрольной работы №1
1. А.
2. А.
3. Б.
4. Уединив первый радикал, получаем уравнение ![]() , равносильное исходному. Возводя обе части этого уравнения в квадрат, получаем уравнение
, равносильное исходному. Возводя обе части этого уравнения в квадрат, получаем уравнение![]() ,
, ![]()
![]() . Последнее уравнение равносильно системе
. Последнее уравнение равносильно системе 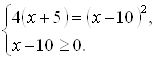 Решая уравнение этой системы, равносильное уравнению
Решая уравнение этой системы, равносильное уравнению ![]() , получим корни
, получим корни ![]() и
и ![]() . Первый корень не удовлетворяет неравенству системы и, следовательно, является посторонним корнем исходного уравнения. Ответ:
. Первый корень не удовлетворяет неравенству системы и, следовательно, является посторонним корнем исходного уравнения. Ответ: ![]() .
.
5. Введем новую переменную 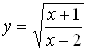 , тогда
, тогда 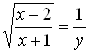 , причем
, причем ![]() . В результате исходное иррациональное уравнение принимает вид квадратного
. В результате исходное иррациональное уравнение принимает вид квадратного 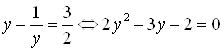 , откуда учитывая ограничение
, откуда учитывая ограничение ![]() , получаем
, получаем ![]() . Решая уравнение
. Решая уравнение 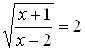 , получаем корень
, получаем корень ![]() . Как показывает проверка,
. Как показывает проверка, ![]() удовлетворяет исходному уравнению. Ответ:
удовлетворяет исходному уравнению. Ответ: ![]() .
.
6. Введем новую переменную ![]() . В результате исходное иррациональное уравнение принимает вид
. В результате исходное иррациональное уравнение принимает вид 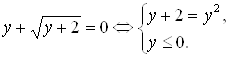 Решая первое уравнение этой системы, получим корни
Решая первое уравнение этой системы, получим корни ![]() и
и ![]() . Второй корень не удовлетворяет неравенству системы. Решая уравнение
. Второй корень не удовлетворяет неравенству системы. Решая уравнение ![]() , получаем корни
, получаем корни ![]() и
и ![]() . Как показывает проверка, оба корня удовлетворяют исходному уравнению. В ответе нужно указать наибольший из корней. Ответ:
. Как показывает проверка, оба корня удовлетворяют исходному уравнению. В ответе нужно указать наибольший из корней. Ответ: ![]() .
.
7. Данное уравнение равносильно совокупности двух систем: 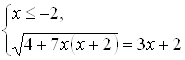 и
и 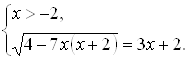 Будем решать каждую из систем по отдельности. Решение первой системы:
Будем решать каждую из систем по отдельности. Решение первой системы: 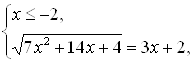
![]()
![]()
 Если внимательно посмотреть на неравенства последней системы, можно заметить, что пересечение множеств
Если внимательно посмотреть на неравенства последней системы, можно заметить, что пересечение множеств ![]() и
и 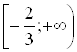 пусто. Следовательно, первая система совокупности корней не имеет. Решение второй системы:
пусто. Следовательно, первая система совокупности корней не имеет. Решение второй системы: 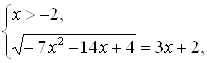
![]()

![]()
![]()
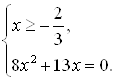 Решая уравнение этой системы, равносильное уравнению
Решая уравнение этой системы, равносильное уравнению ![]() , получим корни
, получим корни ![]() и
и ![]() . Второй корень не удовлетворяет неравенству системы и, следовательно, является посторонним корнем исходного уравнения. Ответ:
. Второй корень не удовлетворяет неравенству системы и, следовательно, является посторонним корнем исходного уравнения. Ответ: ![]() .
.
8. Введем новые переменные ![]() и
и ![]() . Тогда исходное уравнение принимает вид:
. Тогда исходное уравнение принимает вид: ![]() . Поскольку мы ввели две новые неизвестные, надо найти еще одно уравнение, связывающее y и z. Для этого возведем равенства
. Поскольку мы ввели две новые неизвестные, надо найти еще одно уравнение, связывающее y и z. Для этого возведем равенства ![]() ,
, ![]() в третью степень и заметим, что
в третью степень и заметим, что ![]() . Итак, надо решить систему уравнений
. Итак, надо решить систему уравнений 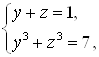 она имеет два (действительных) решения:
она имеет два (действительных) решения: ![]() ,
, ![]() ;
; ![]() ,
, ![]() . Остается решить систему двух уравнений с одним неизвестным
. Остается решить систему двух уравнений с одним неизвестным 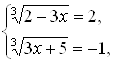 и систему
и систему 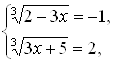 первая из них дает
первая из них дает ![]() , вторая дает
, вторая дает ![]() . Как показывает проверка, оба корня удовлетворяют исходному уравнению. Ответ:
. Как показывает проверка, оба корня удовлетворяют исходному уравнению. Ответ: ![]() ,
, ![]() .
.
Ответы и решение заданий диагностирующей контрольной работы №2
1. Б.
2. В.
3. Г.
4. Уединив первый радикал, получаем уравнение ![]() , равносильное исходному. Возводя обе части этого уравнения в квадрат, получаем уравнение
, равносильное исходному. Возводя обе части этого уравнения в квадрат, получаем уравнение![]() ,
,![]()
![]() . Последнее уравнение равносильно системе
. Последнее уравнение равносильно системе 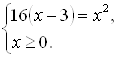 Решая уравнение этой системы, равносильное уравнению
Решая уравнение этой системы, равносильное уравнению ![]() , получим корни
, получим корни ![]() и
и ![]() . Оба корня удовлетворяют неравенству системы и, следовательно, являются корнями исходного уравнения. В ответе нужно указать произведение корней. Ответ: 48.
. Оба корня удовлетворяют неравенству системы и, следовательно, являются корнями исходного уравнения. В ответе нужно указать произведение корней. Ответ: 48.
5. Введем новую переменную 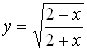 , тогда
, тогда 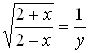 , причем
, причем ![]() . В результате исходное иррациональное уравнение принимает вид квадратного
. В результате исходное иррациональное уравнение принимает вид квадратного 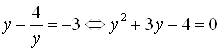 , откуда учитывая ограничение
, откуда учитывая ограничение ![]() , получаем
, получаем ![]() . Решая уравнение
. Решая уравнение 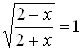 , получаем корень
, получаем корень ![]() . Как показывает проверка,
. Как показывает проверка, ![]() удовлетворяет исходному уравнению. Ответ:
удовлетворяет исходному уравнению. Ответ: ![]() .
.
6. Введем новую переменную ![]() . В результате исходное иррациональное уравнение принимает вид
. В результате исходное иррациональное уравнение принимает вид ![]()
![]()
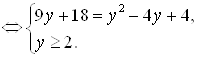 Решая первое уравнение этой системы, равносильное уравнению
Решая первое уравнение этой системы, равносильное уравнению ![]() , получим корни
, получим корни ![]() и
и ![]() . Первый корень не удовлетворяет неравенству системы. Решая уравнение
. Первый корень не удовлетворяет неравенству системы. Решая уравнение ![]() , получаем корни
, получаем корни ![]() и
и ![]() . Как показывает проверка, оба корня удовлетворяют исходному уравнению. В ответе нужно указать наибольший из корней. Ответ:
. Как показывает проверка, оба корня удовлетворяют исходному уравнению. В ответе нужно указать наибольший из корней. Ответ: ![]() .
.
7. Данное уравнение равносильно совокупности двух систем:  и
и 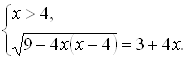 Будем решать каждую из систем по отдельности. Решение первой системы:
Будем решать каждую из систем по отдельности. Решение первой системы: 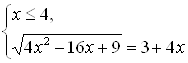
![]()
![]()

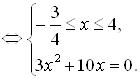 Решая уравнение этой системы, равносильное уравнению
Решая уравнение этой системы, равносильное уравнению ![]() , получим корни
, получим корни ![]() и
и ![]() . Второй корень не удовлетворяет неравенству системы и, следовательно, является посторонним корнем исходного уравнения. Решение второй системы:
. Второй корень не удовлетворяет неравенству системы и, следовательно, является посторонним корнем исходного уравнения. Решение второй системы: 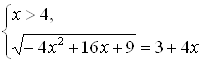
![]()

![]()
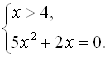 Решая уравнение этой системы, равносильное уравнению
Решая уравнение этой системы, равносильное уравнению ![]() , получим корни
, получим корни ![]() и
и ![]() . Оба корня не удовлетворяют неравенству системы и, следовательно, являются посторонними корнями исходного уравнения. Ответ:
. Оба корня не удовлетворяют неравенству системы и, следовательно, являются посторонними корнями исходного уравнения. Ответ: ![]() .
.
8. Введем новые переменные ![]() и
и ![]() . Тогда исходное уравнение принимает вид:
. Тогда исходное уравнение принимает вид: ![]() . Поскольку мы ввели две новые неизвестные, надо найти еще одно уравнение, связывающее y и z. Для этого возведем равенства
. Поскольку мы ввели две новые неизвестные, надо найти еще одно уравнение, связывающее y и z. Для этого возведем равенства ![]() ,
, ![]() в четвертую степень и заметим, что
в четвертую степень и заметим, что ![]() . Итак, надо решить систему уравнений
. Итак, надо решить систему уравнений 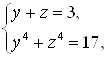 она имеет два (действительных) решения:
она имеет два (действительных) решения: ![]() ,
, ![]() ;
; ![]() ,
, ![]() . Остается решить систему двух уравнений с одним неизвестным
. Остается решить систему двух уравнений с одним неизвестным 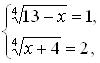 и систему
и систему 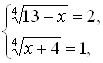 первая из них дает
первая из них дает ![]() , вторая дает
, вторая дает ![]() . Как показывает проверка, оба корня удовлетворяют исходному уравнению. Ответ:
. Как показывает проверка, оба корня удовлетворяют исходному уравнению. Ответ: ![]() ,
, ![]() .
.
Приложение В
Разработка факультативного занятия на тему «Способ рационализации при решении иррациональных уравнений»
Ход занятия
Иногда посредством некоторой подстановки удается привести иррациональное уравнение к рациональному виду. В таком случае говорят, что эта подстановка рационализирует рассматриваемое иррациональное уравнение, и называют ее рационализирующей.
Способ решения иррациональных уравнений, основанный на применении рационализирующих подстановок, назовем способом рационализации.
Применяя рационализирующую подстановку, необходимо следить за тем, чтобы область определения нового рационального уравнения, получаемого в результате этой подстановки, соответствовала области определения данного иррационального уравнения. Только при этом условии рационализирующая подстановка приведет рассматриваемое иррациональное уравнение к рациональному уравнению, которое всюду в области его определения эквивалентно данному.
Рассмотрим рационализацию некоторых выражений, содержащих радикалы, с помощью рационализирующих подстановок и применение этих подстановок при решении иррациональных уравнений.
1. Рационализация выражения ![]()
Выражение вида
![]() , (1)
, (1)
где ![]() обозначает рациональную функцию,
обозначает рациональную функцию, ![]() и
и ![]() – постоянные, а
– постоянные, а ![]() – любое целое положительное число, рационализируется подстановкой
– любое целое положительное число, рационализируется подстановкой
![]() . (2)
. (2)
Действительно, возводя обе части равенства (2) в ![]() -ую степень, получим
-ую степень, получим ![]() , откуда
, откуда ![]() , причем функция
, причем функция ![]() рациональна. Следовательно,
рациональна. Следовательно,
![]() .
.
Поскольку рациональная функция от рациональной функции представляет собой также рациональную функцию, то выражение, стоящее в правой части последнего равенства, является рациональным.
Пример 1. Решить уравнение ![]() .
.
Решение. ОДЗ рассматриваемого уравнения ![]() . Рационализирующей подстановкой
. Рационализирующей подстановкой ![]()
![]() это уравнение приводится к эквивалентной ему смешанной системе
это уравнение приводится к эквивалентной ему смешанной системе
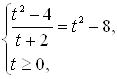
или (сокращая дробь на ![]() ) системе
) системе
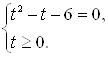
Решением последней будет ![]()
![]() . Воспользовавшись подстановкой, получим
. Воспользовавшись подстановкой, получим ![]() .
.
Ответ: ![]() .
.
Похожие работы
... на основе знания связи между результатом и компонентами арифметических действий (т.е. знания способов нахождения неизвестных компонентов). Эти требования программы определяют методику работы над уравнениями. 2. Методика изучения неравенств в старших классах 2.1 Содержание и роль линии уравнений и неравенств в современном школьном курсе математики Ввиду важности и обширности материала, ...
... на качественно новую ступень овладения содержанием школьной математики. Глава II. Методико - педагогические основы использования самостоятельной работы, как средство обучения решению уравнений в 5 - 9 классах. § 1. Организация самостоятельной работы при обучения решению уравнений в 5 - 9 классах. При традиционном способе преподавания учитель часто ставит ученика в положение объекта ...
... , можно сделать вывод о недостаточном освещении изучаемого вопроса в современной методической литературе. Объект исследования работы: процесс обучения математике. Предмет: формирование умения решения квадратных уравнений у учащихся 8-го класса. Контингент: учащиеся 8-го класса. Глава 1. Теоретические аспекты обучению решения уравнений в 8 классе 1.1. Из истории возникновения квадратных ...
... числового аргумента, поэтому при таком подходе наблюдается определённая избыточность в формировании функции как обобщённого понятия. 2. Основные направления введения понятия функции в школьном курсе математики В современном школьном курсе математики ведущим подходом считается генетический с добавлением элементов логического. Формирование понятий и представлений, методов и приёмов в составе ...
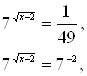 или
или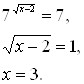
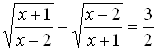 , укажите корень уравнения.
, укажите корень уравнения.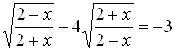 , укажите корень уравнения.
, укажите корень уравнения.
0 комментариев