Навигация
Рациональность дробно-линейных иррациональностей
2. Рациональность дробно-линейных иррациональностей
Аналогично предыдущему доказывается, что функция вида
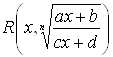 , (3)
, (3)
где ![]() ,
, ![]() ,
, ![]() и
и ![]() – некоторые постоянные, а
– некоторые постоянные, а ![]() – любое целое положительное число (дробно-линейная иррациональность), может быть при условии
– любое целое положительное число (дробно-линейная иррациональность), может быть при условии ![]() приведена к рациональному виду подстановкой
приведена к рациональному виду подстановкой
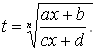 (4)
(4)
Иррациональная функция
 (5)
(5)
рационализируется при помощи подстановки
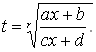 (6)
(6)
где ![]() – наименьшее общее кратное показателей радикалов
– наименьшее общее кратное показателей радикалов ![]() ,
, ![]() , …
, …
Пример 2. Решить уравнение ![]() .
.
Решение. Будем искать корни данного уравнения в области ![]() (очевидно, что числа
(очевидно, что числа ![]() и
и ![]() не являются его корнями). Разделим обе части уравнения на
не являются его корнями). Разделим обе части уравнения на ![]() :
:
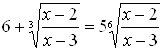 .
.
Полученное уравнение в рассматриваемой области с помощью рационализирующей подстановки
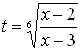
![]()
сводится к смешанной системе
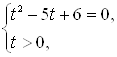
эквивалентной ему в этой области. Определив решения этой системы ![]() и
и ![]() и воспользовавшись подстановкой, находим корни исходного уравнения.
и воспользовавшись подстановкой, находим корни исходного уравнения.
Ответ: ![]() .
.
3. Рационализация биноминальных выражений
Можно доказать, что выражение
![]() ,
(7)
,
(7)
где ![]() и
и ![]() – постоянные, а показатели степеней
– постоянные, а показатели степеней ![]() ,
, ![]() – некоторые рациональные числа, допускает рационализирующие подстановки только в трех случаях, когда оказывается целым одно из чисел
– некоторые рациональные числа, допускает рационализирующие подстановки только в трех случаях, когда оказывается целым одно из чисел ![]() ,
, ![]() или
или ![]() .
.
В этих случаях возможны следующие подстановки:
Если ![]() – целое, то
– целое, то ![]() , где
, где ![]() – наименьшее общее кратное знаменателей чисел
– наименьшее общее кратное знаменателей чисел ![]() и
и ![]() .
.
Если ![]() – целое, то
– целое, то ![]() , где
, где ![]() – знаменатель числа
– знаменатель числа ![]() .
.
Если ![]() – целое, то
– целое, то 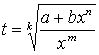 , где
, где ![]() – знаменатель числа
– знаменатель числа ![]() .
.
Существование указанных трех рационализирующих подстановок доказывает возможность приведения к рациональному виду уравнений ![]() в первом случае и
в первом случае и ![]() во втором и третьем случаях.
во втором и третьем случаях.
Пример 3. Решить уравнение ![]() .
.
Решение. Так как ![]() – не является корнем уравнения, разделим обе его части на
– не является корнем уравнения, разделим обе его части на ![]() . Выделяется биномиальное выражение:
. Выделяется биномиальное выражение:
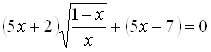 .
.
Имеет место третий случай рационализации (![]() и
и ![]() – целое число). Следовательно, будем применять подстановку
– целое число). Следовательно, будем применять подстановку 
![]() . Возводя обе части этого равенства в квадрат, получим
. Возводя обе части этого равенства в квадрат, получим ![]() , так что
, так что ![]() . Теперь с помощью подстановки
. Теперь с помощью подстановки  и найденного значения
и найденного значения ![]() получаем
получаем
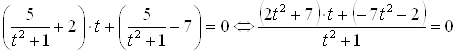
и исходное иррациональное уравнение приводится к рациональному ![]() , или
, или 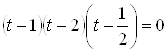 . Определив корни этого уравнения
. Определив корни этого уравнения ![]()
![]() ,
, ![]() и воспользовавшись подстановкой, находим
и воспользовавшись подстановкой, находим ![]()
Ответ: ![]()
Похожие работы
... на основе знания связи между результатом и компонентами арифметических действий (т.е. знания способов нахождения неизвестных компонентов). Эти требования программы определяют методику работы над уравнениями. 2. Методика изучения неравенств в старших классах 2.1 Содержание и роль линии уравнений и неравенств в современном школьном курсе математики Ввиду важности и обширности материала, ...
... на качественно новую ступень овладения содержанием школьной математики. Глава II. Методико - педагогические основы использования самостоятельной работы, как средство обучения решению уравнений в 5 - 9 классах. § 1. Организация самостоятельной работы при обучения решению уравнений в 5 - 9 классах. При традиционном способе преподавания учитель часто ставит ученика в положение объекта ...
... , можно сделать вывод о недостаточном освещении изучаемого вопроса в современной методической литературе. Объект исследования работы: процесс обучения математике. Предмет: формирование умения решения квадратных уравнений у учащихся 8-го класса. Контингент: учащиеся 8-го класса. Глава 1. Теоретические аспекты обучению решения уравнений в 8 классе 1.1. Из истории возникновения квадратных ...
... числового аргумента, поэтому при таком подходе наблюдается определённая избыточность в формировании функции как обобщённого понятия. 2. Основные направления введения понятия функции в школьном курсе математики В современном школьном курсе математики ведущим подходом считается генетический с добавлением элементов логического. Формирование понятий и представлений, методов и приёмов в составе ...
0 комментариев