Навигация
Общие правила минимизации
3.12.2.1.1 Общие правила минимизации
Минимизацию можно проводить по единицам (нулям). При этом:
1) Смежные единицы (нули) диаграммы условно охватывают (накрывают) прямоугольными контурами. Каждый контур может содержать 2,4,8,16, ... единиц (нулей).
2) Одним контуром (накрытием) необходимо объединить максимальное количество смежных клеток, содержащих единицы (нули).
3) Необходимо, чтобы каждая единица (нуль) накрывалась хотя бы один раз.
4) Одна и та же единица (нуль) может охватываться несколько раз разными контурами.
5) Верхняя и нижняя строки диаграммы считаются смежными - их можно представить таковыми, если мысленно свернуть диаграмму в горизонтальный цилиндр.
6) Левый и правый столбцы также считаются смежными - диаграмму можно мысленно свернуть в вертикальный цилиндр.
7) Угловые клетки также считаются смежными - диаграмму можно мысленно свернуть в тор.
8) Перед выполнением минимизации в клетки, содержащие прочерки (на данных наборах ПФ неопределена), можно записать дополнительные единицы (нули), что способствует получению более простого конечного булевого выражения. При этом следует помнить, что хотя бы один раз необходимо накрыть лишь основные единицы (нули). Дополнительные единицы (нули) могут увеличивать суммарное число единиц (нулей), входящих в накрытие, а, следовательно, уменьшать число переменных в результирующих конъюнкциях (дизъюнкциях).
9) Результатом минимизации является булево выражение в ДНФ (КНФ). Количество конъюнкций в ДНФ (дизъюнкций в КНФ) соответствует числу контуров (накрытий).
10) В каждую конъюнкцию (дизъюнкцию) войдут только те переменные, значение которых в пределах контура не меняется (переменная принимает в накрытии только единичное или нулевое значение (входит только в прямой или инверсной форме)).
При минимизации по единицам в результирующие конъюнкции переменные входят в прямой форме, если соответствующие им строки и столбцы диаграммы помечены чертой. Переменные, связанные со строками и столбцами, не помеченными чертой, входят в конъюнкции в инверсной форме.
При минимизации по нулям в результирующие дизъюнкции переменные входят в прямой форме, если соответствующие им строки и столбцы не помечены чертой, в противном случае дизъюнкции содержат переменные в инверсном виде.
Целью минимизации является получение минимальной ДНФ или КНФ, содержащей минимум членов с минимальным количеством входящих в них переменных. Для этого необходимо минимальным числом контуров охватить хотя бы один раз каждую единицу (нуль). При этом необходимо стремиться, чтобы в каждое накрытие входило как можно больше смежных единиц (нулей).
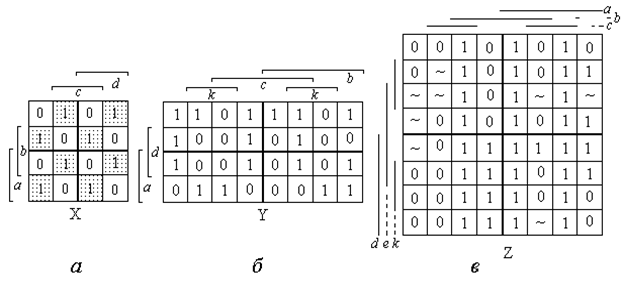
На рисунке 3.1 показаны диаграммы Вейча при числе логических переменных n=2,3,4. Для n>4 диаграммы содержатся в [18]. Если наборы переменных исходной таблицы истинности упорядочены по убыванию их десятичных эквивалентов, то следует воспользоваться диаграммами Вейча, приведенными в [5, 6]
3.12.2.1.2 Примеры минимизации ПФ с помощью диаграмм Вейча
Пример 1. Для контроля за возможной деформацией металлической конструкции из-за перегрева в ее различных критических точках установлены четыре термодатчика, обозначенные ТД1, ТД2, ТД3, ТД4. Экспериментальные исследования конструкции показали, что в процессе ее эксплуатации возможны шесть сочетаний сработавших и не сработавших датчиков. При этом деформация конструкции возникала в следующих случаях:
1) сработали ТД4, ТД3 и не сработали ТД2 и ТД1;
2) сработали ТД4, ТД3, ТД2 и ТД1;
3) сработали ТД2 и не сработали ТД4, ТД3 и ТД1;
4) сработали ТД3, ТД2 и ТД1 и не сработал ТД4;
В случаях, когда:
5) сработали ТД4, ТД3, ТД2 и не сработал ТД1;
6) сработали ТД2, ТД1 и не сработали ТД4, ТД3
деформация конструкции не возникала.
Таблица 3.5
| № | Состояние датчиков | Деформация конструкции | |
| Сработали | Не сработали | ||
| 1 | ТД4, ТД3 | ТД2, ТД1 | Возникала |
| 2 | ТД4 ... ТД1 | ― | |
| 3 | ТД2 | ТД4, ТД3, ТД1 | |
| 4 | ТД3, ТД2, ТД1 | ТД4 | |
| 5 | ТД4, ТД3, ТД2 | ТД1 | Не возникала |
| 6 | ТД2, ТД1 | ТД4, ТД3 | |
По условию эксплуатации конструкции другие сочетания сработавших и не сработавших датчиков невозможны.
Необходимо спроектировать цифровое логическое устройство, включающее сигнал тревоги, если происходит срабатывание термодатчиков в опасном сочетании.
Обозначим цифровые сигналы на выходе термодатчиков логическими переменными: ТД4→D; ТД3→С; ТД2→В; ТД1→А, а логическую функцию, которую должно реализовать устройство контроля – F.
Составим таблицу истинности, отражающую требуемую логическую функцию (таблица 3.6).
Таблица 3.6
|
| (ТД4) | (ТД3) | (ТД2) | (ТД1) |
|
|
| № набора | D | C | B | A | F |
|
| 0 | 0 | 0 | 0 | 0 | - |
|
| 1 | 0 | 0 | 0 | 1 | - |
|
| 2 | 0 | 0 | 1 | 0 | 1 | 3) |
| 3 | 0 | 0 | 1 | 1 | 0 | 6) |
| 4 | 0 | 1 | 0 | 0 | - |
|
| 5 | 0 | 1 | 0 | 1 | - |
|
| 6 | 0 | 1 | 1 | 0 | - |
|
| 7 | 0 | 1 | 1 | 1 | 1 | 4) |
| 8 | 1 | 0 | 0 | 0 | - |
|
| 9 | 1 | 0 | 0 | 1 | - |
|
| 10 | 1 | 0 | 1 | 0 | - |
|
| 11 | 1 | 0 | 1 | 1 | - |
|
| 12 | 1 | 1 | 0 | 0 | 1 | 1) |
| 13 | 1 | 1 | 0 | 1 | - |
|
| 14 | 1 | 1 | 1 | 0 | 0 | 5) |
| 15 | 1 | 1 | 1 | 1 | 1 | 2) |
Диаграмма Вейча, отражающая данную таблицу, показана на рисунке 3.2.
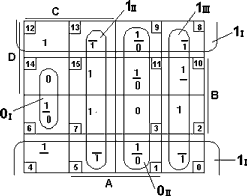
Рисунок 3.2
Если будем производить минимизацию по единицам, то в клетки, содержащие прочерки проставим дополнительные единицы.
Основные единицы накрываем тремя контурами: 1-й контур (1I) образуют клетки первой и последней строки, 2-й (1II) - клетки 2-го столбца и 3-й (1III) - 4-го столбца.
Итоговое булево выражение минимизированной ПФ имеет вид
![]() .(3.9)
.(3.9)
Это выражение должно быть реализовано цифровым логическим устройством, включающим сигнал тревоги.
Рассматриваемую функцию можно минимизировать и по нулевым значениям (нулям). Для этого доопределяем клетки с номерами 1,6,9 и 11 нулями и накрываем два основных нуля двумя прямоугольниками, включающими два и четыре элемента (нуля). Первый прямоугольник (0I) охватывает клетки с номерами 6,14, второй (0II) – 1,3,11 и 9.
Итоговое булево выражение минимизированной ПФ имеет вид
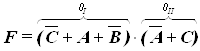 .(3.10)
.(3.10)
Оба выражения (3.9) и (3.10) эквивалентны, и применять следует то из них, которое проще реализуется на конкретном наборе логических элементов (базисе). Этот вопрос будет рассмотрен в следующих лекциях.
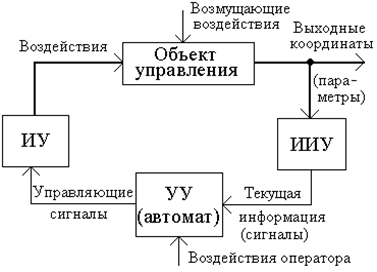
Пример 2. Необходимо разработать блок приоритетных прерываний от 2-х внешних устройств: ВУ1 и ВУ2. ВУ с меньшим номером соответствует более высокий приоритет. Упрощенная структура проектируемой системы показана на рисунке 3.3.
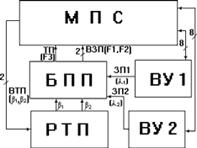
Рисунок 3.3
На схеме приняты следующие сокращения: МПС – микропроцессорная система; ВУ – внешнее устройство; БПП – блок приоритетных прерываний; ВТП – вектор текущего прерывания, который с помощью логических переменных β1, β2 описывает возможные состояния МП-системы при обслуживании запросов прерываний от ВУ (таблица 3.7); РТП – регистр текущего прерывания (запоминает значения переменных β1, β2); ЗП1, ЗП2 – запросы прерываний от ВУ1, ВУ2 (описываются переменными α1, α2); ТП – требование прерывания (логическая функция F3); ВЗП – вектор запроса прерывания (отображается комбинацией значений логических функций F1 и F2 (таблица 3.8)).
Таблица 3.7
| № набора | β1 | β2 | ВТП |
| 0 | 0 | 0 | ожидание |
| 1 | 0 | 1 | обслуживается ВУ1 |
| 2 | 1 | 0 | обслуживается ВУ2 |
| 3 | 1 | 1 | – |
Таблица 3.8
| ВЗП | F1 | F2 |
| F3 =0 или неопределено | – | – |
| Запрос от ВУ2 | 1 | 0 |
| Запрос от ВУ1 | 0 | 1 |
МП-система периодически проверяет значение сигнала ТП (функция F3). Если ТП=0 (запрос на прерывание отсутствует), то значения функций F1, F2 безразличны и МПС продолжает свою работу. Если ТП=1, то МП-система анализирует значение вектора ВЗП (комбинацию функций F1, F2) и определяет номер запроса прерывания. Так как набор переменных β1=β2=1 невозможен (таблица 3.6), то функции F1, F2, F3 в таких случаях неопределены. Таким образом, задача БПП является реализация трех логических функций F1, F2, F3, каждая из которых определяется значениями четырех логических переменных: α1, α2, β1и β2.
Составим таблицу истинности (таблица 3.9) для названных функций.
Таблица 3.9
|
| D | C | B | A |
|
|
|
| № набора | α1 | α2 | β1 | β2 | F3 | F1 | F2 |
| 0 | 0 | 0 | 0 | 0 | 0 | - | - |
| 1 | 0 | 0 | 0 | 1 | 0 | - | - |
| 2 | 0 | 0 | 1 | 0 | 0 | - | - |
| 3 | 0 | 0 | 1 | 1 | - | - | - |
| 4 | 0 | 1 | 0 | 0 | 1 | 1 | 0 |
| 5 | 0 | 1 | 0 | 1 | 0 | - | - |
| 6 | 0 | 1 | 1 | 0 | 0 | - | - |
| 7 | 0 | 1 | 1 | 1 | - | - | - |
| 8 | 1 | 0 | 0 | 0 | 1 | 0 | 1 |
| 9 | 1 | 0 | 0 | 1 | 0 | - | - |
| 10 | 1 | 0 | 1 | 0 | 1 | 0 | 1 |
| 11 | 1 | 0 | 1 | 1 | - | - | - |
| 12 | 1 | 1 | 0 | 0 | 1 | 0 | 1 |
| 13 | 1 | 1 | 0 | 1 | 0 | - | - |
| 14 | 1 | 1 | 1 | 0 | 1 | 0 | 1 |
| 15 | 1 | 1 | 1 | 1 | - | - | - |
Представляем функции F1, F2, F3 диаграммами Вейча (рисунок 3.4)
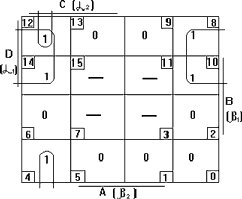
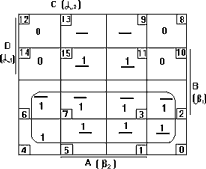
Для F3 Для F1
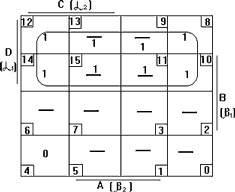
Для F2
Рисунок 3.4
Булевы выражения минимизированных ПФ имеют вид:
F3=![]() .(3.11)
.(3.11)
F1=![]() .(3.12)
.(3.12)
F2=![]() .(3.13)
.(3.13)
Полученные выражения (3.11-3.13) имеют вполне конкретное логическое толкование и при наличии определенных навыков могли быть получены без составления таблицы истинности и минимизации ПФ.
Так, если F3=1, а в противном случае F1 и F2 безразличны, то запрос от ВУ1 в виде комбинации F1=0, F2=1 поступит лишь тогда, когда α1=1. Значение α2 безразлично, так как даже при α1=α2=1 все равно α1 имеет более высокий приоритет. Если α1=0, а F3=1, то это значит, что требование прерывания вызвано запросом от ВУ2 (α2=1). При записи выражения (3.11) можно было руководствоваться следующими соображениями. F3=1 в двух случаях. Во-первых, если поступил запрос от ВУ1 (α1=1) и при этом МП-система ожидает запроса либо обслуживает прерывание от ВУ2 (в обоих случаях β2=0, см. таблицу 3.8). Во вторых, если поступил запрос от ВУ2 (α2=1) и при этом МП-сиcтема находится в состоянии ожидания (β1=β2=0). Сказанное соответствует двум составляющим выражения (3.11).
На втором примере мы прошли 2 этапа синтеза комбинационных цифровых электронных устройств:
1. Представление переключательных функций в форме, которая является исходной для выбранного метода минимизации - в нашем случае в виде таблицы истинности и диаграммы Вейча.
2. Получение минимальной ДНФ для каждого выхода комбинационной схемы.
3.12.2.2 Минимизация ПФ с помощью карт Карно
На рисунке 3.5 показан пример карты Карно для ПФ четырех переменных (n=4).
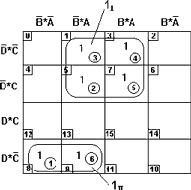
Рисунок 3.5
Каждая клетка в картах Карно так же, как и в диаграммах Вейча соответствует определенному набору переменных. Соседние клетки соответствуют наборам, отличающимся значением одной из переменных. Каждая строка и столбец обозначаются значением конкретной переменной или комбинацией (произведением) переменных в прямой или инверсной форме.
Клетки, помеченные переменными в прямой форме, соответствуют наборам, где эти переменные принимают единичные значения, а клетки, обозначенные переменными в инверсной форме – наборам, где эти переменные равны нулям.
Карты Карно удобно использовать, если ПФ задана в виде булевого выражения в СДНФ.
Например,
![]()
![]() (3.14)
(3.14)
Правила минимизации с помощью карт Карно в основном аналогичны правилам, изложенным при рассмотрении диаграмм Вейча. Отличие состоит в заполнении карты Карно единицами. Если диаграмма Вейча заполняется единицами в соответствии с номерами наборов, на которых исходная ПФ принимает единичное значение, то в карте Карно единицы ставят в клетки, лежащие на пересечении строк и столбцов карты, помеченных комбинациями переменных, которые при их перемножении дают запись соответствующей конституенты единицы (конъюнкции) в булевом выражении минимизируемой функции (3.14). На рисунке 3.5 показан пример заполнения карты Карно по выражению (3.14), содержащему шесть конституент единиц.
Булево выражение минимизированной ПФ имеет вид
![]() .(3.15)
.(3.15)
Другие примеры использования диаграмм Вейча и карт Карно показаны в [3, 18].
4. ЛОГИЧЕСКИЕ ЭЛЕМЕНТЫ
Для аппаратной реализации булевых выражений используется некоторый набор логических элементов, выпускаемых в виде интегральных микросхем (ИМС). Существуют специализированные ИМС, разработанные методами интегральной технологии специально для получения требуемой логической зависимости. Специализированные ИМС не требуют никаких паяных межсоединений и обладают высокой надежностью. Однако разработка подобных микросхем экономически оправдана лишь при большом объеме выпуска. Примером может служить массовый выпуск специализированных БИС для электронных часов, микрокалькуляторов и т.д.
Помимо специализированных ИМС имеется универсальный набор логических элементов в виде ИМС, обеспечивающий реализацию любых логических функций. К этому набору можно отнести: инвертор; конъюнктор; дизъюнктор; повторитель; И-НЕ; ИЛИ-НЕ; исключающее ИЛИ; сложение по модулю два (нечетность); сложение по модулю два с отрицанием (четность); эквивалентность; неэквивалентность; И-ИЛИ-НЕ; запрет и др.
Похожие работы
... правило, выполняется в виде одной «большой» ИМС. Схемотехника является частью микроэлектроники, предметом которой являются методы построения устройств различного назначения на микросхемах широкого применения. Предметом же цифровой схемотехники являются методы построения (проектирования) устройств только на цифровых ИМС. Особенностью цифровой схемотехники является широкое применение для описания ...
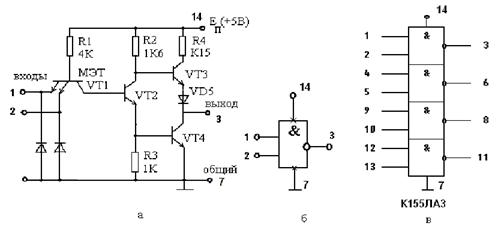
осхемы К155ЛА3 (4 логических элемента 2И-НЕ). Принцип работы ЛЭ И-НЕ ТТЛ Основная особенность микросхем ТТЛ состоит в том, что во входной цепи используется специфический интегральный прибор – многоэмиттерный транзистор (МЭТ), имеющий несколько эмиттеров, объединенных общей базой. Эмиттеры расположены так, что непосредственное взаимодействие между ними через участок базы отсутствует. Поэтому МЭТ ...
... . Минимальное количество листов графических работ формата А1 — два. Графические документы выполняются карандашом или черной тушью на листах ватмана формата А1. Возможно выполнение чертежей с применением ЭВМ. Допускается использовать формат А2. Листы нумеруются. Номер помещается в верхнем левом углу листа. Допускается выполнять номера на отдельных листах бумаги, которые прикрепляются во время ...
устройств вычислительной техники. Задачи проекта: Разработать печатную плату устройства управления питания компьютерной системы, произвести выбор и обоснование технологического процесса изготовления печатной платы, с исходными данными к проекту: схема электрическая принципиальная. Объём и содержание расчётно-пояснительной записки и графических работ произвести согласно техническому заданию. ...
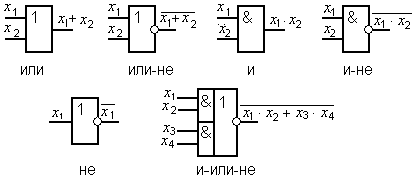


0 комментариев