Навигация
Отношения эквивалентности и толерантности и их свойства
МИНИСТЕРСТВО ОБРАЗОВАНИЯ РЕСПУБЛИКИ БЕЛАРУСЬ
"Гомельский государственный университет имени Франциска Скорины"
математический факультет
Кафедра алгебры и геометрии
Курсовая работа
"Отношения эквивалентности и толерантности и их свойства"
Гомель 2005
Введение
В обыденной речи мы часто говорим об одинаковости (о равенстве) каких-то объектов (предметов, множеств, абстрактных категорий), не заботясь о надлежащем уточнении смысла, который мы вкладываем в слово "одинаковый". В главе первой попробуем выявить и раскрыть понятие "одинаковости", определим термины "эквивалентность" и "отношение эквивалентности".
Не менее важной является ситуация, когда нам приходится устанавливать сходство объектов. Если одинаковость объектов означает их взаимозаменимость в некоторой ситуации, то сходство – это частичная взаимозаменимость, т.е. возможность взаимной замены с некоторыми (допустимыми в данной ситуации) потерями, с допустимым риском. Во второй главе попробуем раскрыть понятие "толерантности" на базе таких терминов, как "одинаковость" и "сходство" объектов.
А в третьей главе подробнее рассмотрим применение понятий отношений эквивалентности и толерантности в различных областях знаний и практики человека.
Реферат
![]()
Курсовая работа содержит: 41 страница, 3 источника, 1 приложение.
Ключевые слова: отношение эквивалентности, отношение толерантности, одинаковость, сходство, взаимозаменимость, классы эквивалентности, пространство толерантности, классы толерантности, предкласс, базис.
Объект исследования: отношения эквивалентности и толерантности.
Предмет исследования: свойства отношений эквивалентности и толерантности.
Цель работы: используя рекомендуемую литературу рассмотреть понятия отношений эквивалентности и толерантности; рассмотреть приложения этих понятий в различных областях знаний и практики человека.
Методы исследования: методы теории множеств и теории отношений.
Задачами курсовой работы являются: изучить свойства отношений эквивалентности и толерантности и их приложения в конкретных областях знаний.
1. Отношение эквивалентности
1.1 Определение и примеры
1.1.1 Определение
Систему непустых подмножеств ![]() множества
множества ![]() мы будем называть разбиением этого множества, если
мы будем называть разбиением этого множества, если
1) ![]() и
и
2) ![]() при
при ![]() .
.
Сами множества ![]() называются при этом классами данного разбиения.
называются при этом классами данного разбиения.
1.1.2 Определение
Отношение ![]() на множестве
на множестве ![]() называется эквивалентностью (или отношением эквивалентности), если существует разбиение
называется эквивалентностью (или отношением эквивалентности), если существует разбиение ![]() множества
множества ![]() такое, что соотношение
такое, что соотношение ![]() выполняется тогда и только тогда, когда
выполняется тогда и только тогда, когда ![]() и
и ![]() принадлежат некоторому общему классу
принадлежат некоторому общему классу ![]() данного разбиения.
данного разбиения.
Пусть ![]() – разбиение множества
– разбиение множества ![]() . Определим, исходя из этого разбиения, отношение
. Определим, исходя из этого разбиения, отношение ![]() на
на ![]() :
: ![]() , если
, если ![]() и
и ![]() принадлежат некоторому общему классу
принадлежат некоторому общему классу ![]() данного разбиения. Очевидно, отношение
данного разбиения. Очевидно, отношение ![]() является эквивалентностью. Назовем
является эквивалентностью. Назовем ![]() отношением эквивалентности, соответствующим исходному разбиению.
отношением эквивалентности, соответствующим исходному разбиению.
Например, разбиение состоит из подмножеств множества ![]() , содержащих ровно по одному элементу. Соответствующее отношение эквивалентности есть отношение равенства
, содержащих ровно по одному элементу. Соответствующее отношение эквивалентности есть отношение равенства ![]() . Наконец, если разбиение множества
. Наконец, если разбиение множества ![]() состоит из одного подмножества, совпадающего с самим
состоит из одного подмножества, совпадающего с самим ![]() , то соответствующее отношение эквивалентности есть полное отношение: любые два элемента являются эквивалентными.
, то соответствующее отношение эквивалентности есть полное отношение: любые два элемента являются эквивалентными.
Пустое отношение (на непустом множестве!) не является эквивалентностью.
Мы подошли к эквивалентности через понятие взаимозаменимости. Но что значит, что два объекта ![]() и
и ![]() взанмозамепимы в данной ситуации? Это всегда можно понимать так, что каждый из них содержит всю информацию о другом объекте, небезразличную в данной ситуации. Это утверждение означает только то, что взаимозаменимость объектов есть совпадение признаков, существенных в данной ситуации.
взанмозамепимы в данной ситуации? Это всегда можно понимать так, что каждый из них содержит всю информацию о другом объекте, небезразличную в данной ситуации. Это утверждение означает только то, что взаимозаменимость объектов есть совпадение признаков, существенных в данной ситуации.
Например, пусть мы считаем одинаковыми автомобили, выпущенные в одной и той же серии одним и тем же заводом. Тогда, разобрав один экземпляр "Волги", мы в принципе можем составить комплект рабочих чертежей, который годится для выпуска однотипных "Волг". Однако, изучив один экземпляр "Волги", мы не можем угадать окраску кузова или характер вмятин на бампере у других односерийных экземпляров.
Когда мы выбираем из комплекта одну шахматную фигуру, то мы знаем, куда ее можно поставить в начальной позиции и как ходят, все взаимозаменяемые с ней, т.е. одноименные и одноцветные, фигуры.
Пусть теперь задано разбиение ![]() множества
множества ![]() . Выберем в каждом множестве
. Выберем в каждом множестве ![]() некоторый содержащийся в нем элемент
некоторый содержащийся в нем элемент ![]() . Этот элемент мы будем называть эталоном для всякого элемента
. Этот элемент мы будем называть эталоном для всякого элемента ![]() , входящего в то же множество
, входящего в то же множество ![]() . Мы будем – по определению – полагать выполненным соотношение
. Мы будем – по определению – полагать выполненным соотношение ![]() . Так определенное отношение
. Так определенное отношение ![]() назовем отношением "быть эталоном".
назовем отношением "быть эталоном".
Легко видеть, что эквивалентность ![]() , соответствующая исходному разбиению, может быть определена так:
, соответствующая исходному разбиению, может быть определена так: ![]() , если
, если ![]() и
и ![]() имеют общий эталон:
имеют общий эталон: ![]() и
и ![]() .
.
Ясно, что любое отношение эквивалентности может быть таким образом определено с помощью отношения "быть эталоном" и, наоборот, любое отношение "быть эталоном" определяет некоторую эквивалентность.
Пусть ![]() – отношение эквивалентности, а
– отношение эквивалентности, а ![]() – такое отношение "быть эталоном", что
– такое отношение "быть эталоном", что ![]() выполнено в том и только том случае, когда
выполнено в том и только том случае, когда ![]() и
и ![]() имеют общий эталон
имеют общий эталон ![]() .
.
Иначе говоря, ![]() равносильно существованию такого
равносильно существованию такого ![]() , что
, что ![]() и
и ![]() . Поскольку
. Поскольку ![]() , это означает, что
, это означает, что ![]() . Иначе говоря, эквивалентность можно алгебраически выразить через более простое отношение "быть эталоном". Отношение
. Иначе говоря, эквивалентность можно алгебраически выразить через более простое отношение "быть эталоном". Отношение ![]() на множестве из
на множестве из ![]() элементов можно задать графом, имеющим ровно
элементов можно задать графом, имеющим ровно ![]() стрелок, где
стрелок, где ![]() – число классов эквивалентности: каждый элемент соединяется со своим единственным эталоном. Граф, изображающий отношение эквивалентности, состоит из
– число классов эквивалентности: каждый элемент соединяется со своим единственным эталоном. Граф, изображающий отношение эквивалентности, состоит из ![]() полных подграфов, содержащих по
полных подграфов, содержащих по ![]() , вершин
, вершин ![]() . Таким образом, общее число ребер в этом графе равно
. Таким образом, общее число ребер в этом графе равно ![]() .
.
Рассмотрим в качестве ![]() множество всех целых неотрицательных чисел и возьмем его разбиение на множество
множество всех целых неотрицательных чисел и возьмем его разбиение на множество ![]() четных чисел и множество
четных чисел и множество ![]() нечетных чисел. Соответствующее отношение эквивалентности на множестве целых чисел обозначается так:
нечетных чисел. Соответствующее отношение эквивалентности на множестве целых чисел обозначается так: ![]() и читается:
и читается: ![]() сравнимо с
сравнимо с ![]() по модулю 2. В качестве эталонов здесь естественно выбрать 0 – для четных чисел и 1 – для нечетных чисел. Аналогично, разбивая то же множество
по модулю 2. В качестве эталонов здесь естественно выбрать 0 – для четных чисел и 1 – для нечетных чисел. Аналогично, разбивая то же множество ![]() на
на ![]() подмножеств
подмножеств ![]() , где
, где ![]() состоит из всех чисел, дающих при делении на
состоит из всех чисел, дающих при делении на ![]() и остатке
и остатке ![]() , мы придем к отношению эквивалентности:
, мы придем к отношению эквивалентности: ![]() , которое выполняется, если
, которое выполняется, если ![]() и
и ![]() имеют одинаковый остаток при делении на
имеют одинаковый остаток при делении на ![]() . В качестве эталона в каждом
. В качестве эталона в каждом ![]() естественно выбрать соответствующий остаток
естественно выбрать соответствующий остаток ![]() .
.
Похожие работы
... чем «я», делает мировосприятие более многомерным, целостным, а значит более адекватным реальности [10, c.23-27]. Глава 2. Государственно-правовое регулирование проблем толерантности в современном обществе 2.1 Анализ правовых актов по проблемам толерантности В Декларации о ликвидации всех форм дискриминации на основе религии или убеждений, которая была принята Генеральной Ассамблеей ООН 25 ...
... сигналов, передающихся от одного живого организма другому (от родителей - потомкам) или от одних клеток, тканей, органов другим в процессе развития особи; 6. в математике, кибернетике – количественная мера устранения энтропии (неопределенности), мера организации системы; 7. в философии – свойство материальных объектов и процессов сохранять и порождать определенное состояние, которое в ...
... в отечественной теории и практике психологических измерений. Хотя концепт осмысленности измерения развивается с трансформацией идей Стивенса и разработкой проблем статистики и логики, его положения относительно шкалирования, по проблемам измерений в психологии и связанной с ними осмысленностью измерений требуют, на наш взгляд, критического анализа привычной практики использования психологического ...
... N(X)N, состоящее из тех и только из тех i, для которых = 1. Это объясняет, почему изложение вероятностных и статистических результатов, относящихся к анализу данных, являющихся объектами нечисловой природы перечисленных выше видов, велось [37, гл.4] на языке конечных случайных множеств. Множества как исходные данные появляются и в иных постановках. Из геологических реалий исходил Ж.Матерон ...


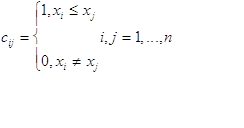
0 комментариев