Формальные свойства эквивалентности
Теорема
Теорема
Теорема
Лемма
Лемма
Отношения эквивалентности на числовой прямой
Пример
Операции над толерантностями
Определение
Лемма
Лемма
Лемма
Определение
Определение
Дальнейшее исследование структуры толерантностей
Теорема
Теорема
Та же ситуация для зацепленных циклических графов (см. рис. 6)
Приложение понятий эквивалентности и толерантности в различных областях знаний и практики человека
Навигация
Теорема
Отношения эквивалентности и толерантности и их свойства
66989
знаков
0
таблиц
0
изображений
1.2.2 Теорема
Если 
– конечное множество и 
– отношение эквивалентности на нем, то существуют такие 
и 
, что каждому элементу 
можно сопоставить кортеж (упорядоченный набор) из 
двоичных признаков (нулей или единиц):
, 
и т.д., так что 1) разным элементам соответствуют разные кортежи признаков и 2) для того, чтобы было 
, необходимо и достаточно, чтобы первые признаков этих элементов совпадали: 
.
Доказательство. Возьмем разбиение 
множества , соответствующее отношению . В силу конечности множества 
это разбиение конечно и каждый класс конечен. Перенумеруем элементы каждого класса. Тогда каждому элементу 
можно сопоставить пару целых чисел: 
, где 
– номер класса 
, в который попал , a 
– номер элемента в своем классе. Ясно, что если 
, 
и 
, то 
. Действительно, либо элементы и 
попали в разные классы – тогда у них различные первые номера; 
; либо они различаются номером в классе – тогда 
. Представим теперь числа и в двоичной системе счисления. Пусть – наибольшее число разрядов у чисел , а – наибольшее число разрядов у чисел . Если некоторое имеет меньше, чем разрядов, то дополним его слева нулями. Так же поступим и со вторыми номерами. Тем самым каждому элементу будет сопоставлен кортеж из двоичных признаков.
Для завершении доказательства достаточно заметить, что эквивалентность элементов и означает попадание в общий класс, т.е. совпадение первых номеров (первых признаков).
Эта теорема оправдывает сделанное ранее утверждение, что любая эквивалентность на конечном множестве, может быть задана как совпадение некоторого, набора общих признаков.
Итак, оба наши определения эквивалентности равносильны. Но теперь возникает вопрос, не являются ли некоторые аксиомы эквивалентности излишними. Например, быть может, из рефлексивности и симметричности уже следует транзитивность отношения?
Вернемся к обсуждению отношения : " является эталоном для ". Мы уже дали конструктивное определение этого отношения. Из него легко можно получить следующие свойства отношения (быть эталоном):
1) для всякого существует эталон : .
2) Если , то 
, т.е. любой эталон есть эталон для самого себя.
3) Эталон единствен, т.е. из и 
следует 
.
Эти три свойства можно объявить аксиомами отношения "быть эталоном". Покажем, что из них следует определение эталона с помощью разбиения. Для этого сначала по отношению построим новое отношение 
, определяемое правилом: 
, если и имеют общий эталон. Иначе говоря, если существует такое 
, что 
и . Покажем, что есть отношение эквивалентности. Действительно, по свойству 1) у каждого есть эталон и, стало быть, 
. Значит, рефлексивно. Симметричность отношения очевидна. Если и 
, то это значит, что и имеют общий эталон, а не может иметь эталона, отличного от эталона для . Значит, 
.
Итак, доказано, что есть отношение эквивалентности. Но тогда по теореме 1.2.1 существует разбиение множества на классы эквивалентных друг другу элементов – так называемые классы эквивалентности.
Очевидно, каждый класс эквивалентности 
состоит из всех элементов, имеющих общий эталон 
. По свойству 2) 
и, значит, 
. Таким образом, отношение , определенное аксиоматически свойствами 1) – 3), всегда может быть задано разбиением с выбранными представителями (эталонами) в каждом классе.
Пусть 
– сюръективное отображение множества на некоторое множество 
. Рассмотрим на множестве отношение "иметь общий образ" и обозначим это отношение 
. Иначе говоря, 
, если 
. Обозначим через 
множество всех элементов , имеющих данный образ 
, т.е. таких, что 
. Ясно, что 
, так как любой элемент из имеет образ. Далее, при разных 
и 
, 
, так как иначе элемент, попавший в пересечение 
, имел бы два разных образа: и . Поскольку 
сюръективно, 
для любого . Итак, множества образуют разбиение множества , а отношение есть эквивалентность, соответствующая этому разбиению. Последнее следует из того, что тогда и только тогда, когда и принадлежат общему, множеству .
Множество классов эквивалентности по отношению принято обозначать 
(читается: фактормножество множества по отношению ). Наши рассуждения показывают, что для всякого сюръективного отображения существует отношение эквивалентности на множестве такое, что и могут быть поставлены во взаимно-однозначное соответствие.
Наоборот, если имеется произвольное отношение эквивалентности на , то по нему можно построить отображение , где 
и 
есть класс эквивалентности, содержащий . Легко проверить, что сюръективно и построенное по этому отображению отношение эквивалентности есть исходное отношение .
Рассмотрим частный случай, когда и 
. Пусть, далее, отображение обладает тем свойством, что, при 
, 
или, как говорят в таких случаях, подмножество неподвижно при отображении . Отсюда видно, что сюръективно. Действительно, всякий есть образ по крайней мере самого : 
. Итак, каждому 
однозначно сопоставлен некоторый элемент . При этом, если сопоставлен какому-то элементу, то самому сопоставлен он же.
Сравнивая с соответствующими свойствами, определяющими соотношение "быть эталоном", мы видим, что отображение множества на неподвижное подмножество задает на отношение "быть эталоном" так, что в том и только том случае, когда 
.
Посмотрим теперь, что получится, если отказаться от условии, что определено на всем . Рассмотрим функцию , которая некоторым элементам из сопоставляет единственный образ из . По отображению можно опять-таки построить отношение по правилу: , если . Легко проверить, что будет симметрично и транзитивно. Выберем подмножество 
, состоящее из тех элементов, на которых определено отображение . Тогда если либо , либо не принадлежат 
, то заведомо не выполняется. Значит, если не входит в , то 
также не выполнено. Следовательно, отношение теперь уже не обязано быть рефлексивным.
Видно, как построить пример симметричного и транзитивного, но не рефлексивного отношения. Пусть – множество людей, а отношение означает "быть уроженцем одного города". Легко видеть, что симметрично и транзитивно, но если родился не в городе, а в деревне, или, вообще, во время путешествия по морю, то не выполнено. В этом примере – множество городов, а отображение сопоставляет каждому человеку город, где он был рожден.
Из сказанного видно также, что условие рефлексивности можно в определении эквивалентности заменить более слабым. Достаточно потребовать, чтобы для каждого существовал такой элемент , что выполнено либо , либо 
. Тогда из этого свойства, а также симметричности и транзитивности можно получить рефлексивность отношения .
Граф, изображающий отношение эквивалентности, выглядит следующим образом. Пусть – множество его вершин. Тогда 
, где – классы эквивалентности. Ясно, что в каждом подмножестве все вершины соединены друг с другом. Но никакая из них не соединена с вершинами, не входящими в . Итак, граф, изображающий отношение эквивалентности, состоит из отдельных, не связанных друг с другом полных подграфов.
Прямой суммой отношений 
и 
называется отношение 
. Прямую сумму отношений , мы будем обозначать через 
.
Таким образом, соотношение выполнено в следующих случаях: 1) 
, 
и 
; 2) 
, 
и 
;
Похожие работы
... чем «я», делает мировосприятие более многомерным, целостным, а значит более адекватным реальности [10, c.23-27]. Глава 2. Государственно-правовое регулирование проблем толерантности в современном обществе 2.1 Анализ правовых актов по проблемам толерантности В Декларации о ликвидации всех форм дискриминации на основе религии или убеждений, которая была принята Генеральной Ассамблеей ООН 25 ...
... сигналов, передающихся от одного живого организма другому (от родителей - потомкам) или от одних клеток, тканей, органов другим в процессе развития особи; 6. в математике, кибернетике – количественная мера устранения энтропии (неопределенности), мера организации системы; 7. в философии – свойство материальных объектов и процессов сохранять и порождать определенное состояние, которое в ...
... в отечественной теории и практике психологических измерений. Хотя концепт осмысленности измерения развивается с трансформацией идей Стивенса и разработкой проблем статистики и логики, его положения относительно шкалирования, по проблемам измерений в психологии и связанной с ними осмысленностью измерений требуют, на наш взгляд, критического анализа привычной практики использования психологического ...
... N(X)N, состоящее из тех и только из тех i, для которых = 1. Это объясняет, почему изложение вероятностных и статистических результатов, относящихся к анализу данных, являющихся объектами нечисловой природы перечисленных выше видов, велось [37, гл.4] на языке конечных случайных множеств. Множества как исходные данные появляются и в иных постановках. Из геологических реалий исходил Ж.Матерон ...
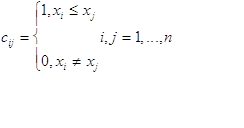
0 комментариев