Формальные свойства эквивалентности
Теорема
Теорема
Теорема
Лемма
Лемма
Отношения эквивалентности на числовой прямой
Пример
Операции над толерантностями
Определение
Лемма
Лемма
Лемма
Определение
Определение
Дальнейшее исследование структуры толерантностей
Теорема
Теорема
Та же ситуация для зацепленных циклических графов (см. рис. 6)
Приложение понятий эквивалентности и толерантности в различных областях знаний и практики человека
Навигация
Теорема
Отношения эквивалентности и толерантности и их свойства
66989
знаков
0
таблиц
0
изображений
1.2.3 Теорема
Если 
, а отношения 
и 
– эквивалентности, то их прямая сумма 
также является эквивалентностью.
Доказательство. Рефлексивность проверяется просто: если 
, то выполнено 
и, следовательно, 
. Симметричность также очевидна: если выполнено 
, то либо 
и 
входят в 
и 
, а значит, и 
, т.е. 
, либо и входят в 
и 
, поэтому 
и . Докажем транзитивность отношения 
. Пусть выполнены соотношения и 
. Рассмотрим случай, когда 
и . Так как , то не входит в . Но тогда соотношение может выполняться только при 
и 
. Однако, из и вытекает 
и 
. Случай, когда и принадлежат , исследуется аналогично. Теорема доказана.
Замечание. Из этого доказательства видно, что условие непустоты пересечения работало только при проверке транзитивности. Значит, справедлива.
1.2.4 Теорема
Если отношения 
и 
рефлексивны и симметричны (в частности, являются эквивалснтиостями), то их прямая сумма 
также рефлексивна и симметрична.
Замечание. Если 
, то каждое из отношений и есть сужение отношения 
на свою область задания.
1.3 Операции над эквивалентностями
Посмотрим, какие операции над отношениями эквивалентности и при каких условиях дают в результате эквивалентность.
Транзитивное замыкание 
отношения эквивалентности является отношением эквивалентности.
Отношение, обратное к эквивалентности, является эквивалентностью.
Если и 
– эквивалентности, то их пересечение 
также является отношением эквивалентности.
Сложнее обстоит дело с объединением отношений эквивалентности. Вообще говоря, объединение эквивалентностей уже не обязано быть эквивалентностью.
Действительно, отношение дает разбиение на два класса 
и 
, отношению соответствует разбиение 
, а отношение дает неполный связный граф.
Теперь попробуем разобраться, когда объединение эквивалентностей дает в результате эквивалентность. Пусть 
, тогда из свойств теоретикомножественных операций следует 
, т.е. 
есть эквивалентность. Точно так же, если 
, то является эквивалентностью.
Рассмотрим более общий случай, когда множество 
можно разбить на два непересекающихся подмножества и (из которых одно может быть пустым) так что
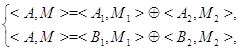(1)
и при этом
(2)
В этом случае отношения и мы назовем когерентными.
Легко видеть, что если или , то отношения и когерентны (надо положить 
, 
). Таким образом, сравнимость относительно "порядка", задаваемого включением, есть частный случай когерентности.
Из (2) следует, что для когерентных отношении эквивалентности и : 
и 
. Используя определение прямой суммы и (23), получаем 
. Здесь 
и – эквивалентности (как сужения эквивалентиостей 
и ), а , и не пересекаются. По теореме 1.2.3 отсюда следует, что есть отношение эквивалентности.
Оказывается, когерентность отношений , является не только достаточным, но и необходимым условием для того, чтобы объединение эквивалентностей и было эквивалентностью.
Похожие работы
... чем «я», делает мировосприятие более многомерным, целостным, а значит более адекватным реальности [10, c.23-27]. Глава 2. Государственно-правовое регулирование проблем толерантности в современном обществе 2.1 Анализ правовых актов по проблемам толерантности В Декларации о ликвидации всех форм дискриминации на основе религии или убеждений, которая была принята Генеральной Ассамблеей ООН 25 ...
... сигналов, передающихся от одного живого организма другому (от родителей - потомкам) или от одних клеток, тканей, органов другим в процессе развития особи; 6. в математике, кибернетике – количественная мера устранения энтропии (неопределенности), мера организации системы; 7. в философии – свойство материальных объектов и процессов сохранять и порождать определенное состояние, которое в ...
... в отечественной теории и практике психологических измерений. Хотя концепт осмысленности измерения развивается с трансформацией идей Стивенса и разработкой проблем статистики и логики, его положения относительно шкалирования, по проблемам измерений в психологии и связанной с ними осмысленностью измерений требуют, на наш взгляд, критического анализа привычной практики использования психологического ...
... N(X)N, состоящее из тех и только из тех i, для которых = 1. Это объясняет, почему изложение вероятностных и статистических результатов, относящихся к анализу данных, являющихся объектами нечисловой природы перечисленных выше видов, велось [37, гл.4] на языке конечных случайных множеств. Множества как исходные данные появляются и в иных постановках. Из геологических реалий исходил Ж.Матерон ...
0 комментариев