Навигация
Дальнейшее исследование структуры толерантностей
2.6 Дальнейшее исследование структуры толерантностей
Рассмотрим множество ![]() и его покрытие
и его покрытие ![]() . Пару
. Пару ![]() мы будем далее называть картой.
мы будем далее называть картой.
Произвольная карта ![]() позволяет ввести на множестве
позволяет ввести на множестве ![]() отношение толерантности
отношение толерантности ![]() , определенное условием:
, определенное условием: ![]() , если существует такое
, если существует такое ![]() , что одновременно
, что одновременно ![]() и
и ![]() . Так определенную толерантность
. Так определенную толерантность ![]() мы назовем толерантностью, порожденную картон
мы назовем толерантностью, порожденную картон ![]() . Очевидно, каждое
. Очевидно, каждое ![]() является предклассом порожденной толерантности
является предклассом порожденной толерантности ![]() .
.
Если ![]() – пространство толерантности и
– пространство толерантности и ![]() – множество всех классов толерантности в этом пространстве, то, в силу леммы 2.3.3 толерантность, порожденная картой
– множество всех классов толерантности в этом пространстве, то, в силу леммы 2.3.3 толерантность, порожденная картой ![]() , совпадает с исходной толерантностью
, совпадает с исходной толерантностью ![]() . Аналогичное утверждение справедливо и для произвольного базиса
. Аналогичное утверждение справедливо и для произвольного базиса ![]() в пространстве
в пространстве ![]() .
.
Карта ![]() называется канонической, если каждый элемент
называется канонической, если каждый элемент ![]() покрытия
покрытия ![]() оказывается классом толерантности, порожденной исходной картон
оказывается классом толерантности, порожденной исходной картон ![]() . Легко видеть, что если карта
. Легко видеть, что если карта ![]() является канонической, то
является канонической, то ![]() содержит некоторый базис
содержит некоторый базис ![]() , порожденный толерантности:
, порожденный толерантности: ![]() .
.
На рис. 1 изображена некоторая карта ![]() , а справа система классов порожденной толерантности (впрочем, в данном случае эта система состоит из одного класса). Этот пример показывает, в частности, существование неканонических карт.
, а справа система классов порожденной толерантности (впрочем, в данном случае эта система состоит из одного класса). Этот пример показывает, в частности, существование неканонических карт.
Каждая карта ![]() естественным образом приводит к всюду определенному соответствию
естественным образом приводит к всюду определенному соответствию
![]() (25)
(25)
которое каждому элементу ![]() сопоставляет все те
сопоставляет все те ![]() , для которых
, для которых ![]() . Наоборот, если дано некоторое всюду определенное соответствие
. Наоборот, если дано некоторое всюду определенное соответствие ![]() , то оно порождает покрытие
, то оно порождает покрытие ![]() множества
множества ![]() , состоящее из прообразов элементов из
, состоящее из прообразов элементов из ![]() при соответствии
при соответствии ![]() . Таким образом,
. Таким образом, ![]() тогда и только тогда, когда существует такое
тогда и только тогда, когда существует такое ![]() , что
, что ![]() есть множество элементов из
есть множество элементов из ![]() , которым соответствие
, которым соответствие ![]() сопоставляет
сопоставляет ![]() . Обозначим для дальнейшего прообраз элемента
. Обозначим для дальнейшего прообраз элемента ![]() при соответствии
при соответствии ![]() через
через ![]() .
.
По соответствию (25) можно построить отображение,
![]() (26)
(26)
которое каждому элементу ![]() сопоставляет непустое множество элементов
сопоставляет непустое множество элементов ![]() , для которых
, для которых ![]() . С помощью отображении (26) толерантность
. С помощью отображении (26) толерантность ![]() , порожденная исходной картой
, порожденная исходной картой ![]() , выражается условием
, выражается условием ![]() , если
, если ![]() . Можно ввести еще и отношение
. Можно ввести еще и отношение ![]() , определяемое условием:
, определяемое условием: ![]() , если
, если ![]() .
. ![]() , очевидно, является эквивалентностью.
, очевидно, является эквивалентностью.
Посмотрим на примерах, как канонические признаки выражаются через исходные признаки карты. В примере на рис. 1 Имеем ![]() .
.
В примере на рис. 2а, изображено соответствие: ![]() , где
, где ![]() ,
, ![]() . Нa рис. 2б изображены классы порожденной толерантности. Легко проверить, что
. Нa рис. 2б изображены классы порожденной толерантности. Легко проверить, что ![]() ,
, ![]() .
.
На рис 3 исходная карта уже является канонической. Но если взять каноническую карту ![]() с полным набором классов толерантности, то получим, что
с полным набором классов толерантности, то получим, что ![]() . Посмотрим далее, каким образом и всегда ли канонические признаки могут быть выражены через исходные.
. Посмотрим далее, каким образом и всегда ли канонические признаки могут быть выражены через исходные.
Похожие работы
... чем «я», делает мировосприятие более многомерным, целостным, а значит более адекватным реальности [10, c.23-27]. Глава 2. Государственно-правовое регулирование проблем толерантности в современном обществе 2.1 Анализ правовых актов по проблемам толерантности В Декларации о ликвидации всех форм дискриминации на основе религии или убеждений, которая была принята Генеральной Ассамблеей ООН 25 ...
... сигналов, передающихся от одного живого организма другому (от родителей - потомкам) или от одних клеток, тканей, органов другим в процессе развития особи; 6. в математике, кибернетике – количественная мера устранения энтропии (неопределенности), мера организации системы; 7. в философии – свойство материальных объектов и процессов сохранять и порождать определенное состояние, которое в ...
... в отечественной теории и практике психологических измерений. Хотя концепт осмысленности измерения развивается с трансформацией идей Стивенса и разработкой проблем статистики и логики, его положения относительно шкалирования, по проблемам измерений в психологии и связанной с ними осмысленностью измерений требуют, на наш взгляд, критического анализа привычной практики использования психологического ...
... N(X)N, состоящее из тех и только из тех i, для которых = 1. Это объясняет, почему изложение вероятностных и статистических результатов, относящихся к анализу данных, являющихся объектами нечисловой природы перечисленных выше видов, велось [37, гл.4] на языке конечных случайных множеств. Множества как исходные данные появляются и в иных постановках. Из геологических реалий исходил Ж.Матерон ...


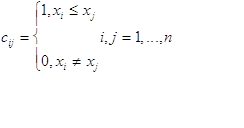
0 комментариев