Навигация
Ние системы
0 ние системы.
Для линейных систем большинство оценок можно получить без прямого
интегрирования дифференциальных уравнений САР. При действии на САР
- 55 -
случайных возмущений распространенным критерием качества динамической
точности служит средняя квадратическая погрешность, являющаяся харак-
теристикой рассеивания возможных значений случайной величины относи-
тельно их среднего значения и определяемая как положительное значение
квадратного корня из дисперсии случайной величины.
Наряду с этими оценками при синтезе систем со случайными воздейс-
твиями используют удельный риск, общий риск и другие критерии качест-
ва.
Частотные характеристики.
Если передаточную функцию стационарной системы записать в виде
p=jw (43), то функция вида
W(jw)=(B 4o 0(jw) 5m 0+B 41 0(jw) 5m-1 0+...+B 4m 0)/(A 4o 0(jw) 5n 0+A 41 0(jw) 5n-1 0+...+A 4n 0) (44) будет
частотной передаточной функцией. Ее можно представить в виде
W(jw)=U(w)+jV(w)=A(w)e 5jF(w) 0 (45), A(w)= 7? 0(U 52 0(w)+V 52 0(w)) (46),
F(w)=argW(jw) (47). На комплексной плоскости частотная передаточная
функция определяет вектор ОС, длина (модуль ) которого равна A(w), а
угол, образованный этим вектором с действительной положительной полу-
осью, равен F(w). Кривая, которую описывает конец этого вектора при
изменении частоты от нуля до бесконечности, называется амплитудно-фа-
зо-частотной характеристикой (АФЧХ).
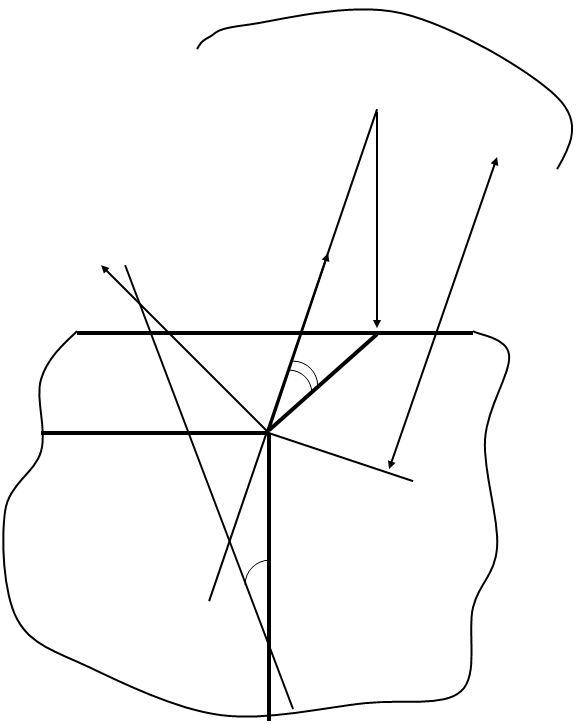
──────────────────────────────────────────────────────────────────────
│jV
│
│ U(w)
─────────────┼───────┬─────────
0│\ F(w) │ U
│ \ │
│ \ │
V(w)├──────\C
│
Рис. 11. АФЧХ
──────────────────────────────────────────────────────────────────────
Действительную часть U(w)=ReW(jw) (48) и мнимую часть
V(w)=ImW(jw) (49) называют соответственно вещественной и мнимой час-
тотными функциями. График вещественной частотной характеристики (кри-
вая U=U(w) при изменении w от 0 до бесконечности) называют веществен-
ной частотной характеристикой, а график мнимой частотной функции -
мнимой частотной характеристикой. Модуль A(w)=│W(j)│ - амплитудная
частотная функция, а ее график - амплитудная частотная характеристика.
Аргумент F(w)=argW(jw) называют фазовой частотной функцией, а ее гра-
фик - фазовой частотной характеристикой. Установим, какой физический
смысл имеют частотные характеристики. Если на вход устойчивой линейной
стационарной системы подается гармонический сигнал u=a*sin(wt), то на
ее выходе после окончания переходного процесса устанавливается гармо-
нический процесс с амплитудой в и фазой, сдвинутой относительно фазы
входного сигнала на угол f. Амплитуда в и сдвиг фазы f зависят от час-
тоты входного сигнала и свойства системы. Кроме того, амплитуда в за-
висит еще от амплитуды входного сигнала. Но отношение в/а не зависит
от амплитуды а. Оказывается, что в/а=A(w) и F=F(w), т.е. амплитудная
частотная характеристика равна отношению амплитуды выходного сигнала к
амплитуде входного гармонического сигнала (в установившемся режиме), а
фазовая частотная функция - сдвигу фазы выходного сигнала.
Временные характеристики.
Переходные и импульсные переходные характеристики называются вре-
менными. Они используются при описании линейных систем как стационар-
ных, так и нестационарных. Переходной функцией звена называется функ-
ция h(t), которая описывает его реакцию (изменение выходной величины)
- 56 -
на единичное ступенчатое воздействие 1(t) при нулевых начальных усло-
виях.
По определению, 1(t)= 7( 01, t>0
79 00, t<0 (50).
График переходной функции - кривая зависимости h(t) от времени t
называется переходной или разгонной характеристикой.
Импульсной переходной или весовой функцией называется функция
w(t), которая описывает реакцию системы на единичное импульсное воз-
действие при нулевых начальных условиях. График импульсной переходной
функции называется импульсной переходной характеристикой. При опреде-
лении весовой функции использовано понятие единичного импульса. Еди-
ничный импульс - импульс с единичной площадью бесконечно малой дли-
тельности. Он описывается дельта-функцией, которая является одной из
обобщенных функций.
Устойчивость является одним из основных требований, предъявляемых
к системам автоматического регулирования. Неустойчивые системы нерабо-
тоспособны. Поэтому важно уметь определять и обеспечивать устойчивость
системы регулирования. Существуют различные понятия устойчивости.
Рассмотрим определение устойчивости по Ляпунову. Пусть САР описывается
дифференциальным уравнением в нормальной форме y' 4i 0=Y 4i 0(y 41 0,...,y 4n 0,t)
(51), i=1...n или в векторной форме y'=Y(y,t) (52), где y=(y 41 0,...,y 4n 0) 5т
и Y=(Y 41 5т 0,...Y 4n 5т 0) - вектор-столбцы (индекс "т" обозначает операцию
транспонирования).
Обозначим y 5o 0(t) невозмущенное движение. Оно является решением
уравнения (52) при определенных начальных условиях. Решение уравнения
(52) при любых других начальных условиях называется возмущенным движе-
нием. Представим уравнение (52) в отклонениях xi=yi-y 5o 0i (i=1,..n),
x'=X(x,t) (53) в уравнении x=(x 41 0,...,x 4n 0) 5т 0, X=(X 41 0,...,X 4n 0) 5т 0,
X 4i 0(x,t)=Y 4i 0(x+y 5о 0,t)+y' 5о 4i 0 (54), i=1,...,n. В новых переменных невозму-
щенным движением является решение x(t)=0 уравнения (53) при нулевых
начальных условиях. Любое другое решение x[x(t 4o 0),t], т.е. решение (53)
при произвольном начальном значении x(t 4o 0) 7- 00, определяет возмущенное
движение. Оно называется возмущением или начальным возмущением.
Переменные x 4i 0(y 4i 0), i=1,...,n называются фазовыми координатами, а
x(y) - фазовым вектором. Пространство n-мерных векторов x(y) называет-
ся фазовым пространством.
Невозмущенное движение x(t)=0 называется устойчивым по Ляпунову,
если, каково бы ни было e>0 , найдется такое b=b(e,t 4o 0)>0, что при лю-
бых t>t 4o 0 ││x[x(t 4o 0,t]││<e, как только ││x(t 4o 0)││<b. Здесь ││x││ -длина
вектора (евклидова норма):
4n
││x││= 7S 0(x 52 4i 0) 51/2
51
Похожие работы
... гарантійного ремонту). В конструкції кришки для цього передбачено пломбувальний "стакан", що під час складання виробу на виробництві заповнюється пломбувальною пастою перед загвинчуванням гвинта. 2.2 Технологічний аналіз елементної бази В своєму складі блок живлення БП-9/4 має таку елементну базу: мікросхема, транзистор, діоди, конденсатори, резистори постійні та змінні. Усі перелічені ЕРЕ ...
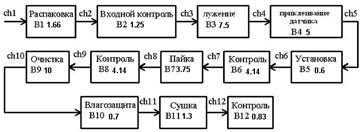
... выполнения норм времени, принимаем равным 1. Результаты расчета показателей поточной линии сборки приведены в таблице 1.2. Маршрутное описание технологического процесса производства модуля сопряжения цифрового мультиметра с компьютером представлено в приложении в виде маршрутных карт. Таблица 1.2 – Результаты расчета показателей поточной линии сборки Операция Оборудование Производит
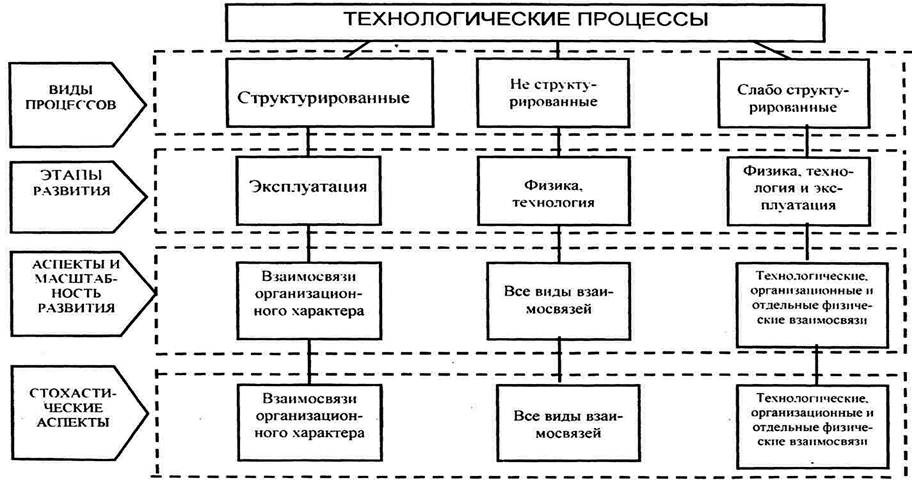
... 0mil 0.0deg (0.0mil,0.0mil) Flash"* Выполнив сверление отверстий в ПП, робот выполняет установку ЭРЭ. После установки ЭРЭ, плату отправляют на пайку волной припоя. 2 МОДЕЛИРОВАНИЕ ТЕХНОЛОГИЧЕСКОГО ПРОЦЕССА Моделирование – это метод исследования сложных систем, основанный на том, что рассматриваемая система заменяется на модель и проводится исследование модели с целью получения информации об ...
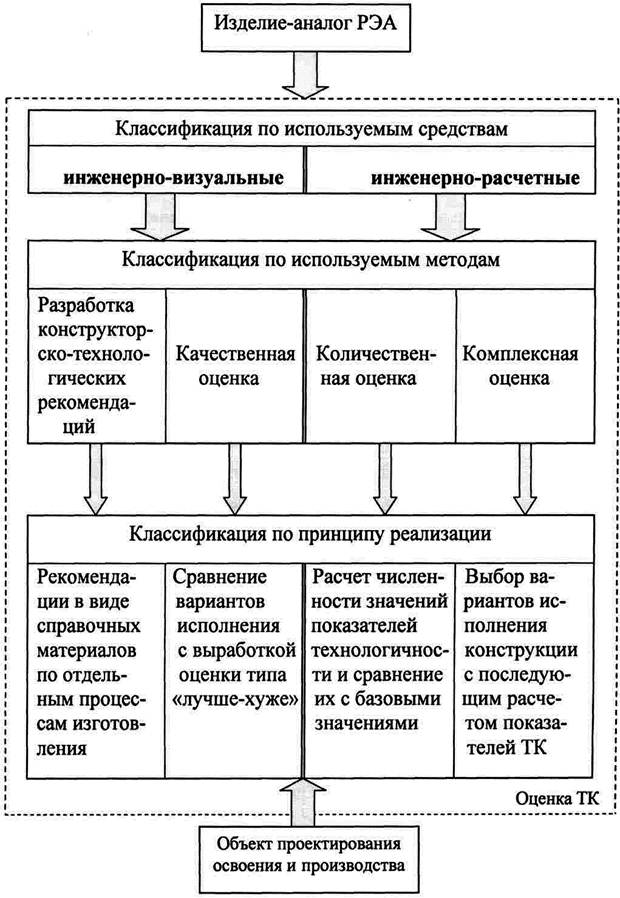
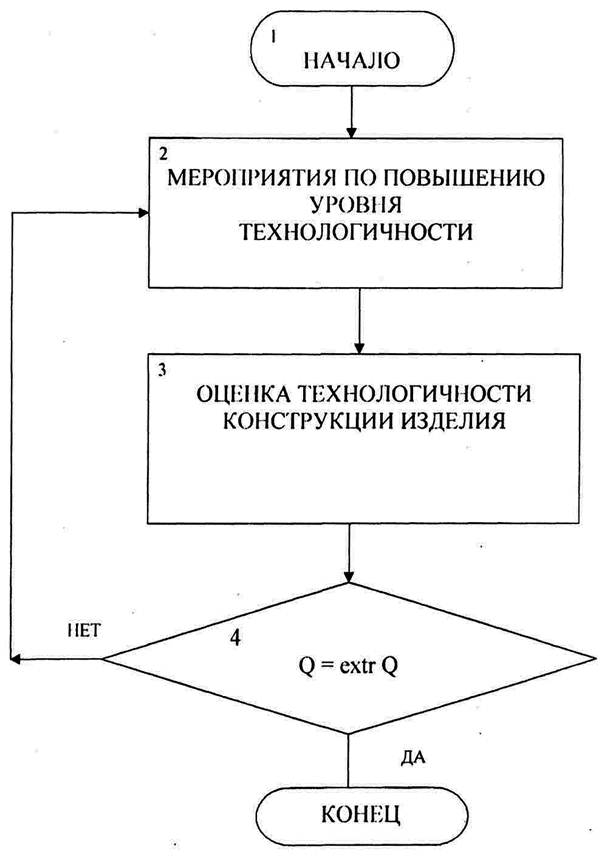
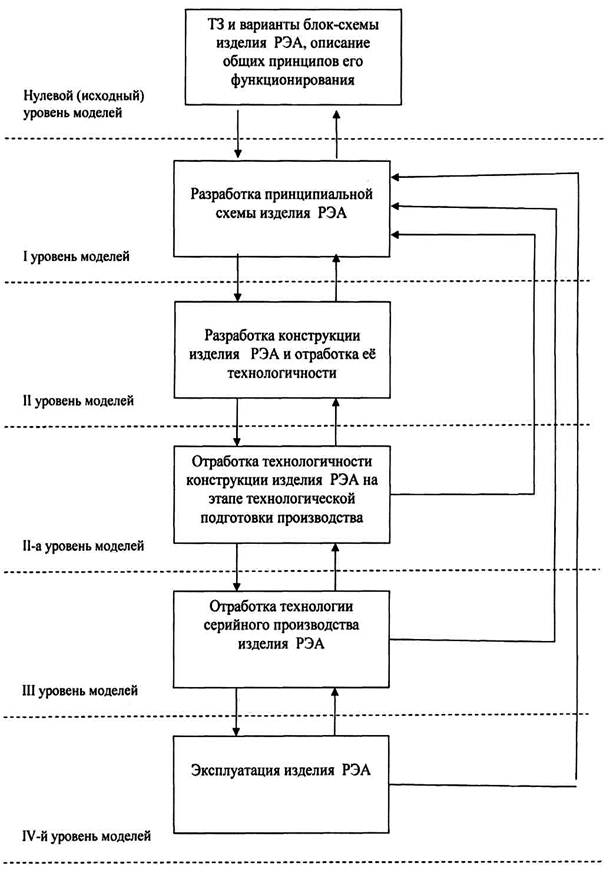
... приведен полный перечень и расчетные формулы используемых для оценки ТК РЭА количественных показателей. 3.2 Разработка информационного обеспечения системы показателей эффективной организации управленческого труда в организации и технологичности конструкции изделий и их составных частей Стандартами ЕСТПП введена система количественных оценок технологичности конструкций, охватывающая всю ...
0 комментариев