Навигация
Понятие и типы моделей сложных систем
2.7. Понятие и типы моделей сложных систем.
Моделью называется отображение определенных характеристик объекта
с целью его изучения (или управления). Модель позволяет выделить из
всего многообразия проявлений изучаемого объекта лишь те, которые не-
обходимы с точки зрения решаемой проблемы, т.е. модель - отражение
лишь определенной части его свойств. Поэтому, основной проблемой моде-
лирования является разумное упрощение модели, т.е. выбор степени подо-
бия модели и объекта.
Модели могут быть реализованы как физическими, так и абстрактными
системами. Соответственно модели бывают физические и абстрактные. Фи-
зическими моделями являются макеты приборов и машин и электрические
модели объектов и явлений.
В абстрактных моделях описание делается на каком-либо языке,
удобном для исследования, описание на математическом языке называется
математической моделью.
Представление реального объекта как системы, использование сис-
темных понятий при его моделировании послужили методологической осно-
вой для ряда принципов исследования, объединенных общим названием -
системный анализ. Каждую систему можно исследовать в 2-х аспектах: как
элемент более широкой системы и как совокупность взаимосвязанных эле-
ментов, эти два аспекта и определяют микроанализ - изучение и модели-
рование структуры и свойств элементов системы (предполагается, что это
доступно для наблюдения) и макроанализ - изучение системы в целом в ее
свойствах, поведении, взаимодействии с окружающей средой. Метод черно-
го ящика предполагает, что внутренняя структура системы неизвестна, а
наблюдаемы лишь связи системы с внешней средой.
Для разработки систем управления технологическим оборудованием и
процессами необходимо знать количественную зависимость между воздейс-
твиями на объект управления со стороны внешней среды и устройства уп-
равления и состоянием интересующих нас параметров объекта. Эта зависи-
- 59 -
мость может быть выражена в виде аналитических формул и уравнений,
схемы набора для аналоговой вычислительной машины, некоторой электри-
ческой цепи, описываемой теми же уравнениями, макета объекта.
В зависимости от цели исследования объекта могут строиться раз-
личные его модели. Так, при исследовании влияния размещения пассажиров
на центровку самолета моделью человека может служить мешок с песком,
для конструктора одежды - манекен, для медико-биологических исследова-
ний - животное.
Модель - специфическая форма отражения, при которой отображаются
свойства и закономерности объектов, существенно важные в данном произ-
водственном процессе. Отражаются свойства не все, а только связанные с
интересующим нас процессом. В отличие от образа, который является от-
ражением совокупности свойств предмета в нашем сознании, модель есть
отражение одного свойства или узкой группы свойств предмета и явления,
необходимых для решения определенной практической задачи, для предска-
зания результатов возможных решений, принимаемых человеком в его прак-
тической деятельности.
Модель отражает функциональные свойства объекта и, как всякое от-
ражение, не является тождественной объекту, поэтому необходимо ввести
оценку, или критерий близости, т.е. соответствия модели данному объек-
ту. Критерий обычно формируется как функционал от разности реакций
объекта и модели на одни и те же воздействия. Критерий является число-
вой характеристикой данной модели, представляет собой "штраф" за рас-
хождение реакций объекта и модели на одинаковые воздействия. По крите-
рию выбирается оптимальная модель из некоторого класса моделей. Модель
считается оптимальной, если для нее значение критерия минимальное.
Критерий зависит при этом от типа входного воздействия. Чтобы избежать
неопределенности, критерий формируют как результат усреднения разности
реакций модели и объекта по множеству входных сигналов и по времени.
Математические и физические модели. Первоначально понятие физи-
ческой модели развилось из понятия физического аналога, например,
уменьшенной копии объекта. Оказалось, что многие процессы различной
физической природы описываются одинаковыми уравнениями движения, нап-
ример, колебания груза на пружине, струны, тока в колебательном конту-
ре. Следовательно, движение объекта одной физической природы может
служить описанием движения объекта другой природы. Таким образом, фи-
зическая модель отделяется от материального носителя и возникает мате-
матическая модель как формулировка закона движения, совокупность урав-
нений, отражающих функциональные характеристики объекта.
Носителем математической модели помимо формул, программ для ЭВМ и
схем набора для АВМ могут служить и другие физические устройства, ко-
торые описываются известными уравнениями. Таким образом, происходит
смещение понятий - отделение физической модели от конкретного матери-
ального носителя, когда одна и та же модель может быть реализована в
устройствах различной физической природы, а математическая модель воп-
лощается в конкретном материальном устройстве. Различие физической и
математической модели носит чисто гносеологический характер.
МОДЕЛЬ называется математической, если известно ее математическое
описание. При этом модель может быть реализована в виде материального
устройства. Модель называется физической, если ее математическое опи-
сание неизвестно, но реакции модели схожи с реакциями объекта.
Точность модели определяется, с одной стороны, нашими знаниями о
процессах, происходящих в объектах, а с другой стороны, нашим умением
анализировать сложные модели, т.е. развитием математического аппарата
для исследования динамики процессов управления.
Наиболее разработаны методы исследования линейных дифференциаль-
ных уравнений с постоянными коэффициентами. Именно поэтому чаще всего
в качестве моделей принимаются линейные стационарные звенья. Следова-
- 60 -
тельно, для исследования динамики систем управления технологическими
объектами исключительное значение имеет выбор класса моделей объектов,
если же результаты расчета систем управления на основе выбранной моде-
ли существенно отличаются от результатов экспериментальной проверки,
то это свидетельствует о грубости модели и необходимости замены ее бо-
лее тонкой, сложной моделью и, следовательно, применении более сложных
и трудоемких математических методов. Аналогична ситуация и для физи-
ческой модели, где стремление к точности вступает в противоречие с
техническим уровнем эксперимента и возможностями экспериментатора.
Одна и та же модель может быть удовлетворительна для решения од-
них задач и совершенно неудовлетворительна для других. Например, пря-
моугольная ломаная, аппроксимирующая кривую намагничивания магнитомяг-
кого ферромагнитного материала, вполне приемлема для расчета магнитных
усилителей без обратной связи, но совершенно не годится для расчета
усилителей с внутренней положительной обратной связью.
Отметим еще одно противоречие модели объекта управления. Модель
оценивают по сходству ее с реакциями объекта на одни и те же воздейс-
твия. Этими воздействиями являются управляющие сигналы с регулятора.
Может оказаться, что при одних входных сигналах меньшее значение штра-
фа за несовпадение будет у одной модели, а при других входных воздейс-
твиях - у другой модели. Например, модель А точнее описывает реакции
объекта на низкочастотные сигналы, а модель Б - на высокочастотные.
Следовательно, значение критерия оценки качества модели зависит
от закона распределения управляющего сигнала, а последний - от пара-
метров и структуры регулятора. Однако модель создается именно для то-
го, чтобы с ее помощью выбрать регулятор и определить управляющие воз-
действия на объект.
Таким образом, выбор модели должен предшествовать выбору закона
управления, а выбор закона управления - выбору модели. Разрешить это
противоречие возможно методом последовательных приближений. Вначале
выбирается модель первого приближения на основе теоретического анализа
процессов в объекте. По этой модели выбираются параметры регулятора.
Затем подбирается модель второго приближения в эксперименте, где ис-
пользуется выбранный регулятор. По уточненной модели уточняются пара-
метры регулятора. Модели используются для нахождения законов управле-
ния, моделирования процессов с целью проверки законов управления,
оценки состояния. Различные задачи требуют различной детализации моде-
ли и их различных классов. Так, для синтеза законов управления при
современном уровне теории предпочтительнее линейные модели, а для мо-
делирования процессов и оценивания состояний средствами вычислительной
техники предпочтительны более сложные модели.
Построение моделей на основе анализа физико-химических процессов
в технологическом объекте. Такое построение позволяет составить урав-
нение даже на стадии проектирования объекта. Метод предполагает знание
тепловых, гидравлических, пневматических, электрических систем объек-
та, а также процессов массотеплопереноса и химических реакций.
Можно выделить общие подходы к составлению уравнений объектов.
Прежде всего следует расчленить мысленно объект на части и составить
уравнения для каждого узла, заменив отброшенные части системы эквива-
лентными воздействиями.
Например, уравнение динамики инфракрасной печи получается на ос-
нове законов теплообмена между нагревателями, теплоизоляцией (реакто-
ром) и объектом, установленным для термообработки в печи. В уравнении
участвуют составляющие теплообмена путем излучения, конвекции и теп-
лопроводностью. Коэффициенты уравнения зависят от таких физических ха-
рактеристик, как теплоемкость материала, излучательная способность,
температура окружающей среды, от геометрических размеров. В результате
упрощения записи уравнения теплообмена и пренебрежения членами высших
- 61 -
порядков, получается линеаризованное дифференциальное уравнение с пос-
тоянными коэффициентами, которое справедливо при небольших изменениях
приращений тепла, участвующего в массообмене.
В некоторых случаях линеаризация уравнения не позволяет адекватно
описывать объект, тогда используются нелинейные уравнения. Решение та-
ких уравнений представляет существенные проблемы и, в конечном итоге,
при решении таких систем все равно приходится проводить линеаризацию,
но только на уровне численных методов. Если объект описывается систе-
мой дифференциальных уравнений в частных производных, то решение такой
системы осуществляется с помощью численных методов, что, как уже ука-
зывалось выше, тоже линеаризация, только на более поздней стадии полу-
чения решения.
В том случае, если связи между входными и выходными параметрами
описать в виде дифференциального уравнения сложно (например, ввиду
слабой изученности природы объекта или влияние на выходные значения
параметров оказывают как физические, так и химические факторы, которые
составляют нерешаемую в данное время систему уравнений), используют
регрессионные модели - уравнения регрессии. В уравнениях такого вида и
используется принцип "черного ящика". Пусть связь между воздействием
х, управляющим технологическим процессом и переменной y, характеризую-
щей протекание этого процесса, выражается зависимостью y =f(х) (62),
которая заранее неизвестна. Требуется определить эту зависимость по
имеющимся экспериментальным данным. Иными словами, задача состоит в
том, что по имеющейся совокупности входных воздействий x 4i 0, i=1,...,n,
и соответствующих им выходных переменных y 4i 0, полученной в результате
эксперимента, определить вид зависимости y =f^(x), наилучшим образом
отражающей зависимость (62).
Эту задачу можно решить путем построения интерполяционного поли-
нома степени n-1, в точности проходящего через точки x 4i 0,y 4i 0 (известно,
что такой полином всегда существует). Однако на практике такое решение
оказывается неприемлемым ввиду того, то измерение значений происходит
с ошибками, поэтому построенный таким образом полином будет не столько
характеризовать объективную зависимость между величинами х и у, сколь-
ко характер ошибок измерения.
Таким образом, при построении модели процесса оказывается необхо-
димым отразить вид зависимости между входом и выходом, сгладив незако-
номерные случайные отклонения входной величины. Предположим, что эти
отклонения происходят по нормальному закону распределения с нулевым
средним (на практике это предположение обычно выполняется). Тогда y 4i
представляет собой случайные величины, распределенные по нормальному
закону с математическими ожиданиями f(x 4i 0) и дисперсиями s 4i 52 0, характе-
ризующими ошибки измерения. Предположим, что точность измерений во
всех точках одинакова, т.е. s 41 0=s 42 0=...=s 4n 0=s. Тогда плотность распреде-
ления вероятностей случайной величины y 4i
p 4i 0(y)=[1/(s- 7? 0(2 7p 0))]exp{[-y-f(x 4i 0) 52 0] /(2s 52 0)} (63).
Предположим, что в результате эксперимента происходит следующее
событие: случайные величины y 41 0,...,y 4n 0 принимают некоторые значения
y 41 0^,...y 4n 0^, равные результатам измерений. Задача заключается в том,
чтобы подобрать функцию f^(x) так, чтобы вероятность этого события бы-
ла максимальной. Для определения классов функций f^(x), в частности,
для функций, в которые искомые параметры входят линейно, при использо-
вании метода наименьших квадратов оказывается возможным определить не
только значения этих параметров, но и их важнейшие статистические ха-
рактеристики. Суть метода наименьших квадратов заключается в следую-
щем: функция f^(x) должна быть выбрана так, чтобы сумма квадратов отк-
лонений значений f^(x 4i 0) от измеренных значений y 4i 0^ была минимальной:
L= 7S 0[y^-f^(x 4i 0)] 52 0=min (64).
МНК обеспечивает идентификацию по принципу максимального правдо-
- 62 -
подобия при любом виде зависимости, связывающей входные воздействия и
выходные переменные процесса, этот метод работает в случае процессов
со многими входами и выходами, при использовании этого метода обычно
задаются видом функции f^(x) и в процессе идентификации (будет расс-
мотрено ниже), находят параметры, определяющие искомую функцию, кото-
рая удовлетворяет условию (64). Совокупность МНК и методов нахождения
этих статистических характеристик называется регрессионным анализом, а
сами модели - регрессионными моделями.
Простейшим примером регрессионной модели процесса с k входами
x 41 0,...,x 4k 0 и одним выходом y является уравнение y=a 41 0x 41 0+a 42 0x 42 0+...+a 4k 0x 4k 0+e
(65), где е - ошибки измерения.
Как видно из вышеизложенного, при построении модели объекта воз-
можно применение алгебраических методов, систем дифференциальных урав-
нений обычных и с частными производными и статистических методов -
регрессионого анализа, построенного на теории вероятности случайных
процессов и собственно сами методы теории вероятности.
Кроме статистических методов, уже достаточно хорошо отработанных,
в последнее время получили распространение методы нечетких (размытых)
множеств, особенно для непрерывных систем. Суть метода заключается в
следующем. Часто бывает необходимо формализовать качественную информа-
цию о процессе, который имеет большое количество факторов, влияющих на
его качество. Описание такого объекта системами уравнений в частных
производных не позволяет решить основную задачу - установить связь
между входом и выходом системы ввиду нерешаемости данной системы на
современном этапе развития вычислительной техники. При использовании
метода нечетких множеств вводятся отношения " больше", "меньше", "нам-
ного больше", "намного меньше", "чуть больше", "чуть меньше" и с по-
мощью этих отношений получают уравнение, которое решается известными
методами. Этот метод в своей сути имеет много общего с вероятностными
методами, где с определенной степенью допущения под соотношениями меж-
ду значениями переменных можно провести аналогию с вероятностью приня-
тия параметром того или иного значения.
При формализации качественной информации предполагается существо-
вание связи между нечетко определенными характеристиками и математи-
ческими объектами. Для таких параметров, как температура в технологи-
ческом агрегате, расход газообразного агента, давление, концентрация,
скорость движения среды и т.п. наличие такого соответствия очевидно. С
одной стороны, величине параметра ставится в соответствие числовая ко-
ордината с установленными на ней началом координат и мерой, а с другой
стороны - величину параметра описывают словесными высказываниями.
Пусть имеется множество Х параметров такого типа. Элементы x 4i 0сX,
обозначают названия параметров, например: температура, концентрация и
др. Количественной характеристикой x 4i 0 являются элементы u 4j 0сU. Множест-
во U представляет собой диапазон изменения параметров x 4i 0. При словес-
ном описании паре (x 4i 0,u 4j 0) ставится в соответствие нечеткий термин
q 4k 0сQ, Q- множество нечетких терминов. Иногда такого типа множества на-
зывают эмпирическими, т.е. множествами, элементы которых имеют не чис-
ловую природу. Примерами, как уже выше указывалось, являются такие не-
четкие термины как "высокий", "очень высокий", "низкий", "не очень
низкий" и др. Несмотря на то, что параметры такого типа могут быть из-
мерены, и их величина может быть выражена в числовом виде, на практике
это не всегда возможно в виду, например, агрессивности среды или очень
высокими значениями температур. В этом случае для получения количест-
венных характеристик может быть использована качественная информация,
прошедшая предварительную формализацию и адаптацию.
Существование словесных описаний параметров, которыми характери-
зуют качество вырабатываемой продукции. Здесь под качеством понимается
интегральная характеристика, которая складывается из ряда взаимосвя-
- 63 -
занных между собой компонентов, часть которых в отдельности не измеря-
ется методами количественного анализа, а контролируется визуально че-
ловеком. Примером такой характеристики является качество изделий из
стекла, которое оценивают по оптическим искажениям. На эту оценку су-
щественно влияют геометрия поверхности стекла, метод оценки, субъекти-
визм контролера. Потребность формализации качественной информации дик-
туется необходимостью решения следующих задач:
1. исключения субъективизма в оценках качества изделий;
2. разработки методов и технических решений для автоматической
классификации изделий;
3. нахождения взаимосвязей между показателями качества и техноло-
гическими параметрами. Чаще всего параметры данного типа не имеют
строго обоснованного математического аналога. Для их формализации при-
меняют метод экспертных оценок. Суть его заключается в выявлении мно-
жества нечетко определенных характеристик Q и сопоставлении его с мно-
жеством, имеющим числовую природу. Обычно выделяют следующие отношения
между рассматриваемыми объектами:
1. принадлежность к общему классу;
2. выражение порядка между объектами (например, параметр х 41 0 более
значим, чем х 42 0);
3. отношение эквивалентности в смысле принадлежности к общему
классу;
4. отношение порядка в системе. Названия параметров, между кото-
рыми устанавливается взаимосвязь, должны быть качественно совместимы в
смысле используемых отношений. В противном случае отношения между па-
раметрами могут не выполняться или потеряют смысл. Такая совместимость
обеспечивается на этапе качественного анализа исследователем.
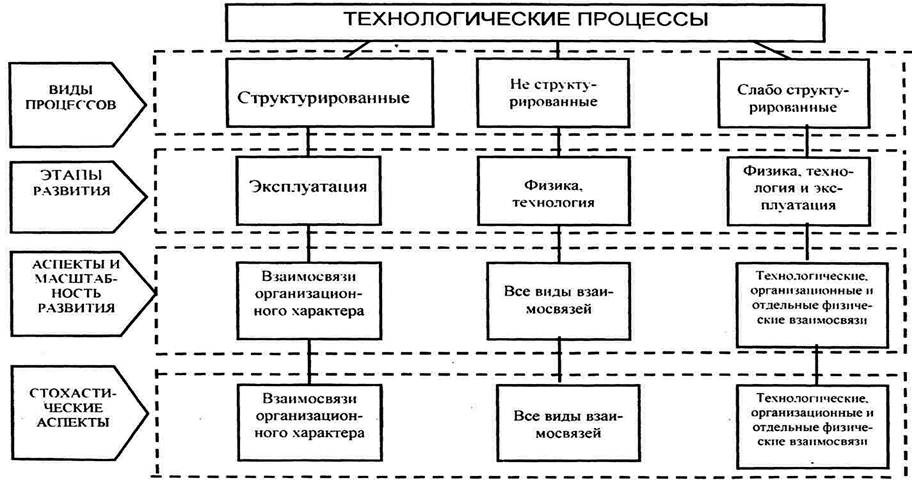
Для описания модели поведения дискретных систем разработана тео-
рия конечных автоматов. Здесь допускается, что система имеет конечное
число состояний и из одного состояния в другое может переходить при
определенных условиях (ограничениях). Математический аппарат, применя-
емый в этом методе - теория множеств.
Похожие работы
... гарантійного ремонту). В конструкції кришки для цього передбачено пломбувальний "стакан", що під час складання виробу на виробництві заповнюється пломбувальною пастою перед загвинчуванням гвинта. 2.2 Технологічний аналіз елементної бази В своєму складі блок живлення БП-9/4 має таку елементну базу: мікросхема, транзистор, діоди, конденсатори, резистори постійні та змінні. Усі перелічені ЕРЕ ...
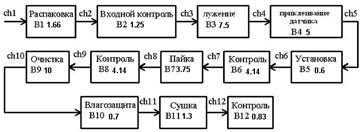
... выполнения норм времени, принимаем равным 1. Результаты расчета показателей поточной линии сборки приведены в таблице 1.2. Маршрутное описание технологического процесса производства модуля сопряжения цифрового мультиметра с компьютером представлено в приложении в виде маршрутных карт. Таблица 1.2 – Результаты расчета показателей поточной линии сборки Операция Оборудование Производит
... 0mil 0.0deg (0.0mil,0.0mil) Flash"* Выполнив сверление отверстий в ПП, робот выполняет установку ЭРЭ. После установки ЭРЭ, плату отправляют на пайку волной припоя. 2 МОДЕЛИРОВАНИЕ ТЕХНОЛОГИЧЕСКОГО ПРОЦЕССА Моделирование – это метод исследования сложных систем, основанный на том, что рассматриваемая система заменяется на модель и проводится исследование модели с целью получения информации об ...
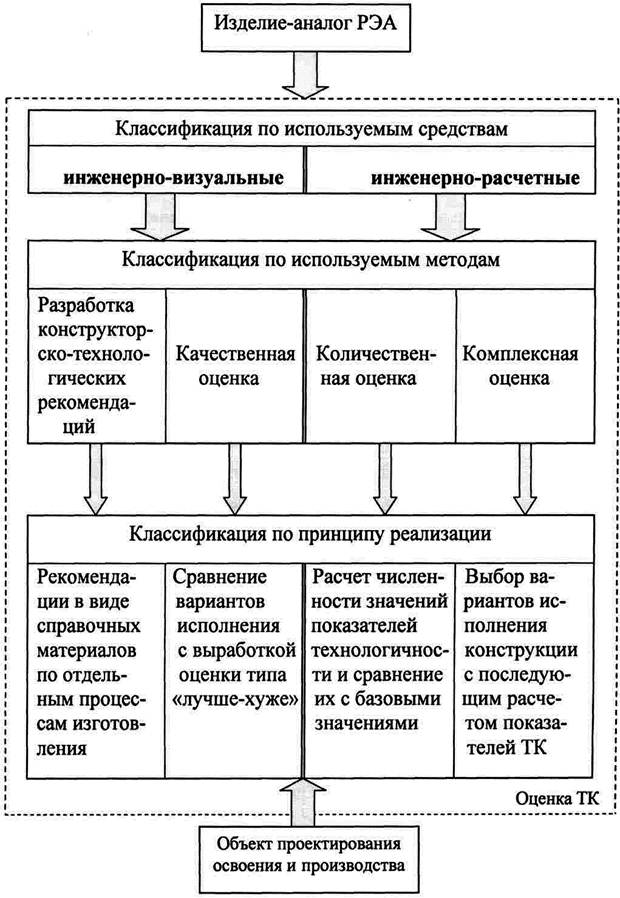
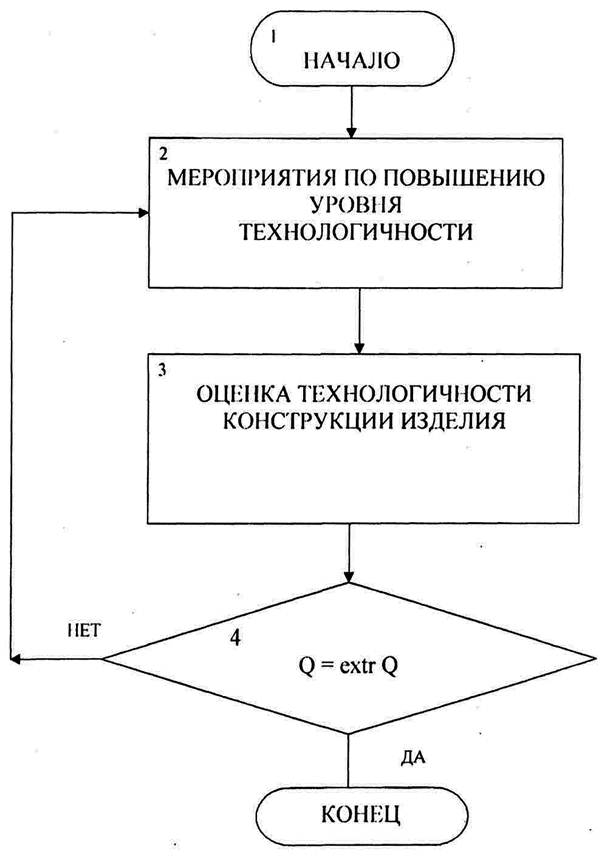
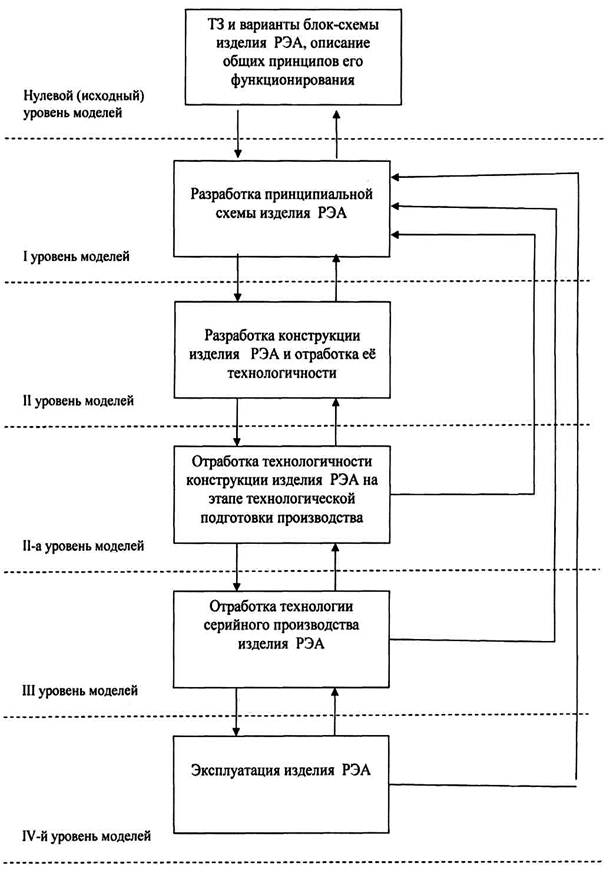
... приведен полный перечень и расчетные формулы используемых для оценки ТК РЭА количественных показателей. 3.2 Разработка информационного обеспечения системы показателей эффективной организации управленческого труда в организации и технологичности конструкции изделий и их составных частей Стандартами ЕСТПП введена система количественных оценок технологичности конструкций, охватывающая всю ...
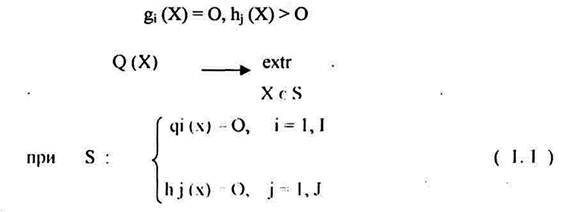
0 комментариев