Навигация
Устойчивость линейных САР. Если какое-либо решение линейного
1. Устойчивость линейных САР. Если какое-либо решение линейного
дифференциального уравнения с постоянными коэффициентами асимптотичес-
ки устойчиво, то асимптотически устойчиво любое его решение. Поэтому в
случае непрерывных линейных стационарных систем, т.е. систем, описыва-
емых линейными дифференциальными уравнениями с постоянными коэффициен-
тами, можно рассматривать их устойчивость, не указывая конкретного
движения. Непрерывная линейная стационарная САР называется устойчивой,
если асимптотически устойчиво какое-либо ее невозмущенное (заданное)
движение.
Если заданы внешние воздействия, то уравнение линейных стационар-
ных САР можно представить в виде (A 4o 0P 5n 0+A 41 0P 5n-1 0+...+A 4n 0)x=F(t) (55). В
уравнении A 4i 0, i=0,1,...,n - заданные постоянные коэффициенты, F(t) -
заданная функция времени. Общее решение уравнения имеет вид
X(t)=X 4в 0(t)+X 4c 0(t) (56), где X 4в 0(t) - частное решение неоднородного урав-
нения, X 4c 0(t) - общее решение однородного уравнения
- 57 -
(A 4o 0P 5n 0+A 41 0P 5n-1 0+...+A 4n 0)X=0 (57). Частное решение X 4в 0(t) определяет вынуж-
денное движение, решение X 4c 0(t) - свободное движение, т.е. движение,
которое, не зависит от внешних воздействий и определяется только на-
чальными условиями.
Невозмущенное движение задается внешним воздействием и при от-
сутствии внешних возмущающих воздействий совпадает с вынужденным дви-
жением X 4в 0(t). Поэтому линейная система устойчива, когда limX 4c 0(t)=0.
Это соотношение можно принять за определение устойчивости t->oo
линейных непрерывных систем.
Характеристическое уравнение. Устойчивость линейной системы, т.е.
выполнение условия, зависит от ее характеристического уравнения
A 4o 0L 5n 0+A 41 0L 5n-1 0+...+A 4n 0=0 (58). Левая часть характеристического уравнения
называется характеристическим полиномом. Характеристический полином
системы (с точностью до постоянного множителя и обозначений перемен-
ной) совпадает с ее собственным оператором и знаменателем ее переда-
точной функции. Характеристический полином замкнутой системы также ра-
вен (при отрицательной обратной связи) сумме P(p)+Q(p) полиномов чис-
лителя и знаменателя передаточной функции W(p)=P(p)/Q(p) (59) разомк-
нутой системы. Необходимое и достаточное условие устойчивости опреде-
ляется по корням характеристического уравнения. Если L 4i 0, i=1,...,q -
корни характеристического уравнения кратности k 4i 0, то общее решение од-
нородного уравнения имеет вид X 4c 0(t)= 7S 0Q 4i 0(t)e 5lit 0 (60), где
Q 4i 0(t)=C 41 5(i) 0+...+C 4ki 5(i) 0 - постоянные интегрирования. В частном случае,
когда все корни l 4i 0, i=1,...,n, простые, решение такого: X 4c 0(t)= 7S 0C 4i 0e 5lt
(61).
Свободное движение при t 76$ 0 стремится к нулю при произвольных пос-
тоянных интегрирования в том случае, когда все корни характеристичес-
кого уравнения имеют отрицательные вещественные части. Таким образом,
для того, чтобы линейная непрерывная система была устойчива, необходи-
мо и достаточно, чтобы все корни ее характеристического уравнения име-
ли отрицательные вещественные части: Rel 4i 0<0, i=1,...,q.
Необходимое условие устойчивости. Для того, чтобы система была
устойчива, необходимо, чтобы коэффициенты ее характеристического урав-
нения были одного знака: A 4o 0>0,...,A 4n 0>0 или A 4o 0<0,...,A 4n 0<0. Если необхо-
димое условие не выполняется, система неустойчива.
Критерий Гурвица. Для того, чтобы система была устойчива, необ-
ходимо и достаточно, чтобы все определители Гурвица, составленные из
коэффициентов ее характеристического уравнения, были больше нуля. Это
алгебраический критерий устойчивости.
2. Устойчивость нелинейных САР.
САР называется нелинейной, если она описывается нелинейными урав-
нениями. Линейные системы являются идеализированными моделями реальных
САР. Если нелинейность допускает обычную линеаризацию, то такая нели-
нейность называется несущественной. В противном случае нелинейность
называется существенной. Для нелинейных систем несправедлив принцип
суперпозиции. В случае нелинейных систем из устойчивости какого-либо
невозмущенного движения не следует устойчивость любого возмущенного
движения: одни возмущенные движения могут быть устойчивы, а другие
нет. Кроме того, не любое возмущенное движение при t 76$ 0 стремится к
асимптотически устойчивому невозмущенному движению.
Вид кривой переходного процесса в линейных системах не зависит от
величины начального отклонения. В нелинейных системах кривые переход-
ного процесса, соответствующие различным начальным отклонениям, могут
сильно отличаться. Более того, в зависимости от величины начального
отклонения от исходного состояния система может стремиться к разным
состояниям. В нелинейных системах наблюдаются такие установившиеся пе-
риодические режимы (автоколебания), которые в линейных системах невоз-
можны.
- 58 -
Универсальных методов исследования нелинейных систем нет. Имеются
различные методы, которые пригодны или удобны для решения определенно-
го класса задач. Довольно широко используются следующие методы: метод
фазового пространства, прямой метод Ляпунова, частотный метод Попова,
метод гармонической линеаризации и др. Суть метода фазового пространс-
тва заключается в построении параметрических уравнений фазовой траек-
тории с целью получения фазового портрета. По фазовому портрету систе-
мы можно построить соответствующую кривую переходного процесса. Фазо-
вые портреты нелинейных систем могут содержать изолированные замкнутые
траектории, соответствующие периодическим режимам. Эти кривые называ-
ются предельным циклом. Если изнутри и снаружи фазовые траектории схо-
дятся к предельному циклу, то такой предельный цикл называется устой-
чивым. Устойчивому предельному циклу соответствует устойчивый периоди-
ческий режим (автоколебания). Если движение начинается внутри предель-
ного цикла, то процесс расходится, если вне - то сходится. Если фазо-
вые траектории изнутри и снаружи предельного цикла удаляются от него,
то такой предельный цикл называется неустойчивым.
Метод гармонической линеаризации разработан и обоснован для исс-
ледования периодических режимов. Этот метод является приближенным и
применим, если линейная часть, которая следует за нелинейным элемен-
том, обладает свойством фильтра низких частот. Сущность метода заклю-
чается в том, что система представляется в виде линейной и нелинейной
части. Делается допущение о наличии в системе колебательного режима,
пренебрегаются высшие гармоники и выходной сигнал представляется в ви-
де ряда Фурье и получается гармонизированная система вместо нелиней-
ной, которая и исследуется с использованием частотных характеристик.
Похожие работы
... гарантійного ремонту). В конструкції кришки для цього передбачено пломбувальний "стакан", що під час складання виробу на виробництві заповнюється пломбувальною пастою перед загвинчуванням гвинта. 2.2 Технологічний аналіз елементної бази В своєму складі блок живлення БП-9/4 має таку елементну базу: мікросхема, транзистор, діоди, конденсатори, резистори постійні та змінні. Усі перелічені ЕРЕ ...
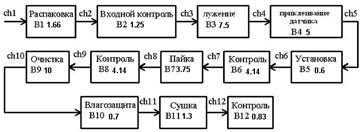
... выполнения норм времени, принимаем равным 1. Результаты расчета показателей поточной линии сборки приведены в таблице 1.2. Маршрутное описание технологического процесса производства модуля сопряжения цифрового мультиметра с компьютером представлено в приложении в виде маршрутных карт. Таблица 1.2 – Результаты расчета показателей поточной линии сборки Операция Оборудование Производит
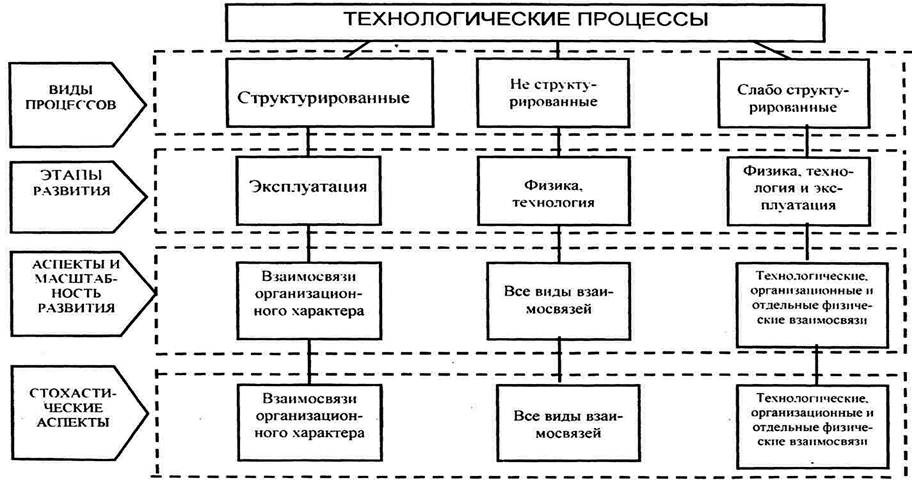
... 0mil 0.0deg (0.0mil,0.0mil) Flash"* Выполнив сверление отверстий в ПП, робот выполняет установку ЭРЭ. После установки ЭРЭ, плату отправляют на пайку волной припоя. 2 МОДЕЛИРОВАНИЕ ТЕХНОЛОГИЧЕСКОГО ПРОЦЕССА Моделирование – это метод исследования сложных систем, основанный на том, что рассматриваемая система заменяется на модель и проводится исследование модели с целью получения информации об ...
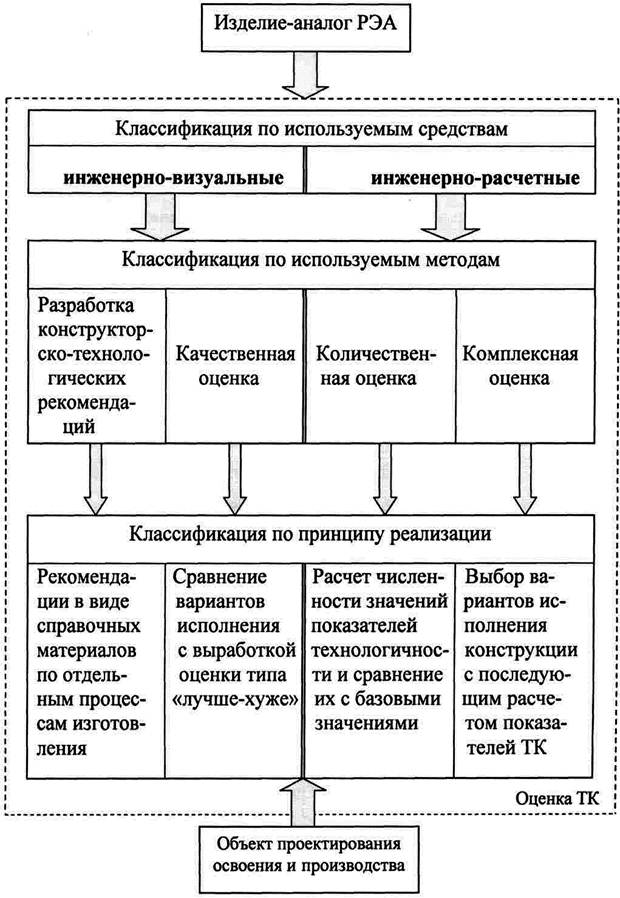
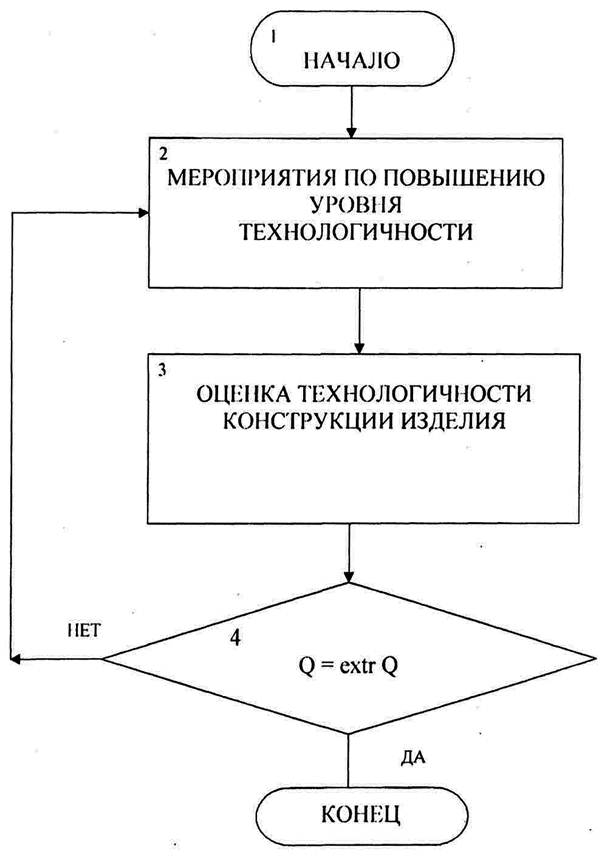
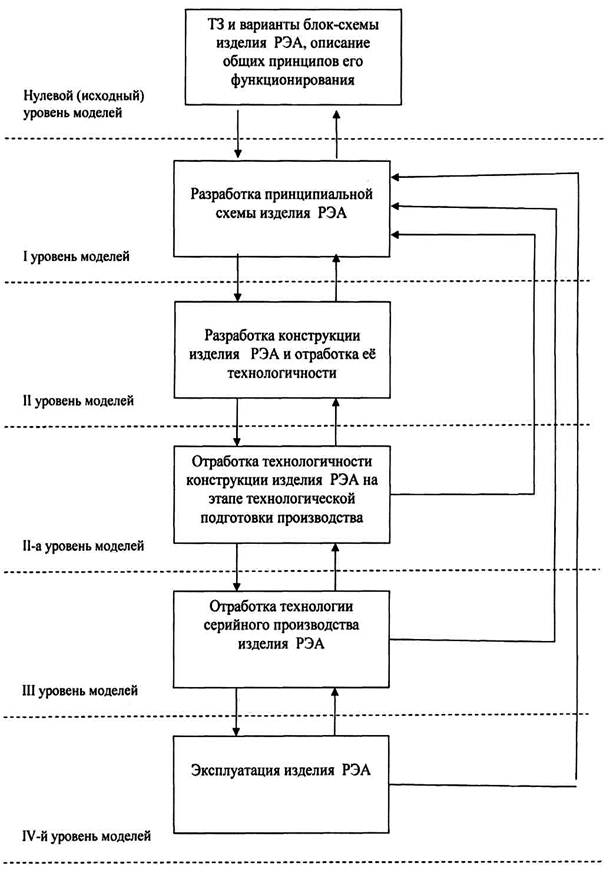
... приведен полный перечень и расчетные формулы используемых для оценки ТК РЭА количественных показателей. 3.2 Разработка информационного обеспечения системы показателей эффективной организации управленческого труда в организации и технологичности конструкции изделий и их составных частей Стандартами ЕСТПП введена система количественных оценок технологичности конструкций, охватывающая всю ...
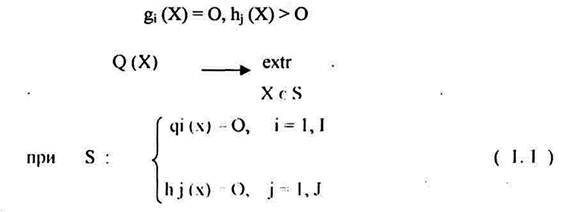
0 комментариев