Навигация
Основные понятия теории вероятности
3.3. Основные понятия теории вероятности.
Нормальное распределение, математическое ожидание,
дисперсия, среднеквадратическое отклонение.
Доверительный интервал.
Методы проверки гипотез о распределении.
Предметом теории вероятности является математический анализ слу-
чайных явлений, т.е. таких эмпирических феноменов, которые, при опре-
деленном комплексе условий, могут быть охарактеризованы тем, что для
них отсутствует детерминистическая регулярность (наблюдения за ними не
всегда приводят к одним и тем же результатам) и в то же время они об-
ладают некоторой статистической регулярностью (проявляющейся в статис-
тической устойчивости частот).
Смысл статистической устойчивости частот заключается в том, что,
если результаты отдельных наблюдений носят нерегулярный характер, то
большое количество экспериментов позволяют получить некоторые законо-
мерности, связанные с этими экспериментами. Статистическая устойчи-
вость частот делает весьма правдоподобной гипотезу о возможности коли-
чественной оценки "случайности" того или другого события А, осущест-
вляемого в результате экспериментов. Исходя из этого, теория вероят-
ности постулирует существование у события А определенной числовой ха-
рактеристики Р(А), называемой вероятностью этого события, естественное
свойство которой должно состоять в том, что с ростом числа "независи-
мых" испытаний (экспериментов) частота появления события А должна
приближаться к Р(А).
Частотой события называется отношение числа его появлений к числу
произведенных опытов. Таким образом, если в n опытах событие А появи-
лось m раз, то его частота равна m/n. lim(m/n)=P(A).
n 76$
Предположим, что в результате n опытов случайная величина Х при-
няла значения х 41 0,х 42 0,...,х 4n 0, тогда выборочное среднее определяется фор-
мулой: 4n 0 4n
х 4ср 0=( 7S 0x 4i 0)/n; lim(x 4ср 0)=M(X); d 5* 0=( 7S 0(x 4i 0-х 4ср 0) 52 0)/n; lim(d 5* 0)=D(X); где
5i=1 0 n 76$ 0 5i=1 0 n 76$
- 94 -
M(X) - математическое ожидание величины Х; d 5* 0 - выборочная дисперсия
величины Х; D(X) - дисперсия величины Х, корень квадратный из диспер-
сии называется среднеквадратическим отклонением величины Х.
Большое значение в теории вероятности, особенно при обработке ре-
зультатов экспериментов играет распределение Гаусса (нормальное расп-
ределение, нормальный закон, нормальная кривая, закон Гаусса), оно ха-
рактеризуется двумя параметрами: m 4x 0 - математическим ожиданием и s 4x 0 -
среднеквадратическим отклонением, которые полностью определяют все его
характеристики. При m 4x 0=0, s 4x 0=1 f(x)=(2 7p 0) 5-1/2 0exp{-x 52 0/2 } (88) нормаль-
ная кривая называется нормированной.
──────────────────────────────────────────────────────────────────────
f(x)
m 4x 0=0 . m 4x 0=0 . . m 4x 0=1 s 4x 0=2
s 4x 0=2. /|\. s 4x 0=1. .
. . | . . / \
. . | . / . \
. .. . . . .|../. . . . . .
________________0_|__________1_____________ x
Рис. 12. Примеры нормального распределения.
──────────────────────────────────────────────────────────────────────
Как показывает практика, такое распределение характерно для расп-
ределения погрешностей устойчивых, стабильных технологических процес-
сов производства РЭА.
Любая функция результатов опытов, которая не зависит от неизвест-
ных статистических характеристик, называется статистикой. Оценкой ста-
тистической характеристики Q называется статистика, реализация кото-
рой, полученная в результате опытов, принимается за неизвестное истин-
ное значение параметра Q. Оценка называется состоятельной, если она
сходится по вероятности к Q при неограниченном увеличении числа опытов
n. Чтобы оценка была состоятельной, достаточно, чтобы ее дисперсия
стремилась к нулю при неограниченном увеличении числа опытов n.
Случайный интервал, полностью определяемый результатами опытов и
независящий от неизвестных характеристик, который с заданной вероят-
ностью а накрывает неизвестную скалярную статистическую характеристику
Q, называется доверительным интервалом для этой характеристики, соот-
ветствующим коэффициенту доверия а. Величина 1-а называется уровнем
значимости отклонения оценки. Концы доверительного интервала называют-
ся доверительными границами.
Как показывает практика, распределение случайной величины невоз-
можно точно определить по результатам опытов. Полученные эксперимен-
тальные результаты дают возможность только строить различные гипотезы
о распределении случайной величины, например, гипотезу о том, что она
распределена нормально. Поэтому возникает задача проверки гипотез. Эта
задача состоит в том, чтобы определить, насколько согласуется та или
иная гипотеза о распределении случайной величины с полученными экспе-
риментальными данными. Эта задача тесно связана с задачей определения
доверительных областей для плотности или функции распределения. Однако
она имеет следующие особенности. Проверяя гипотезу о нормальном расп-
ределении, по той же выборке обычно оценивают математическое ожидание
и ковариационную матрицу (дисперсию в случае одномерного распределе-
ния) случайной величины. Вследствие этого гипотетическое распределение
оказывается само случайным - функцией случайных результатов опытов.
Это и отличает задачу проверки гипотез о распределении от задачи опре-
деления доверительных областей для распределений. И только в отдельных
случаях может возникнуть задача проверки гипотезы о том, что случайная
величина подчинена вполне определенному закону распределения, не зави-
сящему от неизвестных параметров.
Для проверки гипотез о распределении применяются различные крите-
- 95 -
рии согласия. Наиболее удобным и универсальным критерием является кри-
терий 7c 52 0 (хи-квадрат) К.Пирсона. Он совершенно не зависит от распреде-
ления случайной величины и от ее размерности. Критерий Пирсона основан
на использовании в качестве меры отклонения экспериментальных данных
от гипотетического распределения той же величины, которая служит для
построения доверительной области для неизвестной плотности, с заменой
неизвестных истинных значений вероятностей попадания в интервалы веро-
ятностями, вычисленными по гипотетическому распределению.
Посмотрим использование статистического метода на примере статис-
тического анализа производственных погрешностей. Данный метод анализа
позволяет устанавливать качественные взаимосвязи факторов, вызывающих
производственные погрешности, учитывать характер их влияния на суммар-
ную погрешность. Статистический анализ делят на два этапа. Первым эта-
пом является конкретный анализ исследуемого процесса, а вторым - выбор
объектов исследования, определение объема экспериментов и назначение
средств технического контроля. Средства технического контроля (измери-
тельные средства) должны выбираться такими, чтобы соотношение между
предельными погрешностями измерения и заданным допуском на определен-
ный параметр качества было порядка 1:10 и даже 1:20. Точные измери-
тельные средства назначаются для обеспечения надежности выводов. Необ-
ходимо тщательно соблюдать одни и те же условия проведения опытов и
измерений.
Непосредственно за этими подготовительными работами следует:
1. собственно наблюдения изучаемого узла (измерение параметров,
определение свойств и т.п.);
2. группировка полученного при наблюдениях статистического мате-
риала;
3. сводка результатов наблюдения и вычисление параметров распре-
деления изучаемого узла;
4. анализ параметров распределения изучаемого узла.
Изменение значений параметров деталей, узлов и т.д., колеблющихся
в определенных пределах, называется вариацией, а ряд значений парамет-
ров для всей партии выборки деталей - вариационным рядом. Этот ряд от-
ражает закономерность соответствующего технологического процесса. Ва-
риационный ряд, выраженный графически, позволяет получить кривую расп-
ределения производственных погрешностей параметров изучаемого узла.
Однако, вычисление характеристик распределения погрешностей проще
и удобнее производить не по данным вариационного ряда, а по данным,
предварительно сгруппированным в интервале значений интересующего нас
параметра. Возникает необходимость перехода от вариационного к интер-
вальному ряду распределения погрешностей. По протоколу измерения пара-
метров деталей находят два значения, соответствующие максимальным
крайним отклонениям от номинала, т.е. Х 4макс 0 и Х 4мин 0. Используя эти зна-
чения, находим размах варьирования: R=Х 4макс 0-Х 4мин 0 (89). Для перехода к
интервальному ряду необходимо определить количество интервалов и их
ширину. Количество интервалов выбирают таким, чтобы на каждый интервал
в среднем приходилось не менее 10 значений из общего количества наблю-
дений исследуемого параметра, т.е. р=0,1n. Ширина интервала определя-
ется из выражения: dx=R/(0,1n -1) (90), где n - количество деталей в
исследуемой партии.
При определении границ интервалов рекомендуется начинать ряд со
значения, величина которого на 0,5 интервала меньше Х 4мин 0 и заканчивать
ряд величиной, которая превышает Х 4макс 0 также на 0,5 интервала. Границы
и средние значения интервала распределения записываются в форме табли-
цы 5.
Частота заполняется по данным протокола измерений с разнесением
всех частных значений исследуемого параметра по соответствующим интер-
валам. Количество значений исследуемого параметра, попавших в тот или
- 96 -
Таблица 5
┌────────┬────────────────────────────┬──────────────┬──────┬────────┐
│n интер-│Границы интервалов │Середина ин- │часто-│частость│
│вала │ │тервала │та mj │mj/n │
├────────┼────────────────────────────┼──────────────┼──────┼────────┤
│ 1 │Х 4мин 0-0,5dх - Х 4мин 0+0,5dх │Х 4мин 0 │ m 41 0 │ m 41 0/n │
│ 2 │Х 4мин 0+0,5dх - Х 4мин 0+1,5dх │Х 4мин 0+dх │ m 42 0 │ m 42 0/n │
│ 3 │Х 4мин 0+1,5dх - Х 4мин 0+2,5dх │Х 4мин 0+2dх │ m 43 0 │ m 43 0/n │
│........│............................│..............│......│........│
│ р │Х 4макс 0-0,5dх - Х 4макс 0+0,5dх │Х 4макс 0 │ m 4p 0 │ m 4p 0/n │
├────────┼────────────────────────────┼──────────────┼──────┼────────┤
│ 7S 0 │Х 4мин 0-0,5dх - Х 4макс 0+0,5dх │(Х 4мин 0+Х 4макс 0)/2│ n │ 1 │
└────────┴────────────────────────────┴──────────────┴──────┴────────┘
иной интервал, составляет частоту m 4j 0. Соотношение m 4j 0/n называется час-
тостью и представляет собой частость значений исследуемого параметра и
определяется для каждого интервала как отношение количества и значений
интересующего нас параметра, попавших в данный интервал к общему коли-
честву значений параметра в исследуемой партии. Контроль правильности
заполнения граф по частотам и частостям производится суммированием
заключенных в них значений по всем интервалам. При этом сумма частот
должна быть равна n, а сумма частостей - единице.
Таким образом, исходный вариационный ряд, представляющий собой
результаты измерения параметров изделий (деталей или узлов) в коли-
честве n шт., заменяют интервальным рядом распределения, включающим в
конечном счете всего р значений (по числу интервалов) варьирующего
признака.
Для большей наглядности прибегают к графическому изображению ин-
тервальных рядов распределения в виде гистограммы или полигона. Пост-
роение интервального ряда в виде гистограммы основано на предположе-
нии, что плотность частоты (частости) остается постоянной внутри каж-
дого интервала и меняется скачками на краях интервалов. Строится гис-
тограмма следующим образом: на оси абсцисс откладываются интервалы
значений исследуемого параметра, над каждым из которых строится прямо-
угольник, площадь которого пропорциональна частоте (частости) в этом
интервале. Т.к. все интервалы имеют одинаковую ширину, то высоты пря-
моугольников оказываются пропорциональными частотами или частостями.
──────────────────────────────────────────────────────────────────────
│ m/n X 4ср
│<─────────────>│
│< 1-янв-1980>┌─┼─┐
│номинал по ┌┤ │ │
│ ТУ ││ │ ├───┐
│ ││ │ │ │
│ ││ │ │ │
│ ┌───┤│ │ │ │
│ │ ││ │ │ │
│ │ ││ │ │ ├──┬─┐
│ ┌────┤ ││ │ │ │ │ │
└┬┬─┴────┴───┴┴─┴─┴───┴──┴─┴──┬─┬─────────────── X
0││ Х 4мин 0 Х 4макс 0 │ │
││<─────────────────────────>│ │
│ поле допуска по ТУ │
│<────────────────────────────>│
поле отклонений
Рис. 13. Гистограмма и полигон распределения погрешностей
──────────────────────────────────────────────────────────────────────
Принятое выше допущение для построения гистограммы безусловно
- 97 -
исключает реальный характер закона распределения погрешностей исследу-
емого параметра и тем сильней, чем больше длина интервала.
Более близким к действительности является предположение о равно-
мерном изменении плотности частоты или частости от интервала к интер-
валу. Такое суждение приводит нас к необходимости изображения интер-
вальных рядов в виде полигонов распределения. Для построения полигона
необходимо из середины каждого интервала провести ординаты, высота ко-
торых пропорциональна частотам или частостям, и концы ординат соеди-
нить ломаной линией.
Ординаты гистограмм и полигонов в более общем случае при неравных
интервалах представляют собой отрезки, пропорциональные плотности час-
тоты или частости. Что касается частот (частостей), то они изображают
площади прямоугольников на гистограмме и, следовательно, площадь тра-
пеции с ломаной вершиной на полигоне распределения погрешностей.
На этом же графике отмечены номинал исследуемого параметра и поле
допуска относительно номинала, а также среднее значение (центр распре-
деления) и поле отклонений, представляющее собой величину 7+ 0 s 4x 0, отло-
женного относительно среднего значения. Этот график позволяет делать
многие выводы о ходе технологического процесса и качестве выпускаемой
продукции:
- отклонение среднего значения от номинального показывает систе-
матическую погрешность настройки технологического оборудования;
- s 4x 0 характеризует случайную составляющую погрешности и ее срав-
нение с полем допуска позволяет сделать вывод о правильности выбора
точностных характеристик используемого оборудования и необходимости их
корректировок;
- отношение площади той части гистограммы, которая находится за
пределами поля допуска, к общей площади гистограммы позволяет оценить
долю брака в выпускаемой продукции.
Однако, с гистограммой работать не очень удобно, ее следует апп-
роксимировать. Для этого используется метод сплайн-интерполяции, кото-
рый заключается в использовании интервальных рядов. В этом методе
функция между каждыми двумя соседними точками аппроксимируется полино-
мом третьей степени: y=ax 53 0+bx 52 0+cx+d (91), а коэффициенты a, b, c, d
выбираются так, чтобы сходящийся в каждой точке "правый" и "левый" по-
лином имели равные первую и вторую производные. Другими словами, поли-
номы на отрезке [X 4мин 0,X 4макс 0] "сшиваются" по двум производным; в ре-
зультате получается единая гладкая кривая. Однако эта кривая еще не
является аппроксимацией функции плотности вероятности, поскольку еще
не выполнено условие нормирования. Поэтому следующим этапом является
вычисление интеграла:
Х 4макс 0-dx/2
J= 73 0f(x)dx (92)
X 4мин 0+dx/2
Если после вычисления произвести деление f(x) на J: w 5* 0(x)=f(x)/J (93),
то полученная функция будет иметь интеграл в в указанных пределах ин-
тегрирования равный единице и поэтому функция будет аппроксимировать
действительную плотность вероятности на отрезке, ограниченном пределом
интегрирования.
В качестве примера рассмотрим технологический процесс производс-
тва типовых элементов замены (ТЭЗов). Основным параметром, характери-
зующим качество, будем считать время наработки на отказ t 4o 0 в условиях
механических воздействий, которое, согласно техническим условиям, не
должно быть меньше t 4отмин 0. Следует решить задачу о серийнопригодности,
при этом, процент выхода годных ТЭЗов должен быть равен 90%. Решение
сводится к вычислению интеграла 7$
J= 73 0w(t 4o 0)dt 4от 0 (94),
t 4отмин
- 98 -
где w(t 4о 0) - функция плотности вероятности отказов. Если J>0,9, делает-
ся вывод о серийнопригодности ТЭЗа. Если нет, то можно предпринять
следующие корректирующие действия:
1. Можно снизить требование к проценту выхода годных, однако, как
следствие, возрастет стоимость продукции, поэтому такая мера приемлема
только в условиях мелкосерийного производства.
2. В крупносерийном или массовом производстве следует произвести
регулировку и настройку технологического оборудования, либо замену его
части с целью уточнения параметров технологического процесса; при этом
должен увеличиваться процент выхода годных.
Похожие работы
... гарантійного ремонту). В конструкції кришки для цього передбачено пломбувальний "стакан", що під час складання виробу на виробництві заповнюється пломбувальною пастою перед загвинчуванням гвинта. 2.2 Технологічний аналіз елементної бази В своєму складі блок живлення БП-9/4 має таку елементну базу: мікросхема, транзистор, діоди, конденсатори, резистори постійні та змінні. Усі перелічені ЕРЕ ...
... выполнения норм времени, принимаем равным 1. Результаты расчета показателей поточной линии сборки приведены в таблице 1.2. Маршрутное описание технологического процесса производства модуля сопряжения цифрового мультиметра с компьютером представлено в приложении в виде маршрутных карт. Таблица 1.2 – Результаты расчета показателей поточной линии сборки Операция Оборудование Производит
... 0mil 0.0deg (0.0mil,0.0mil) Flash"* Выполнив сверление отверстий в ПП, робот выполняет установку ЭРЭ. После установки ЭРЭ, плату отправляют на пайку волной припоя. 2 МОДЕЛИРОВАНИЕ ТЕХНОЛОГИЧЕСКОГО ПРОЦЕССА Моделирование – это метод исследования сложных систем, основанный на том, что рассматриваемая система заменяется на модель и проводится исследование модели с целью получения информации об ...
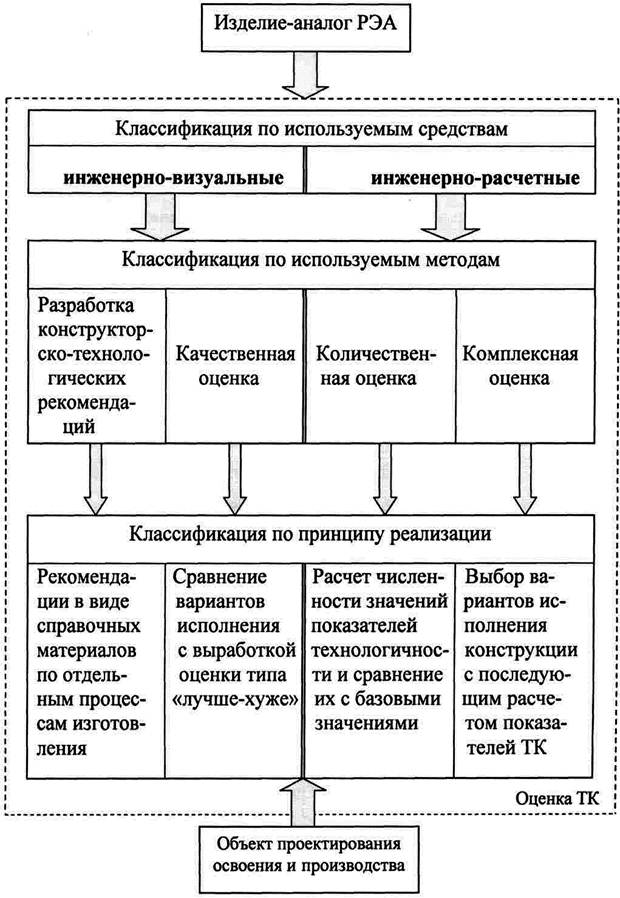
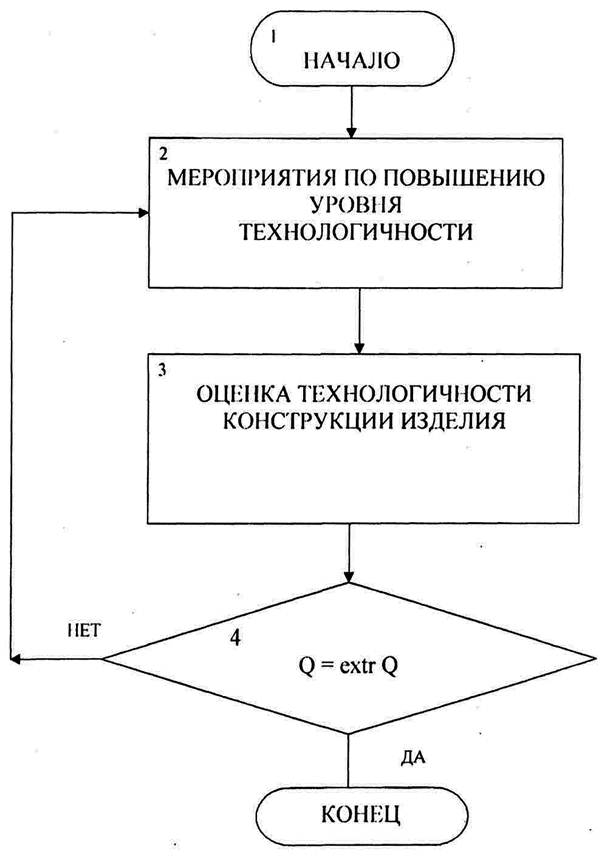
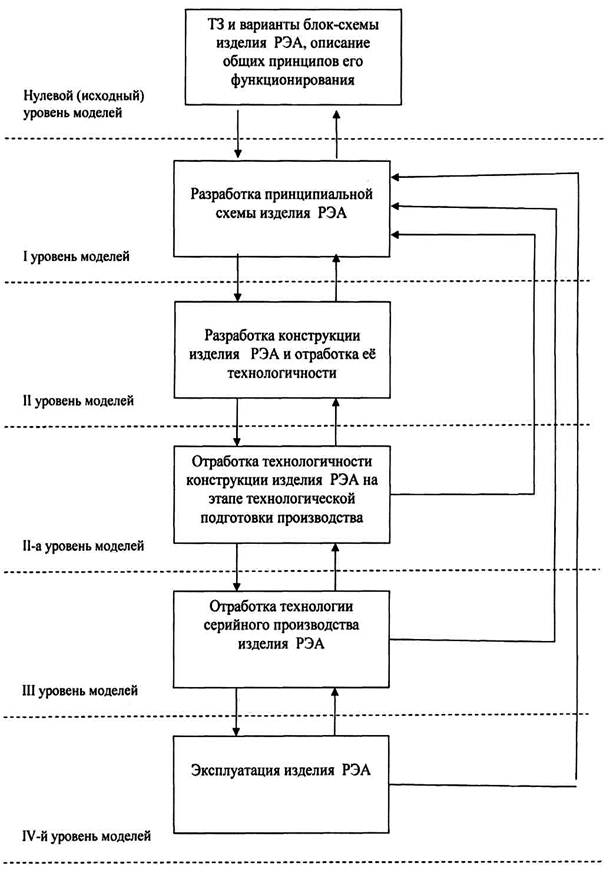
... приведен полный перечень и расчетные формулы используемых для оценки ТК РЭА количественных показателей. 3.2 Разработка информационного обеспечения системы показателей эффективной организации управленческого труда в организации и технологичности конструкции изделий и их составных частей Стандартами ЕСТПП введена система количественных оценок технологичности конструкций, охватывающая всю ...
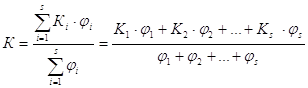
0 комментариев