Программное обеспечение ПК: классификация, назначение, краткая характеристика

115. Программное обеспечение ПК: классификация, назначение, краткая характеристика.

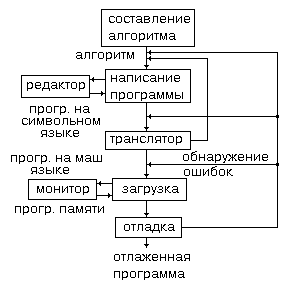
Состоит из операционной системы (ОС) и программ пользователя. ОС состоит из утилит, библиотеки подпрограмм, языковых трансляторов, программы – компоновщика, редактора, монитора, загрузчика.

Написание программы начинается с постановки задачи и с создания математической модели. Затем пишется алгоритм, который представляет собой пошаговую процедуру решения задачи. Программа пишется на языке высокого уровня. Языки высокого уровня не связаны с архитектурой данной машины.

Программа, написанная на языке высокого уровня называется исходным модулем. Программа - транслятор преобразует исходный модуль программу на языке машинных кодов называется объектным модулем. Машинный код для каждой машины свой. Программа - редактор используется для ввода текста программы в ЭВМ и ее последующего редактирования. Программа - компоновщик связывает объектные модули, являющиеся результатом трансляции программ и подпрограмм считанных из библиотеки подпрограмм. Программа - отладчик позволяет выполнять программу по одной или нескольким командам за один шаг, что позволяет программисту проверять результат выполнения отдельных частей программы.

Для ввода программы с клавиатуры или ВЗУ, используется программа, называемая загрузчиком. В ее функции входит операция чтения или записи по заданному адресу памяти, а так же выполнение работ по отладке и обслуживанию программ. В последнем случае программа - загрузчик называется монитором. Она может быть записана в память машины, тогда она называется резидентной. Выполнение загрузки программы в память начинается с передачи управления по первому адресу программы.

116. Постановка и математическая запись задачи линейного программирования.

Линейное программирование - это наука о методах исследования и

отыскания наибольших и наименьших значений линейной функции, на неизвестные

которой наложены линейные ограничения. Таким образом, задачи линейного программирования относятся к задачам на условный экстремум функции.

В настоящее время линейное программирование является одним из наиболее употребительных аппаратов математической теории оптимального принятия решений, в том числе и в финансовой математике. Для решения задач линейного программирования разработано сложное программное обеспечение, дающее возможность эффективно и надежно решать практические задачи больших объемов. Эти программы и системы снабжены развитыми системами подготовки исходных данных, средствами их анализа и представления полученных результатов. В развитие и совершенствование этих систем вложен труд и талант многих математиков, аккумулирован опыт решения тысяч задач. Владение аппаратом линейного программирования необходимо каждому специалисту в области прикладной математики.

Задача линейного программирования, которая является частным случаем задачи оптимизации записывается следующим образом: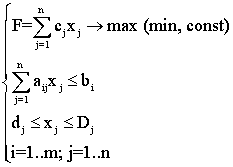
 

Дана система из n линейных неравенств с n неизвестными и линейная функция F. Требуется найти решение системы x₁, x₂, x₃…x_n, удовлетворяющей ГРУ, при котором функция F принимает max значение.

Задачи линейного программирования можно решить аналитическим путем и графическим методом. Второй метод - наглядный, но пригоден лишь для n=2 ( т.е. где число переменных = 2).

Пример

Известно, что уравнение прямой имеет вид: a₁x₁+a₂x₂=b. Построим прямую 2x₁+x₂=2. Перепишем это уравнение в виде:

При такой форме записи в знаменателе показаны отрезки, которые отсекает прямая на осях координат (Рис. 7.2). Если от исходного уравнения перейти к неравенству 2x1+x2≤2, то графически решение этого неравенства показано на рис. 7.3, т.е. решением линейного неравенства с двумя переменными является полуплоскость. На рис. 7.3 часть плоскости, которая не удовлетворяет неравенству расположена выше прямой, заштрихована. Координаты всех точек, принадлежащих не заштрихованной части плоскости, имеют такие значения х1 и х2, которые удовлетворяют заданному неравенству. Эта полуплоскость является областью допустимых решений (ОДР).

Рассмотрим систему неравенств:

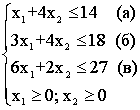
Для удобства запишем ее в следующем виде:

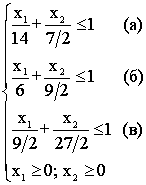
117. Графический метод решения задач линейного программирования.

Графический метод, несмотря на свою очевидность и применимость лишь в случае малой размерности задачи, позволяет понять качественные особенности задачи линейного программирования, характерные для любой размерности пространства переменных и лежащие в основе численных методов ее решения.

Графическое решение этой системы показано на рис. 7.4
Решением этой системы являются координаты всех точек, принадлежащих ОДР, т.е. многоугольнику ABCDO.
Т.к. в ОДР бесчисленное множество точек, значит, рассматриваемая система имеет бесчисленное множество допустимых решений.
Если мы хотим найти оптимальное решение, то мы должны принять целевую функцию. Пусть мы хотим, чтобы решение было оптимальным в смысле максимизации целевой функции F=x₁+x₂→max.

Эта зависимость на рис. 7.5 представлена в форме уравнения прямой с угловым коэффициентом x2=F-x1, из которого видно, что tga= -1. При этом угол a=135°, а величина F равна отрезку, отсекаемому прямой на оси ординат. Если прямую перемещать параллельно самой себе в направлении, указанном стрелками, то величина F будет возрастать. Совместим теперь ОДР, изображенную на рис. 7.4, с линией целевой функции F, построенной на рис. 7.5, получим рис. 7.6.

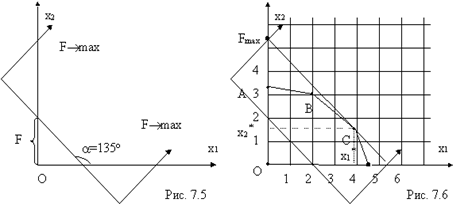
Поскольку требуется найти оптимальное решение, при котором целевая функция F=x1+x2→max, т.е. стремится к максимуму, будем перемещать график целевой функции в направлении увеличения F. Очевидно, что оптимальным решением будут координаты точки С, равные х₁^* и х₂^*. При этом F=F^*.

На основании рассмотренного можно сделать вывод: оптимальным решением являются координаты вершин ОДР.

На этом базируется аналитический метод решения задач линейного программирования, который заключается в следующем:

Похожие работы

Билеты к экзамену по статистике с-х

Скачать

147923

54

14

... предприятия, который определяется: 1 стоимость ВП в текущих ценах за вычетом материальных затрат амортизации. 2. Сумма расходов на оплату труда с отчислениями от прибыли. В органах статистики определяется сумма финансовых потерь с/х пр-ва из-за экономически необоснованных цен.  77. Анализ прироста ВД по факторам. ВД – фактически реализованный ЧП. ВД зависит от массы затрат ...