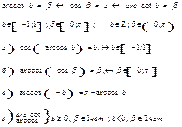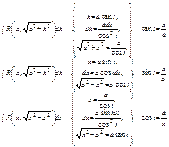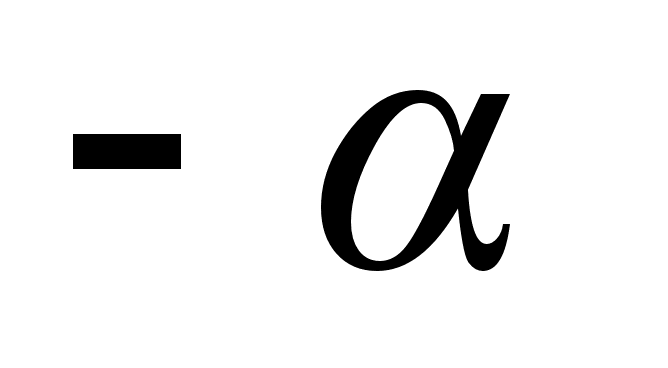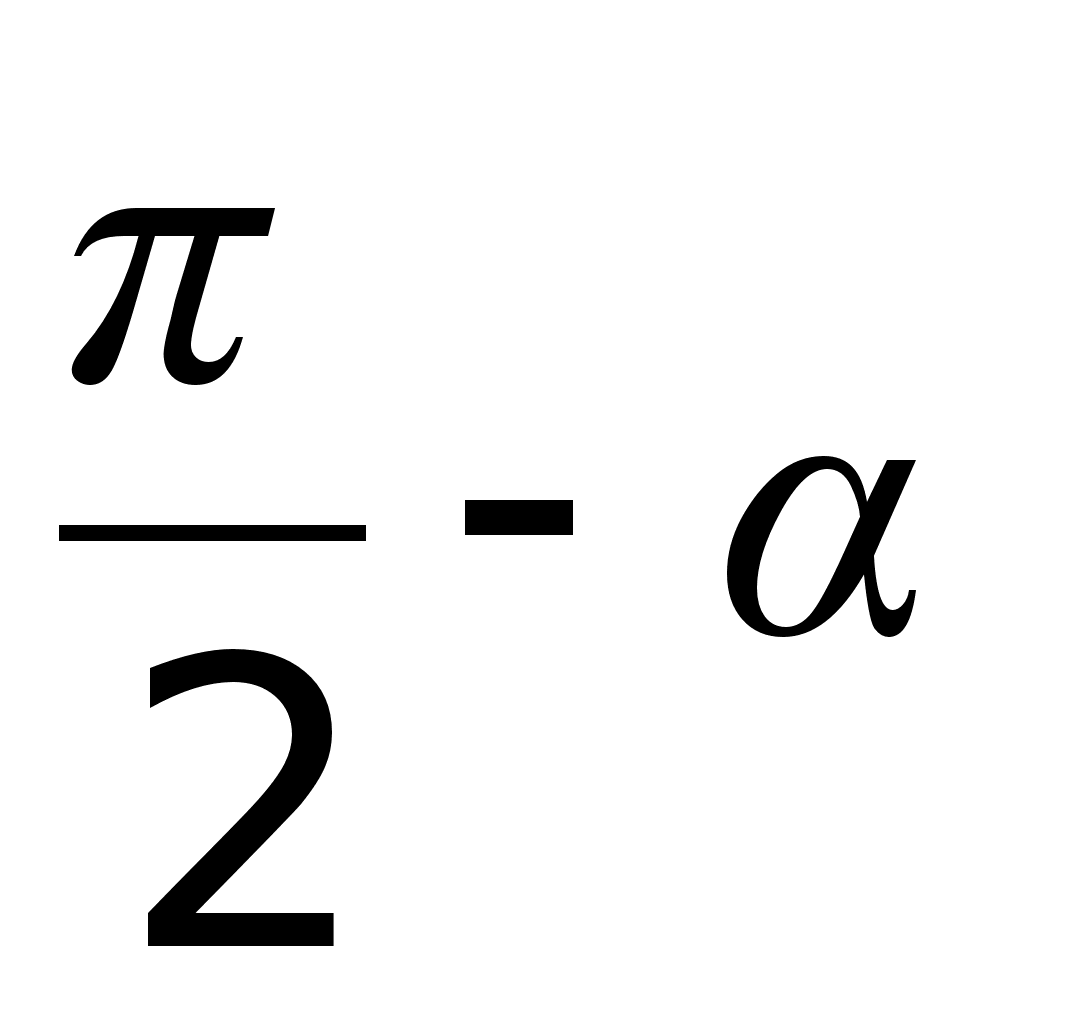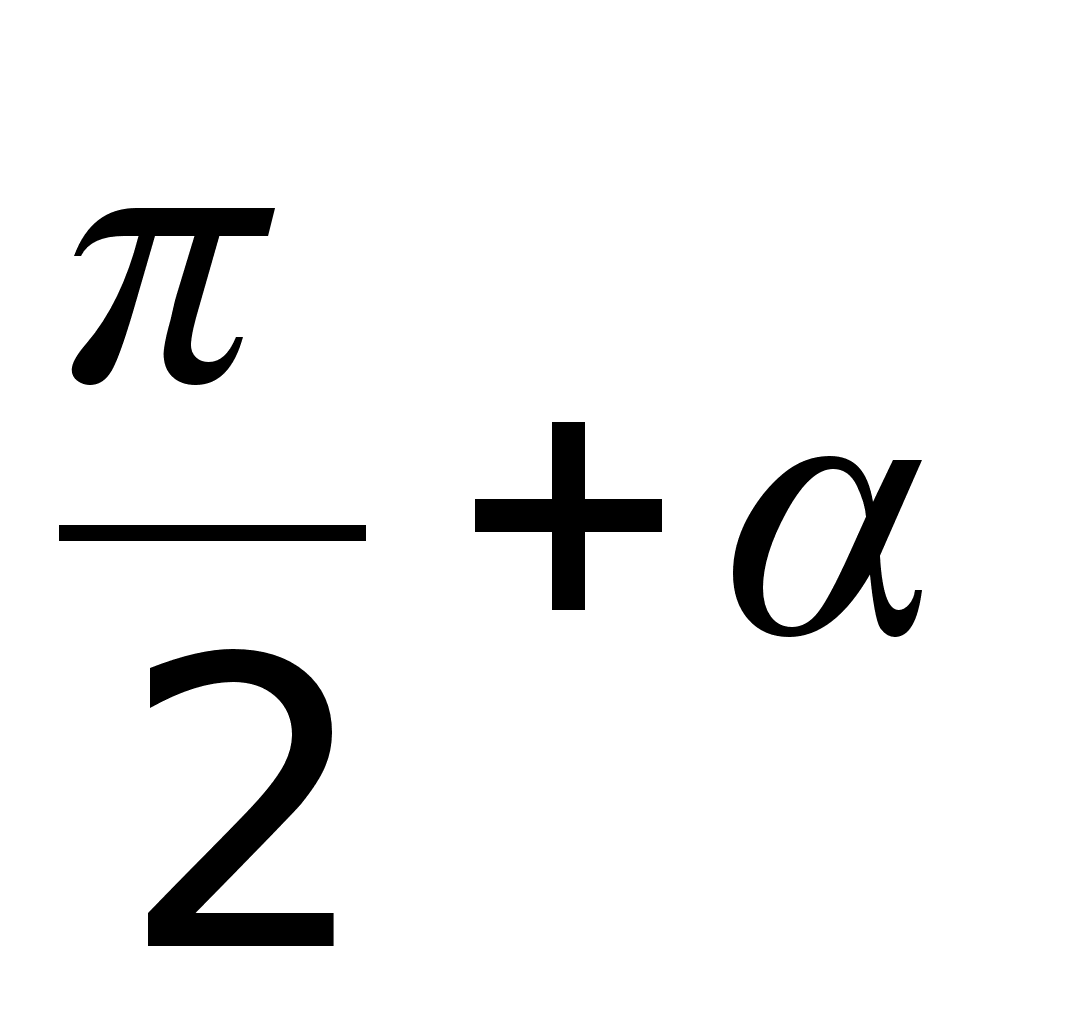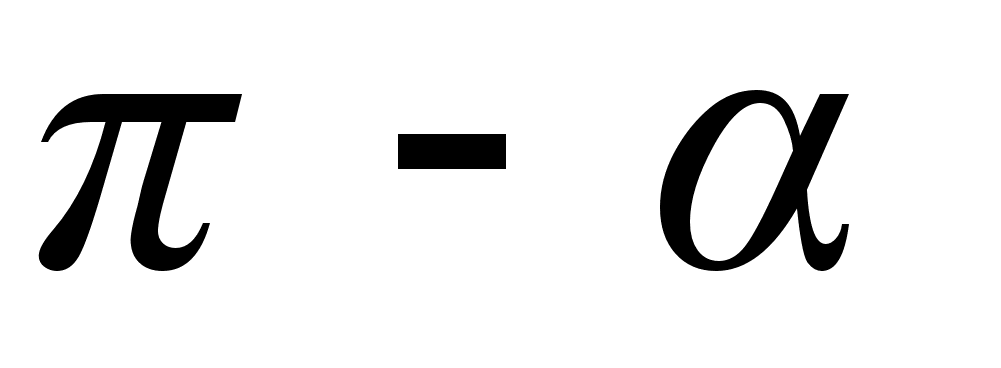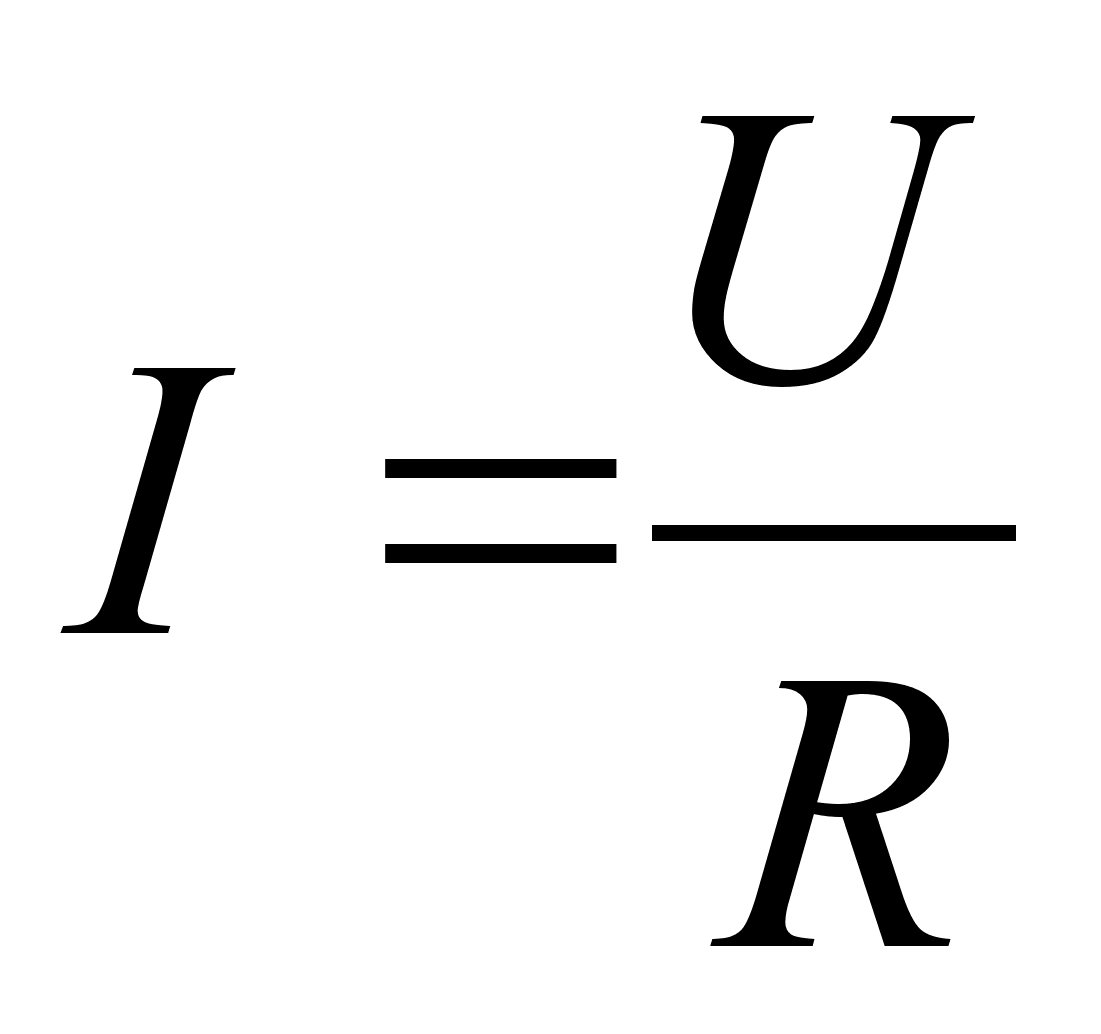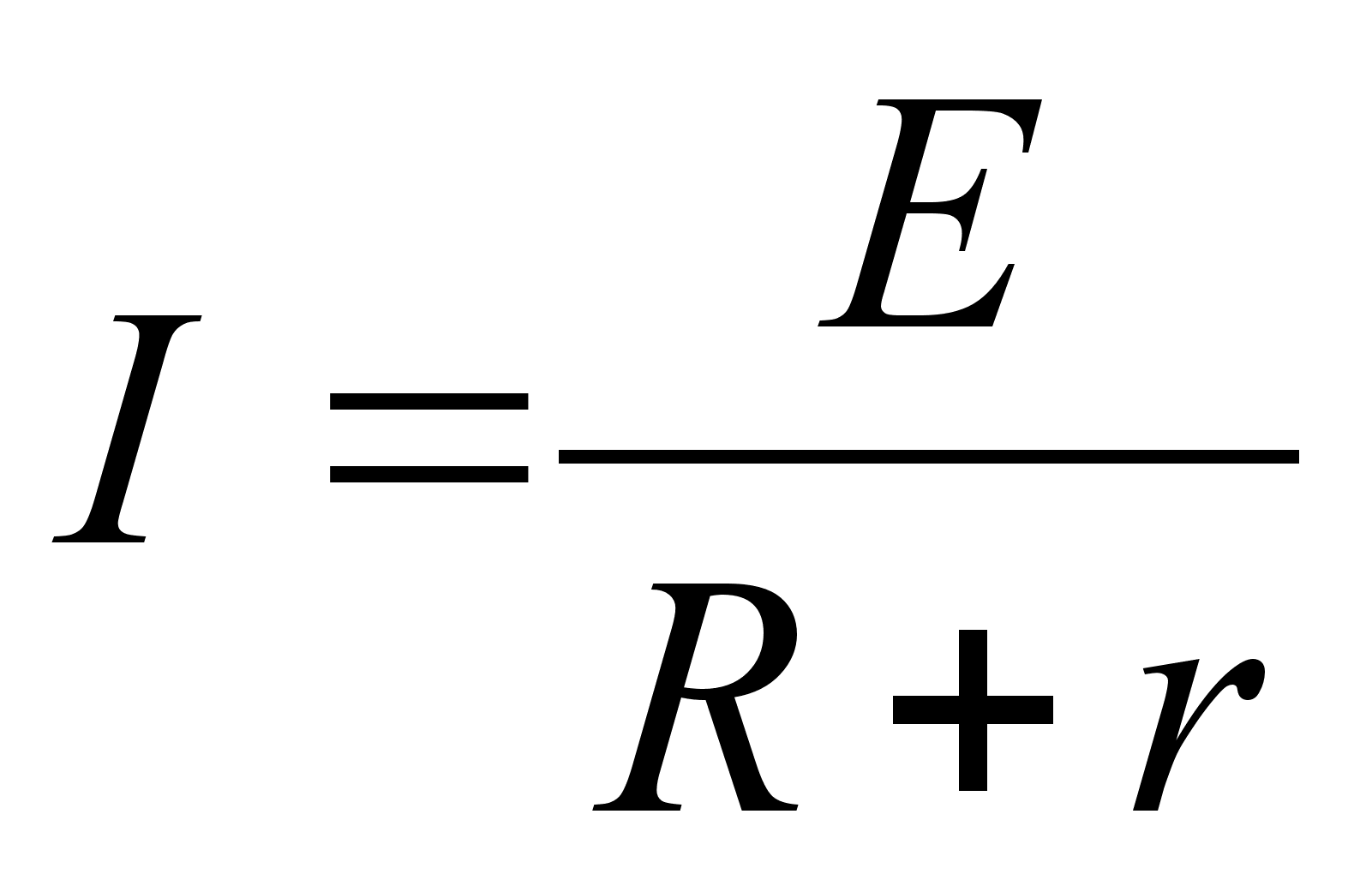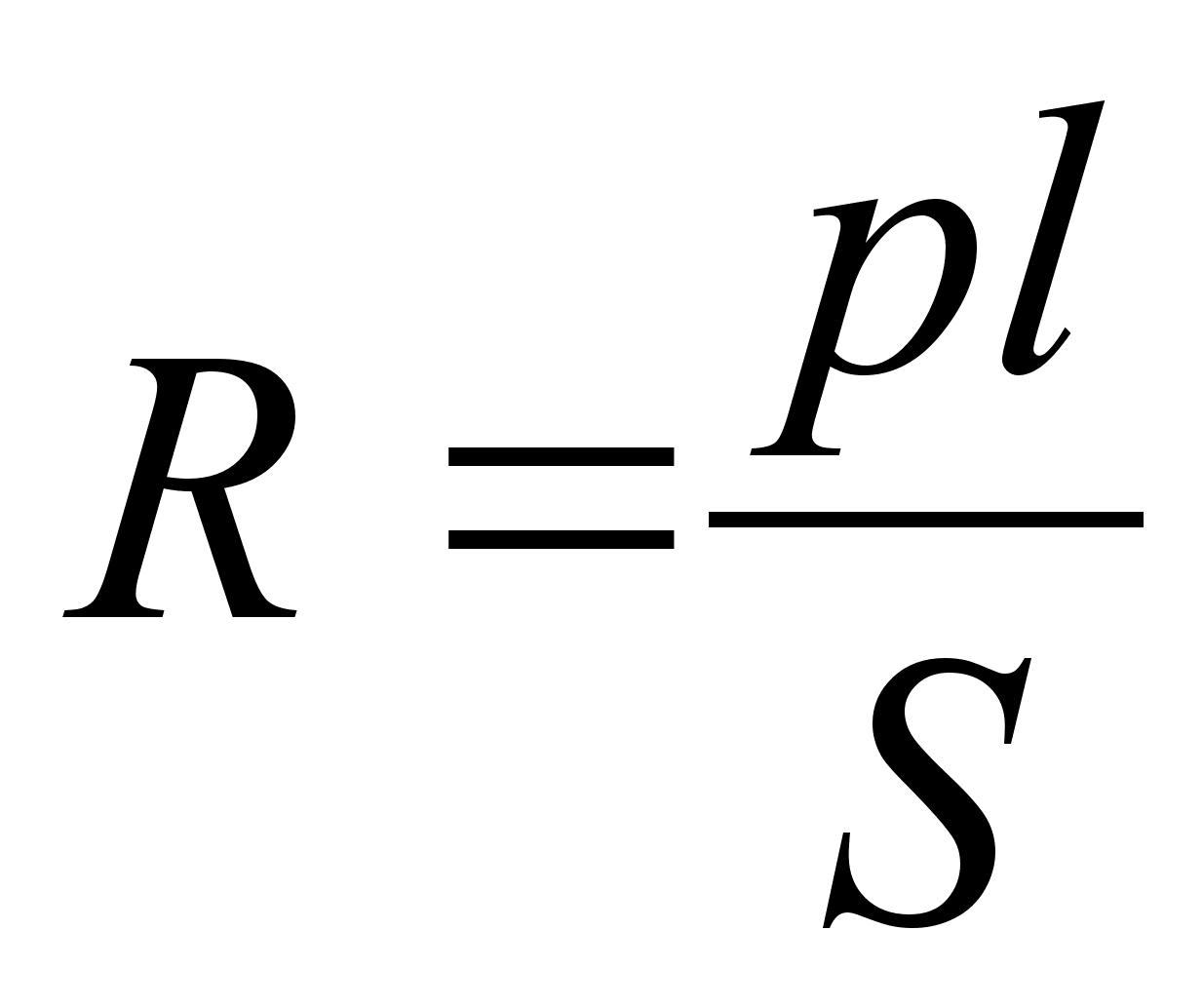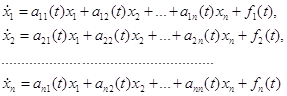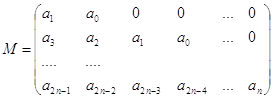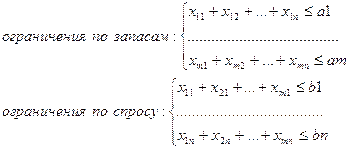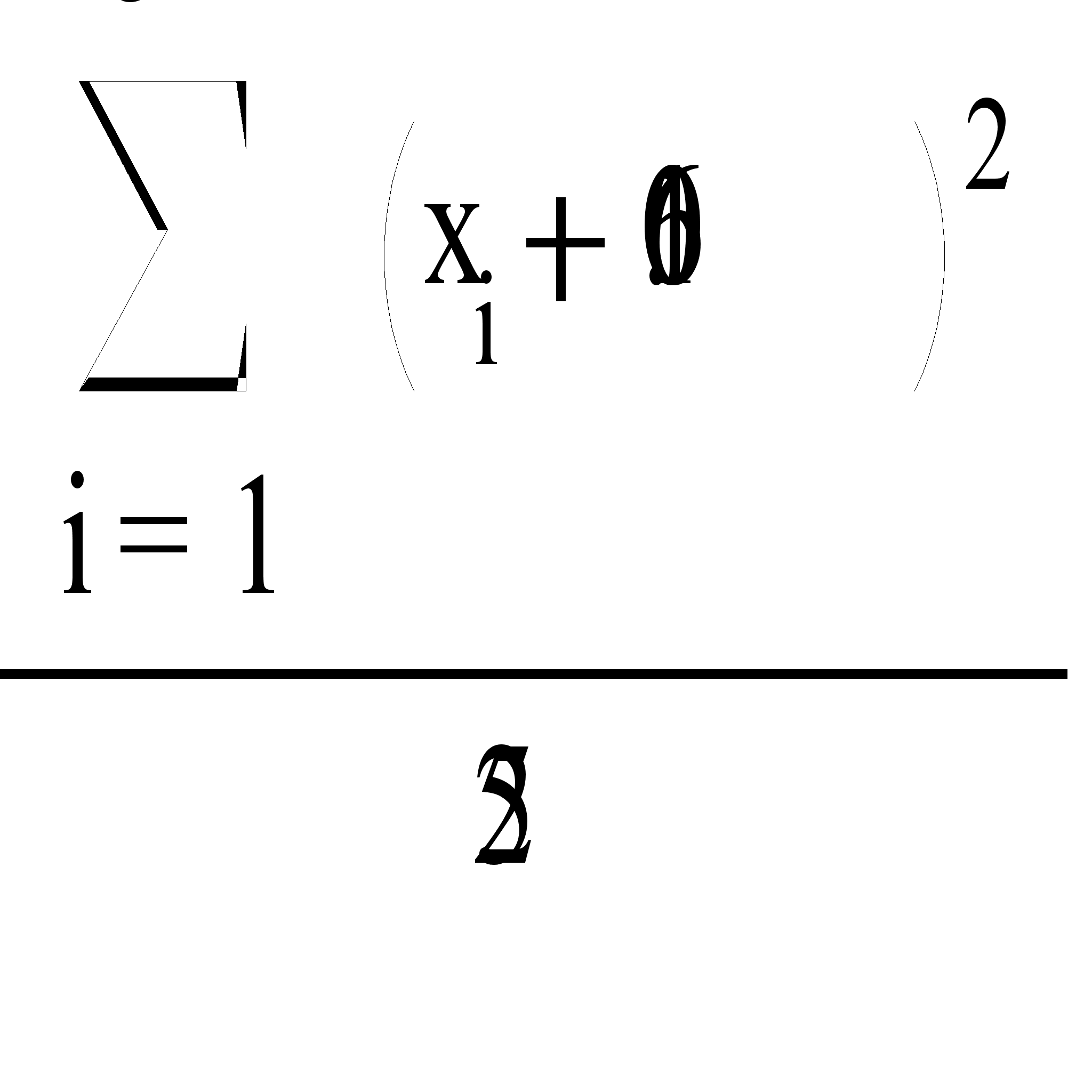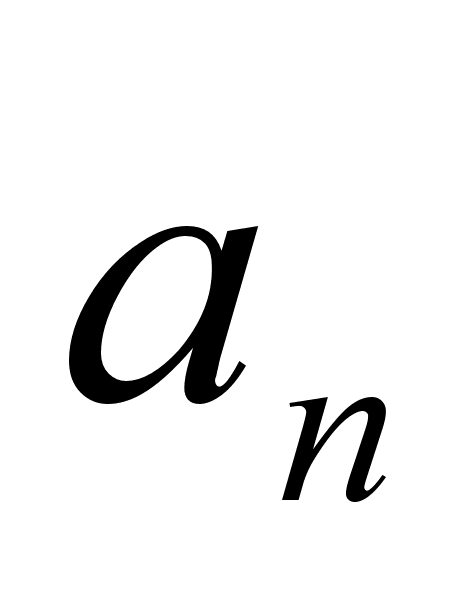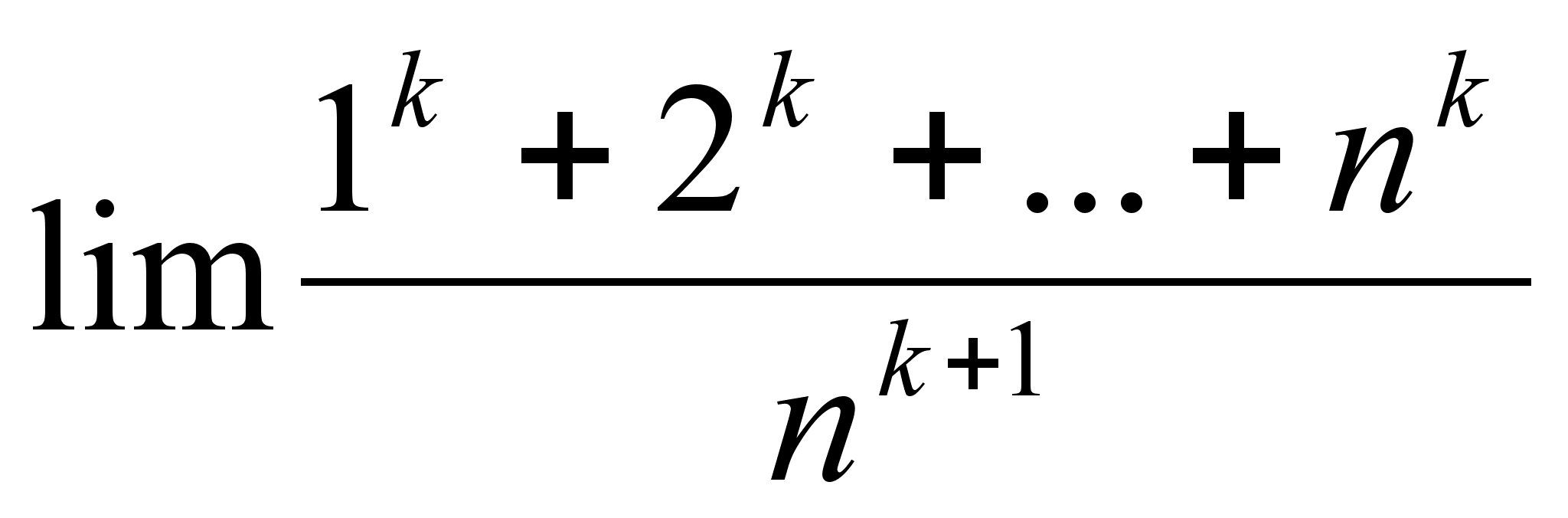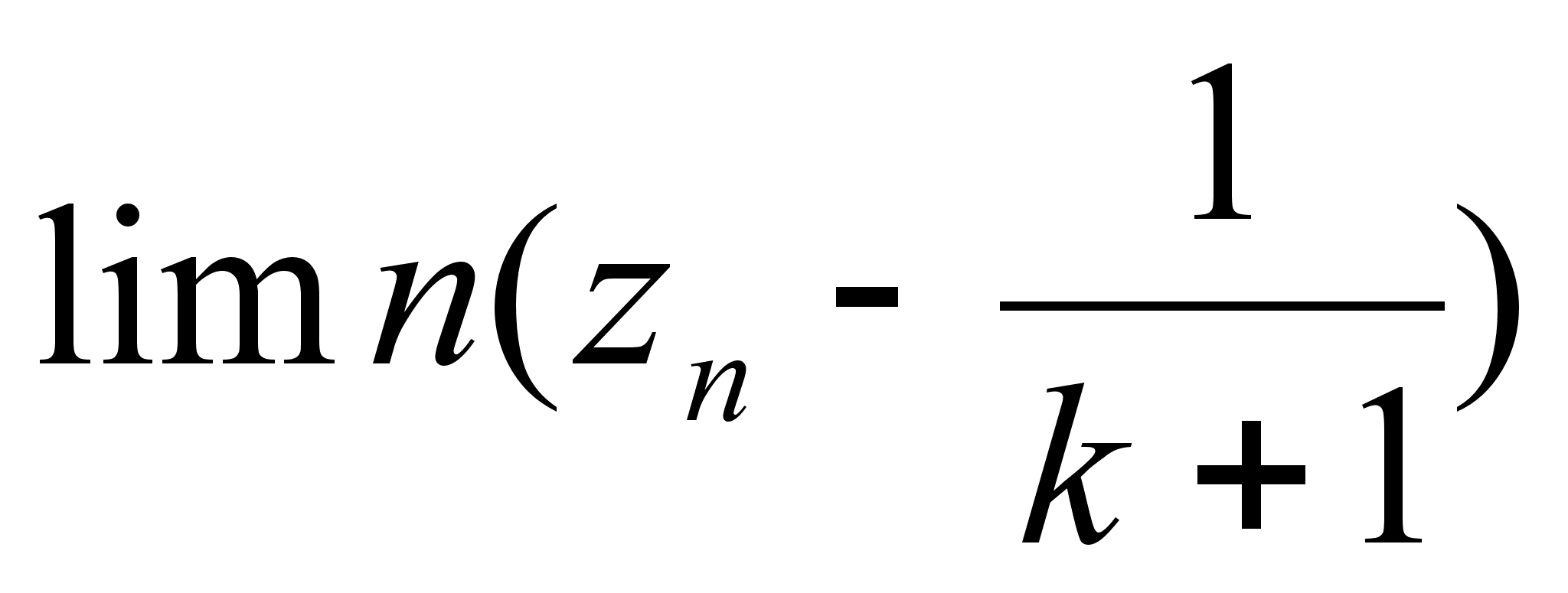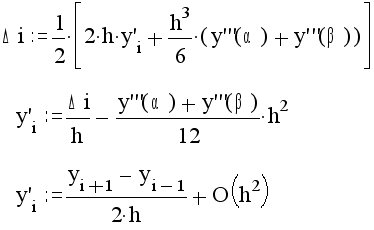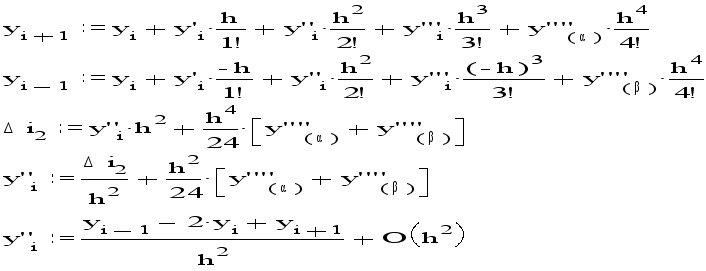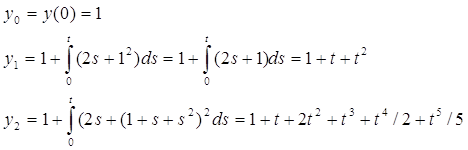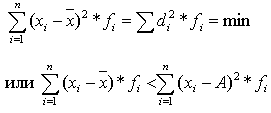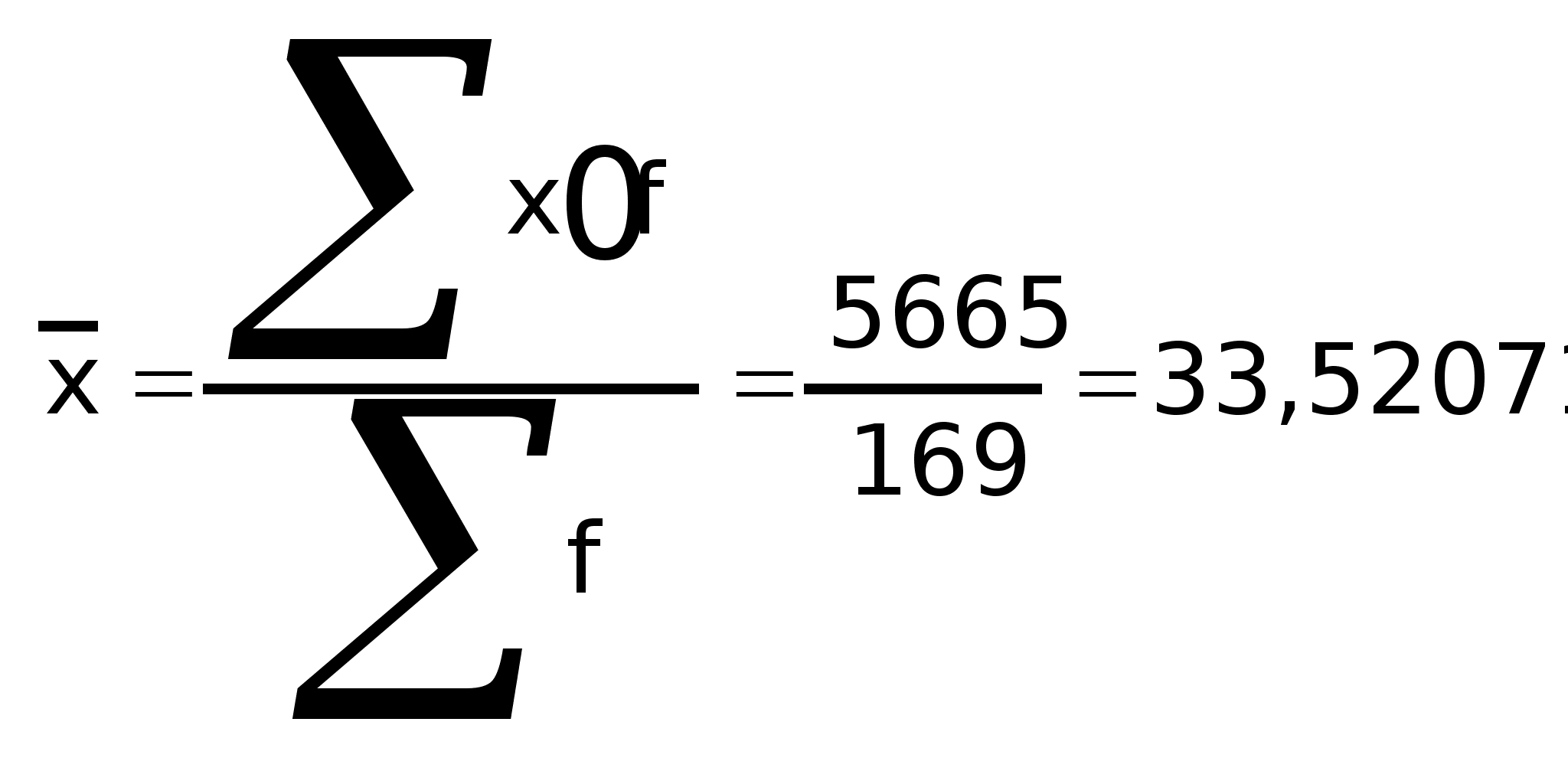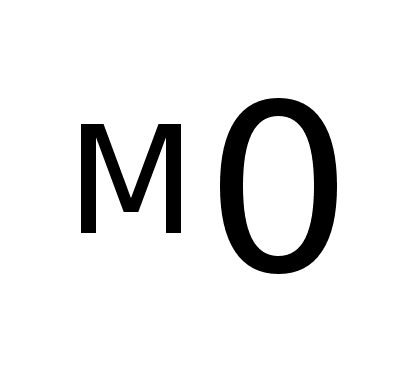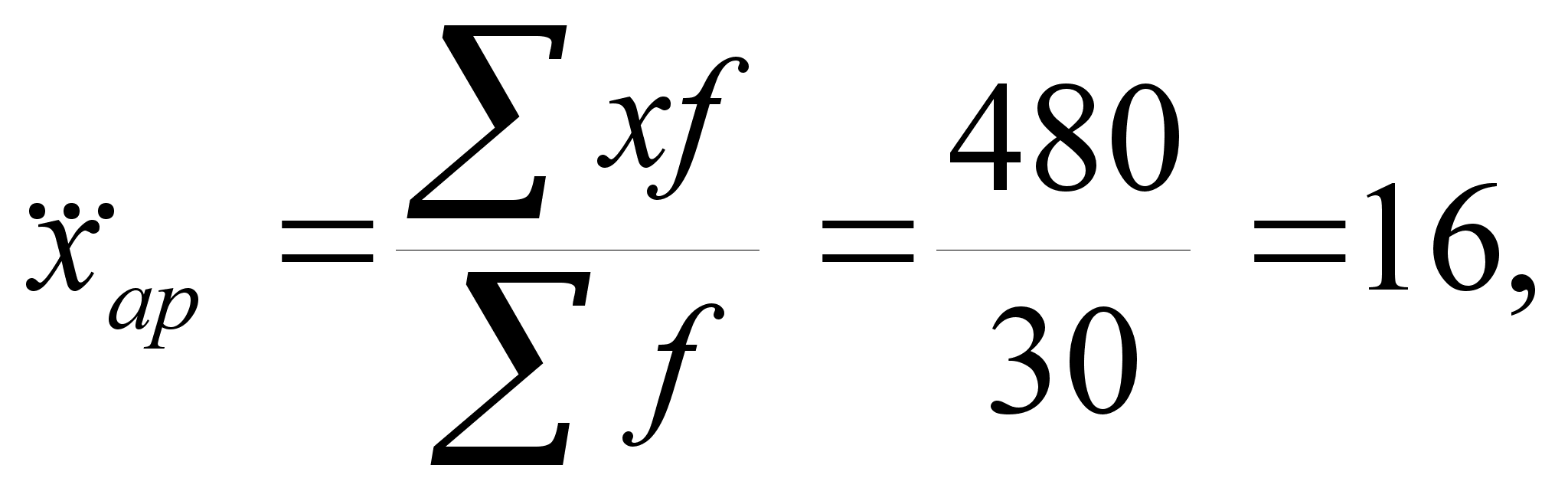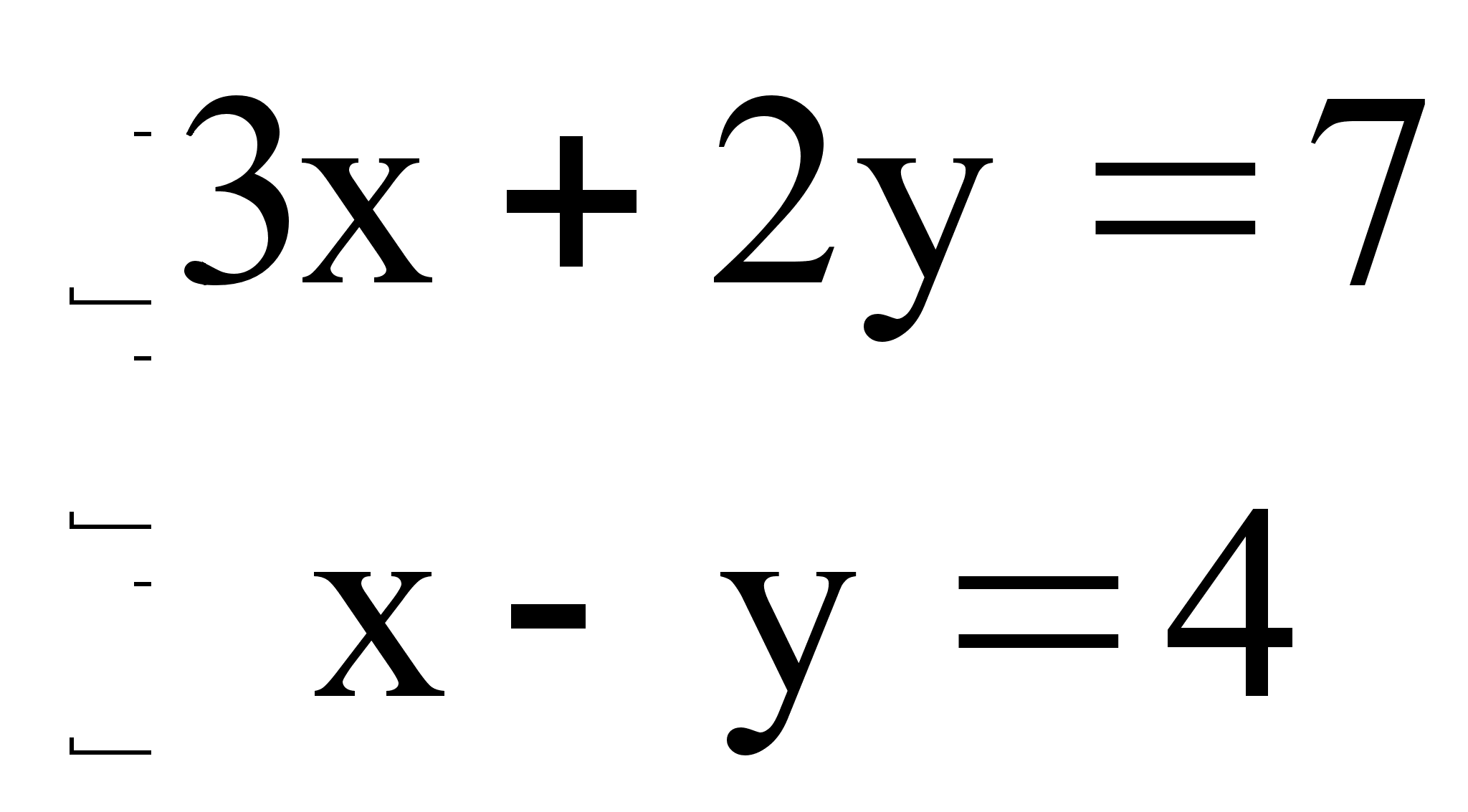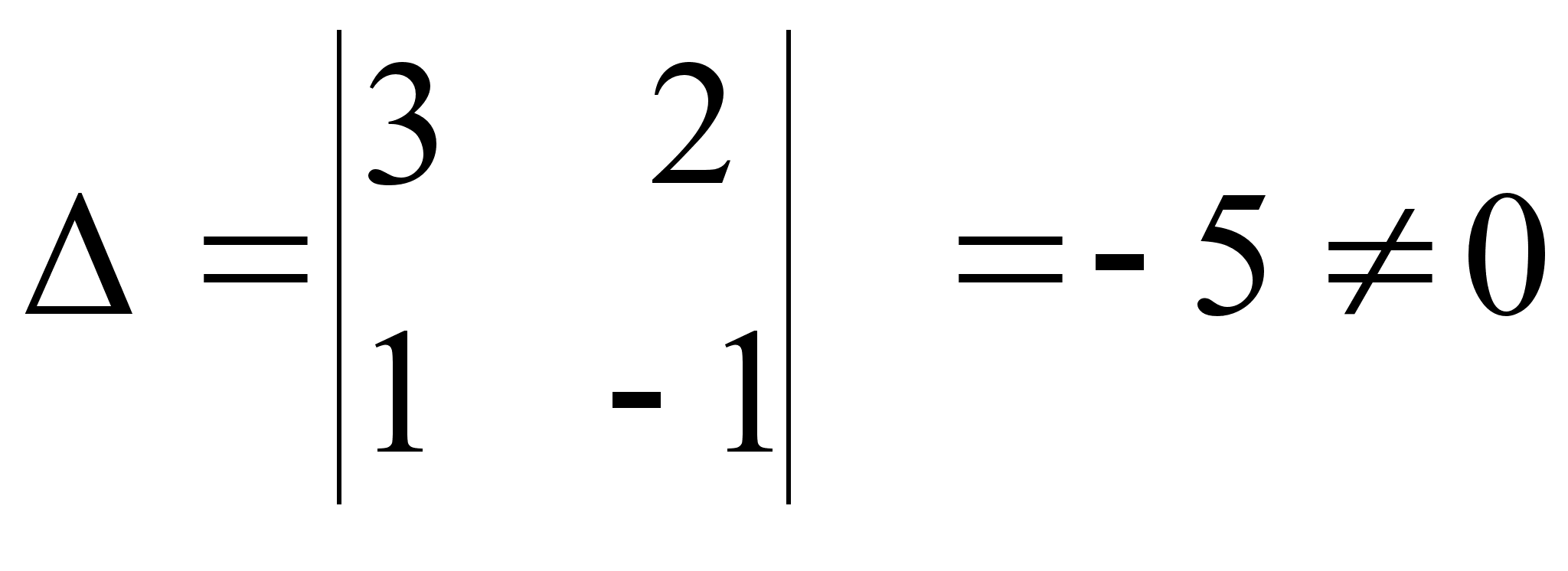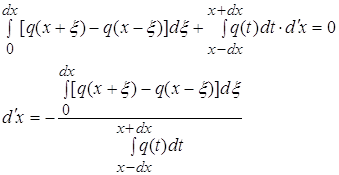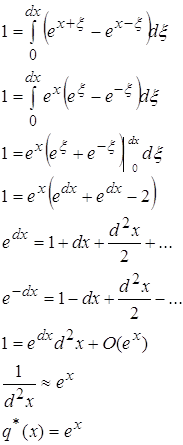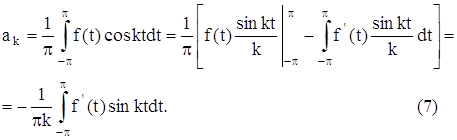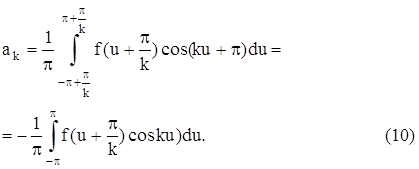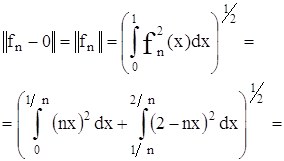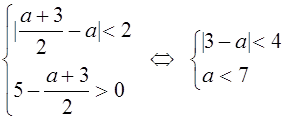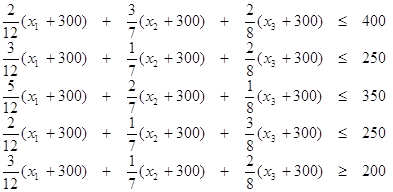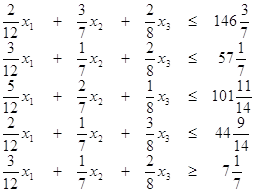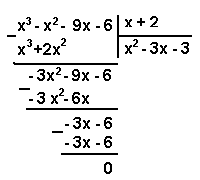| № | Название работы | Скачать |
|---|---|---|
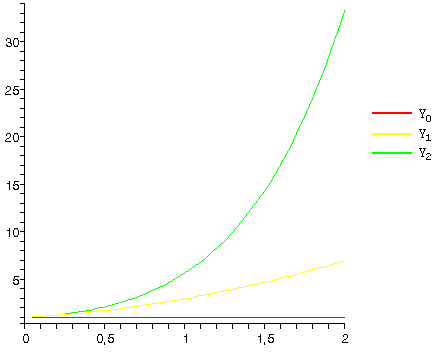
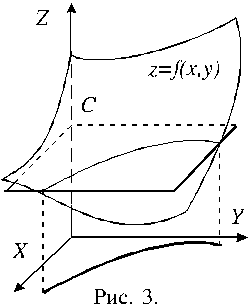
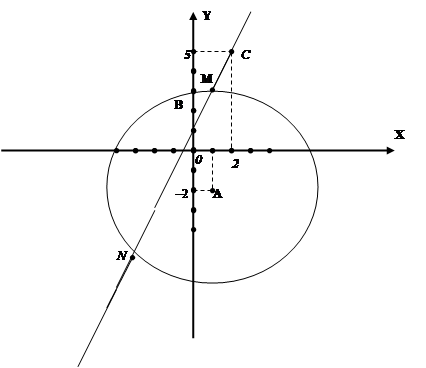
| 2101. |
Функция и ее свойства ... функция с натуральным показателем- функция, заданная формулой y=xn, где n- натуральное число. При n=1 получаем функцию y=x, ее свойства рассмотрены в п.2. При n=2;3 получаем функции y=x2; y=x3. Их свойства рассмотрены выше. Пусть n- произвольное четное число, большее двух: 4,6,8... В этом случае ... |
|
| 2102. |
Формулы тригонометрии sinα+sinβ=2sinЅ(α+β)cosЅ(α-β);
sinα-sinβ=2cosЅ(α+β)sin Ѕ(α-β)
cosα+cosβ=2cosЅ(α+β)cosЅ(α-β);
cosα-cosβ=-2sinЅ(α+β)sin Ѕ(α-β)
a·sinx+b·cosx=(aІ+bІ)sin(x+&beta ... |
|
| 2103. |
Формулы по тригонометрии (шпаргалка) #61537;-tg)/(1+tgtg) ctg(+)=(ctgctg-1)/(ctg+ctg) ctg(-)=(ctgctg+1)/(ctg-ctg) sin2=2sincos=(2tg)/(1+tg2) cos2 ... |
|
| 2104. |
Формулы по математическому анализу ... Если кривая y=f(x) на отрезке [a, b] – гладкая (т.е. производная непрерывна), то длина соответствующей дуги этой кривой находится по формуле При параметрическом задании кривой x=x(t), y=y(t) [x(t) и y(t) – непрерывно дифференцируемые функции] длина дуги кривой, соответствующая ... |
|
| 2105. |
Формулы по математике (11 кл.) ... параллелепипед: Куб: Пирамида: Правильная пирамида: Правильная усечённая пирамида: Цилиндр: Конус: Усечённый конус: 4. Векторы. Равные векторы: Сложение и вычитание: Компланарные векторы: Координаты векторов: Коллинеарные векторы: Некоторые формулы на коо |
|
| 2106. |
Формулы по вышке ... сложения ф-лы понижения степен. Формулы произведения. Ф-лы двойного угла. ЛОГАРИФМ Частн.случ. Ф-ии половинного аргумента ПРАВЕЛА ДИФЕРЕНЦИРОВАНИЯ Ф-лы сокр. ... |
|
| 2107. |
Формулы по алгебре, тригонометрии, электродинамике (Шпаргалка) 61537; 360 – 360 + sin -sin cos cos sin –sin –cos –cos -sin sin &# ... |
|
| 2108. |
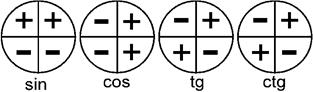
Формулы по алгебре ... a –cos a –sin a sin a cos a cos a tg -tg a ctg a –ctg a –tg a tg a ctg a –ctg a –tg a tg a ctg -ctg a tg a –tg a –ctg a ctg a tg a -tg a -ctg a ctg a Формулы понижения степени Решения тригонометрических уравнений Выражение ... |
|
| 2109. |
Формулы и шпоры 10-11 кл. (информатика, геометрия, тригонометрия ...) (Шпаргалка) -sin(-)) sin sin=1/2(cos(-)-cos(+)) cos(α+β)=cosαcosβ-sinαsinβ sin(α+β)=sinαcosβ+cosαsinβ cos(α -β)=cosαcosβ+sinαsinβ sin(& ... |
|
| 2110. |
Формула Шлетца ...
каноническим.
Таким образом,
в каноническом
репере Якобиева
матрица отображения
f
является единичной
матрицей.
Формулы
(5.7) и (5.8)
в каноническом
репере примут
вид:
x=1+X1+1/2ΛjkXjXk+ (5.9),
y=-1+X2+1/2ΜjkXjXk+ (5.10). §6.
Инвариантная
псевдориманова
метрика. ... |
|
| 2111. |
Формирование понятия цилиндра ... трапеции вокруг оси симметрии. Упражнение 10.Изобразите все возможные сечения усеченного конуса. I этап: Введение понятия сфера и шар. Цель этапа: Формирование понятия сфера (шар) развитие воображения, систематизация знаний по теме вращения. Формирование целостной системы. ... |
|
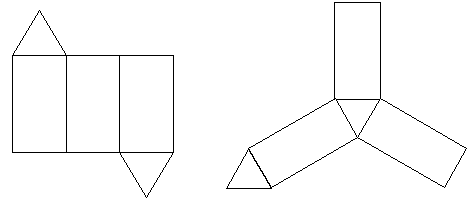
| 2112. |
Формирование понятия призмы и умение ее видеть ... . III этап: Введение понятия развертки призмы (поверхности) Цель: Расширение знаний учащихся связанных с общим понятием призмы. Ввести понятие развертки (опираясь на понятие развертки прямого параллелепипеда на уроках черчения, труда). Оборудование: Картонные модели призм, ножницы, раскладные ... |
|
| 2113. |
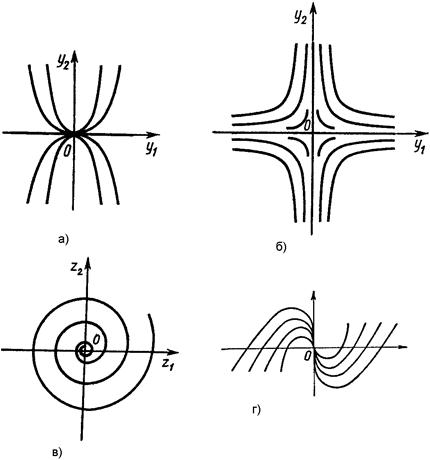
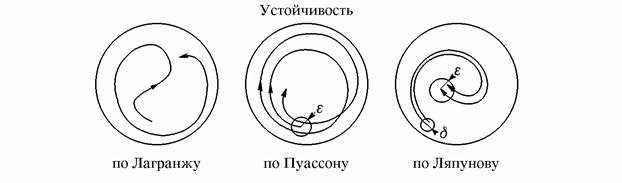
Устойчивость систем дифференциальных уравнений ... уравнение для определения мультипликаторов. Так как , то оно принимает вид , где . 2. Устойчивость решений систем дифференциальных уравнений. 2.1. Устойчивость по Ляпунову. Вводя определение устойчивости по Лагранжу и Пуассону в пункте 1.3, описывались свойства одной отдельно взятой ... |
|
| 2114. |
Уравнения с параметрами ... чего учащиеся решают известным им способом целое уравнение, исключая посторонние корни, т. е. числа, которые обращают общий знаменатель в нуль. В случае уравнений с параметрами эта задача более сложная. Здесь, чтобы исключить посторонние корни, требуется находить значение параметра, обращающее общий ... |
|
| 2115. |
Уравнения математической физики ...
в виде функции
k
переменных;
обозначим
её: µ
§
Необходимое
условие экстремума:
µ
§,
тогда:
µ
§, где i=1,...,k. (1)
Система
алгебраических
уравнений
(1) имеет единственное
решение, т.к.
её определитель
(Грама) отличен
от 0.
µ
§
Обозначим
решение µ
§ , и: µ
§-
монотонно
невозрастающая
... |
|
| 2116. |
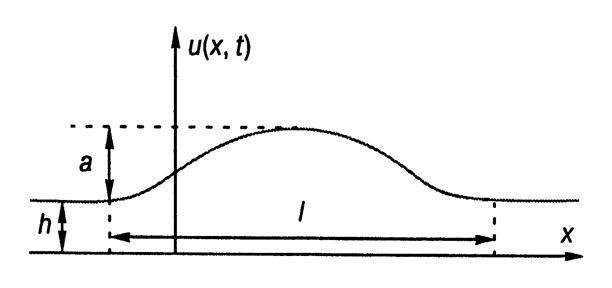
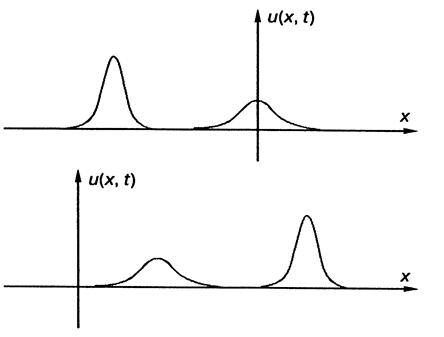
Уравнение Кортевега - де Фриса, солитон, уединенная волна ... , Крускал и Забуски рассмотрели их столкновение. Остановимся подробнее на обсуждении этого замечательного факта. Пусть имеются две уединенные волны, описываемые уравнением Кортевега—де Фриса, которые различаются амплитудами и движутся друг за другом в одном направлении (рис. 2). Из формулы для ... |
|
| 2117. |
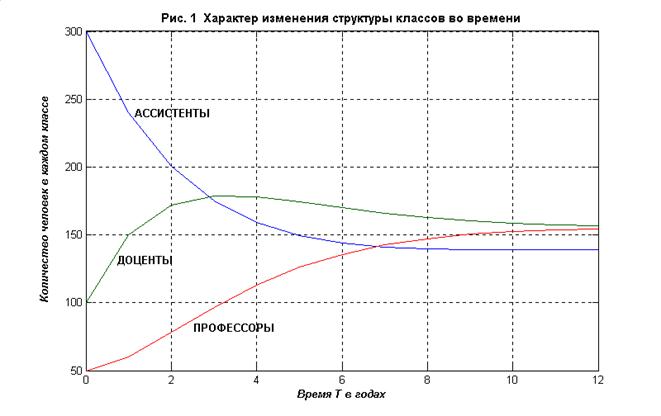
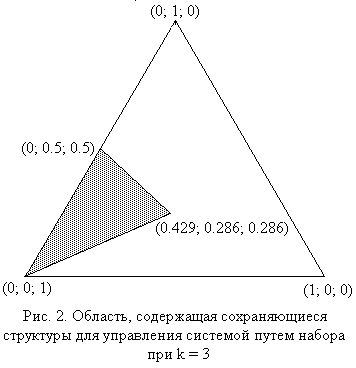
Управление структурой преподавательского состава в университете ... применить эту теорию для ответа на вопросы о поведении модели. 5. Прогнозирование Первый вопрос, который был поставлен относительно структуры преподавательского состава университета, состоял в том, имеется ли тенденция к продолжению роста. На этот вопрос можно ответить, используя запись (6). ... |
|
| 2118. |
Триангуляция quo; 36.64” 86o 39’ 32.25” 146o 03’ 16.98” 233o 01’ 53.80” 295o 38’ 59.70” 0о 00’ 00.00” 31o 17’ 38.08” 86o 39’ 33.40” 146o 03’ 18.18” 233o 01’ ... |
|
| 2119. |
Три кризиса в развитии математики ... на
развитие
современной
математики.
Мы рассмотрим
сущность этих
кризисов
математики,
имея в виду
преимущественно
подтверждение
выводов, сделанных
ранее о закономерностях
развития математики
как теории.
I.
Способы обоснования
математики
в древней Греции
от Пифагора
до Евклида.
1. Математика
... |
|
| 2120. |
Три знаменитые классические задачи древности ... просто накладывает фигуру на фигуру – и только. Задача об удвоении куба Удвоение куба – так называется третья классическая задача древнегреческой математики. Эта задача на ряду с двумя первыми сыграла большую роль в развитии математических методов. Задача состоит в построении куба, имеющий ... |
|
| 2121. |
Транспортная задача ... с не нулевыми перевозками называются базисными, а с нулевыми – свободными. В зависимости от соотношения между запасами и заявками транспортная задача называется сбалансированной или несбалансированной. Сбалансированная ТЗ: Несбалансированная ТЗ: Для сбалансированной ТЗ ограничения принимают вид ... |
|
| 2122. |
Топология как отражение культуры и жизнедеятельности ... истоки понимания культурных процессов как характеристика современной жизни на планете. Массовая коммуникация как процессс распространения информациии в обществе с помощью технических средств. Разнообразие культур, культурных традиций и проблема "понимания". Позвольте в этой статье ... |
|
| 2123. |
Топологические пространства ... и триангулируемости (Дж. Милнор, США). Развитие Т. продолжается во всех направлениях, а сфера её приложений непрерывно расширяется. Определение топологического пространства Напомним классическое определение непрерывности числовой функции f в точке x, восходящее к Коши. Определение 1. Функция f ... |
|
| 2124. |
Тождественные преобразования показательных и логарифмических выражений ... относительно прямой (рис. 3). Рис. 3 Глава 3. Тождественные преобразования показательных и логарифмических выражений на практике. Задание 1. Вычислите: 1.1) ; 1.2) ; 1.3) ; 1.4) ; 1.5) . Решение: 1.1) ; 1.2) ; 1.3) ; 1.4) ; 1.5) . Ответ ... |
|
| 2125. |
Теория флюксий ... находить эти , следующим образом: члены с x3, x2, x, x0 умножаются на 3xx’/x, 2xx’/x, xx’/x, 0/x, а члены с y2, y, y0 на 2yy’/y, yy’/y, 0/y)» § 2. Решение проблем теории флюксий В "Методе флюксий..." (1670-1671) Ньютон формулирует две основные взаимно-обратные задачи анализа: 1)& ... |
|
| 2126. |
Теория устойчивости ... п. 10 ,если
нет специальных
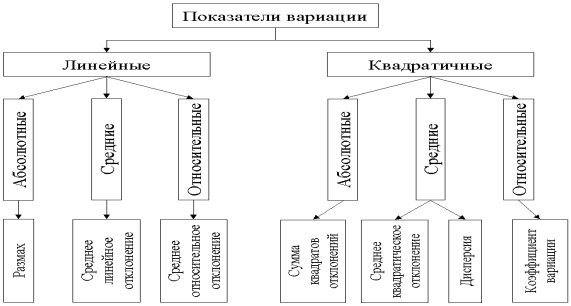
оговорок, приводится
для случая n =
1.
x 0 t Рис.1 Так
как задача
теории устойчивости
впервые возникла
в механике,
то переменную
t принято интерпретировать
как время, а
искомую вектор-функцию x ... |
|
| 2127. |
Теория управления ... : -здесь достигается максимум. 2);
3).
Теорема
о необходимых
условиях
оптимальности.
Если в линейной
задаче быстродействия
мн-ва выпуклы, -оптимальное
управление,
переводящее на
отр. ,
а -соответствующая
траектория,
то пара
удовлетворяет
принципу максимума
Понтрягина.
23.
Применение
необходимых
... |
|
| 2128. |
История статистики ... от начала ряд 95-100 3 3 100-105 20 23 105-110 10 33 110-115 5 38 115-120 4 42 Итого 42 – Модой в статистике называют наиболее часто встречающееся в исследуемой совокупности значение признака. Следовательно, в данной задаче модальным будет интервал ... |
|
| 2129. |
Теория случайных функций ... элемента распределено экспоненциально с параметром . Тип резервироавния - ненагруженный. Для описания состояния системы введем двумерный случайный поцесс (t) = ((t), (t)) с координатами, описывающими: - функционирование элементов (t) {0, 1, 2} - ... |
|
| 2130. |
Теория информации ... А. Реально же, конечно, может получиться и наоборот. Также необходимо заметить, хотя это и не относится к той части теории, которая пригодится нам для решения задач, что информация имеет ярко выраженный материальный характер — то есть она может передаваться только с помощью вещества или энергии. ... |
|
| 2131. |
Теория игр и принятие решений ... которой принимается решение, удовлетворяла свойствам: вероятности появления состояния Fj неизвестны, но некоторые предположения о распределении вероятностей возможны; принятое решение теоретически допускает бесконечно много реализаций; при малых числах реализации допускается некоторый риск. 3о. ... |
|
| 2132. |
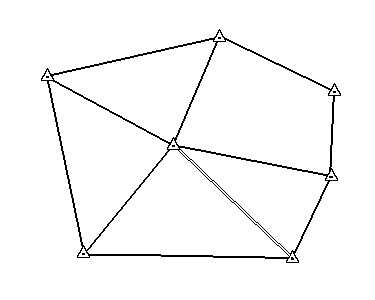
Теория графов ... на рисунке 4.1. На нем выделены три возможных варианта расписания уроков. (РИСУНОК 4.1) Данная задача является классическим примером удачного использования теории графов. В настоящее время существует программа "Расписание 3.0" компьютерной фирмы ЛинTex, в которой она решена с ... |
|
| 2133. |
Теория вероятности и мат статистика ...
события равна
0.
По определению
суммы имеет
место неравенство
W+V=W.
W и V несовместные
события.
По третей аксиоме
теории вероятности
имеем:
P(W+V)=P(Q)=P(U)=1
P(W)+P(V)=P(W)
1+P(V)=1
P(V)=1
Пусть W
состоит из
конечного числа
элементарных
событий W={E1,
E2,..., Em} тогда
по определению
.
... |
|
| 2134. |
Случайное событие и его вероятность ... в виде комбинации некоторых других, более простых событий. Приведём теоремы, с помощью которых можно по вероятностям одних случайных событий вычислять вероятности других случайных событий, каким – либо образом связанных с первыми. Начнём с теорем, которые образуют группу с общим названием «теоремы ... |
|
| 2135. |
Теория вероятностей и случайных процессов ия в
точках 0, 2, 4, 6, 8, 10, 12 и
составляем
матрицу М1. Составим матрицу рабочих значений М1:
0 2 4 6 8 10 12 x1 8 -3,329 -5,229 7,681 -1,164 -6,713 6,751 x2 0 3,637 -3,027 -1,118 3,957 ... |
|
| 2136. |
Теория вероятностей и математическая статистика ... -2.93739249325208 0.163674237751803 -1.9244299300759 -2.50583465100064
Проверим с
помощью критерия
«хи квадрат»
гипотезу о
нормальном
распределении
с нулевым
математическим
ожиданием
отклонений
имеющихся
данных от прямой
регрессии при
уровне значимости
0.05:
Найдем наибольшее
по ... |
|
| 2137. |
Зарождение науки о закономерностях случайных явлении ... выработаны первые понятия и некоторые элементы теории вероятностей. В последующие два века учёные столкнулись с множеством новых задач, связанных с исследованием случайных явлений. Играет ли природа в кости? В середине 19в. преподаватель Высшей реальной школы, в городе Брюнне Грегор Иоганн Мендель ... |
|
| 2138. |
Теория вероятностей ... подсчета вероятности, а классический основан на подсчете числа опытов благоприятствующих данному событию среди всех его возможных исходах. Основы теории вероятности Суммой событий Аi называется событие С состоящее в появлении события А или события В или их обоих вместе. Суммой события А и В ... |
|
| 2139. |
Теория Вероятностей ... и . Действительно, имеем: *=, *=, =, =. Другим примером алгебры событий L является совокупность из четырех событий: . В самом деле: *=,*=,=,. 2.Вероятность. Теория вероятностей изучает случайные события. Это значит, что до определенного момента времени, вообще говоря, нельзя сказать заранее о ... |
|
| 2140. |
Теория вероятностей ... Доказательство. D(x±h)=M((x±h)2)—M2(x±h)=M(x2±2xh+h2)—(M(x)±M(h))2=M(x2)±2M(xh)+M(h2)—+M2(x)+2M(x)*M(h)—M2(h)=D(x)+D(h)±2(M(xh))—M(x)*M(h)=D(x)+D(h)±2mxh Вопрос 31 Мат. статистика опирается на теорию вероятностей, и ее цель – оценить характеристики генеральной совокупности по выборочным данным. ... |
|
| 2141. |
Теория Матриц и Определителей ...
диагоналях
.
Определитель
третьего и
любого другого
порядка находится
примерно также,
а именно: Допустим,
что у нас есть
квадратная матрица
. Определителем
следующей
матрицы является
такое выражение
: a11a22a33
+ a12a23a31 + a13a21a32 – a11a23a32 – a12a21a33 –
a13a22a31..
Как вы
видите он
... |
|
| 2142. |
Теорема сложения вероятностей. Закон равномерной плотности вероятностей ... =0,08. Интересующее нас событие представляет (AUB), поэтому из теоремы сложения вытекает: P(AUB)=P(A)+P(B)=0,20. Таким образом, вероятность какого – либо выигрыша равна 0,2. 3. Закон равномерной плотности вероятности. В некоторых задачах практики встречаются непрерывные случайные ... |
|
| 2143. |
Теорема Штольца ... знаменателю,
применим еще
раз ту же теорему.
Получим
.
Но
,
а ,
так
что, окончательно,
.Пример
1.
===
===
===.
Пример
2.
=
==
==
==
==
==
=.
Пример
3.
=
=.Теорема
Штольца справедлива
для последовательностей,
но т.к. последовательности
есть частный
случай функций,
то эту теорему
можно ... |
|
| 2144. |
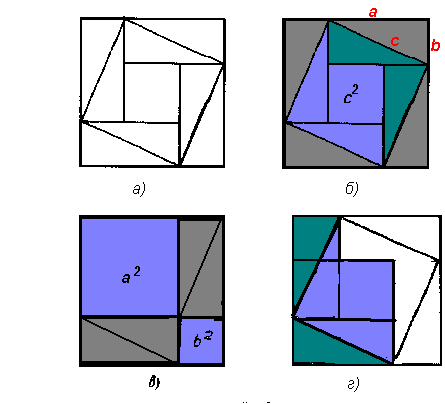
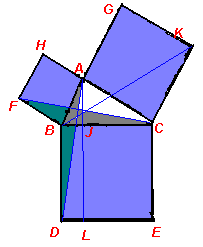
Теорема Пифагора ... называют “креслом невесты”, состоит из двух квадратов со сторонами а и b, т.е. с2=а2+Ь2. На рисунке 3 воспроизведен чертеж из трактата “Чжоу-би...”. Здесь теорема Пифагора рассмотрена для египетского треугольника с катетами 3, 4 и гипотенузой 5 единиц измерения. Квадрат на гипотенузе содержит 25 ... |
|
| 2145. |
Теорема Безу ... натуральных степеней на сумму их оснований не делится . Пусть P(x) = x2k+1 - a2k+1 – разность одинаковых нечётных степеней . По теореме Безу
при делении x2k+1 - a2k+1 на x + a = x – (-a) остаток равен
R = P(-a) = (-a)2k+1 – a2k+1 = -2a2k+1 Т. к. остаток при ... |
|
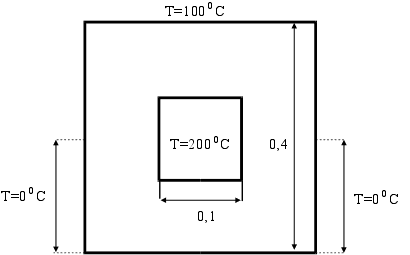
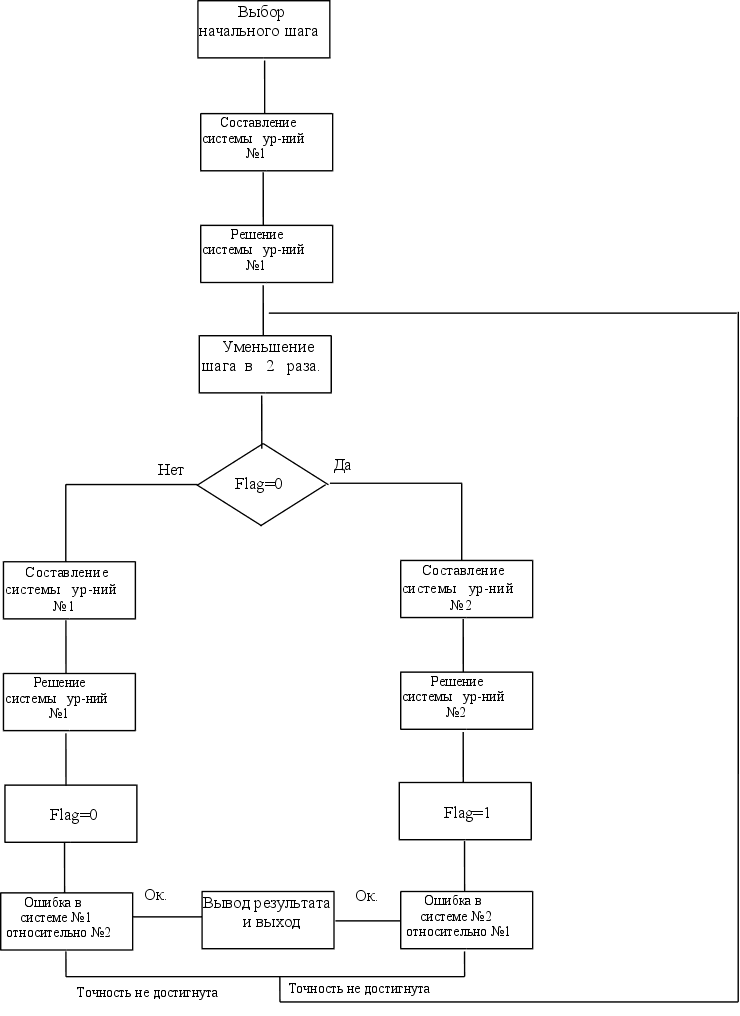
| 2146. |
Температурный расчет с помощью вычислений информационной математики ... тех пор, пока
действительная
погрешность
корней не станет
меньше заданной.
Различные
методы отличаются
друг от друга
способом вычисления
очередного
приближения,
но во всех методах
существуют
две главные
проблемы:
обеспечение
сходимости
процесса итераций;
оценка
достигнутой
погрешности.
... |
|
| 2147. |
Тела вращения ... диаметром. Концы любого диаметра называются диаметрально противоположными точками шара. Шар, так же как цилиндр и конус, является телом вращения. Он получается при вращении полукруга вокруг его диаметра как оси. Пирамида Пирамидой называется многогранник, который состоит из плоского ... |
|
| 2148. |
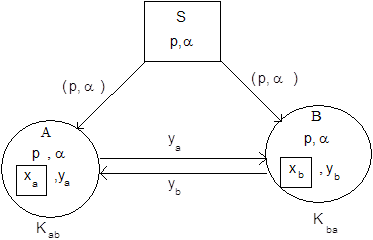
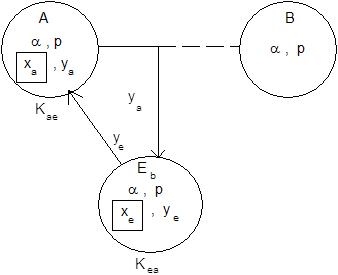
ТИПИЧНЫЕ ДЕФЕКТЫ В КРИПТОГРАФИЧЕСКИХ ПРОТОКОЛАХ ... аутентифицированного ключевого обмена, который завершается формированием общего сеансового ключа. Дефекты в криптографических протоколах В последующих разделах рассматриваются протоколы с типичными дефектами. Примеры протоколов разбиты на группы по типу используемой криптосистемы: - & ... |
|
| 2149. |
Счётные множества ... , мы перенумеруем множество Y, причём в силу бесконечности его, нам придется на эту нумерацию израсходовать все натуральные числа. Следовательно, множество Y является счётным множеством. Приведем пример непосредственно относящийся к этой теореме. Пример: Множество Х={1, ,} как известно, является ... |
|
| 2150. |
Существование решения дифференциального уравнения и последовательные приближения ... как последовательность сходится, то последовательность приближений является равномерно сходящийся на этом отрезке. Список использованной литературы 1. Л.С. Понтрягин. «Обыкновенные дифференциальные уравнения», М.: Государственное ... |
|
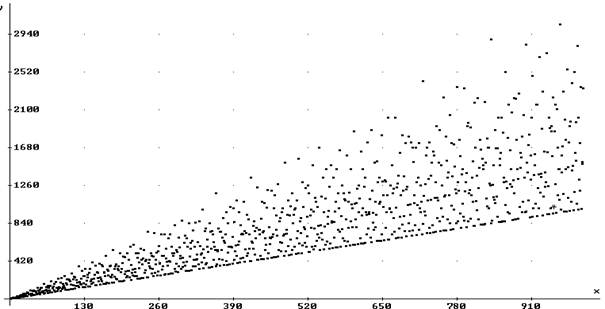
| 2151. |
Сумма делителей числа ... по его сумме делителей не всегда возможно и не всегда однозначно. Теперь построим график. По оси Х расположим числа, а по оси Y их сумму делителей (числа от 1 до 1000): Посмотрим, что же у нас получилось: на графике отчётливо просматриваются несколько прямых линий, например, ... |
|
| 2152. |
Структура сходящихся последовательностей ... Элементы последовательности {yn-xn} неотрицательны, а поэтому неотрицателен и ее предел . Отсюда следует, что . Следствие 2: Если все элементы сходящейся последовательности {xn} находятся на сегменте [a,b], то и ее предел с также находится на этом сегменте. Это выполняется, так как а& ... |
|
| 2153. |
Структура аффинного пространства над телом ... из теоремы 8.1 и опираясь на характеризацию аффинных многообразий, представленную теоремой 4.8, мы докажем здесь следующую теорему: Теорема 9.1. Пусть ,аффинные пространства над телами , , отличными от поля ; для того, чтобы отображение было полуаффинным, достаточно, чтобы 1). Образ любой прямой ... |
|
| 2154. |
Статистические величины ... средней арифметической потеряли свою актуальность в связи с использованием ЭВМ при расчете обобщающих статистических показателей. Абсолютные и относительные статистические величины. Результаты статистического наблюдения регистрируются в виде первичных абсолютных величин. Абсолютная ... |
|
| 2155. |
Статистика (шпаргалка 2002г.) ... цен Пааше является
средней гармонической
величиной из
индивидуальных
индексов, взвешенных
по стоимости
текущего периода. 7вопрос
Относительные
величины
Статистика
широко применяет
относительные
величины, потребность
в которых возникает
на стадии обобщения.
Они помогают
установить
закономерности,
в ... |
|
| 2156. |
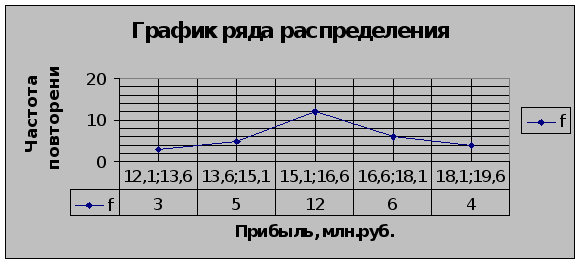
Статистика ... 8.1225 32.49 Итого: 30 - 480 - - 87.075
Дисперсия
имеет большое
значение в
экономическом
анализе. В
математической
статистике
важную роль
для характеристики
качества
статистических
оценок играет
их дисперсия.
Среднее
квадратическое
... |
|
| 2157. |
Статистика ставить
ряд на графике,
отметить на
нем средние
величины и
сделать выводы
о характере
распределения. Построить кореляционное поле связи между (Yi) и (Xi). Сделать предварительный вывод о характере связи. Определить параметры уравнения парной регрессии и коэффициент кореляции. Определить параметры ... |
|
| 2158. |
Статистика Для заполнения таблицы №2 на основании данных из таблицы №1, нижнюю границу первого интервала принимаем равной минимальному значению факторного признака, а верхнюю границу каждого интервала получаем прибавлением к нижней границе величины интервала: Таблица №2 № п/п ... |
|
| 2159. |
Сравнительный анализ алгоритмов построения выпуклой оболочки на плоскости ...
следует теорема:
Теорема 7.
Выпуклая
оболочка множества
из N точек на
плоскости может
быть найдена
с помощью открытого
алгоритма за
время (N
log N)
и со временем
коррекции (log
N).Сравнительный
анализ алгоритмов
построения
выпуклой оболочки
Так как теоретически
показали, что
время ... |
|
| 2160. |
Справочник по геометрии (7-9 класс) ... -ка,
то такие
ны
стороне и 2
прилежащим
к треуг-ки
равны.
ней
углам другого
треуг-ка, то
такие
треуг-ки равны. Определение:
Окружность
называется
геометр-ая
фигура, состоя-щая
из всех точек,
располож-ых
на заданном
расс-нии от
данной точки.
Глава
I I I.
Параллельные
прямые.Определение:
Две ... |
|
| 2161. |
Способы решения систем линейных уравнений ... учащимися,
так и преподавателями
в процессе
факультативных
занятий, как
пособие для
самостоятельного
изучения по
теме „Способы
решения систем
линейных уравнений
”, а также в качестве
дополнительного
материала.
МОУ
Гимназия № 11Способы
решения систем
линейных уравнений
Анжеро-Судженск
... |
|
| 2162. |
Софья Ковалевская ... приходилось
самому приниматься
за решение
разных проблем,
чтобы достойно
ответить на
сложные вопросы
ученицы. "Мы
должны быть
благодарны
Софье Ковалевской,
- говорили
современники,
- за то, что она
вывела Вейерштрасса
из состояния
замкнутости".
Она
изучала новейшие
математические
труды ... |
|
| 2163. |
Составление и решение нестандартных уравнений графоаналитическим методом ... сложным и утомительным преобразованиям. Процесс может быть тогда упрощен и, если применять так называемый графоаналитический метод. ЦЕЛЬ: научиться составлять и решать нестандартные уравнения, которые содержат элементарные функции, проходимые по школьной программе, с использованием ... |
|
| 2164. |
Современные криптографические методы ...
в 2030 г.
Других
способов повышения
вычислительной
мощности нет.
Таким образом,
с точки зрения
защиты информации
криптографическими
методами, анализ
потенциальных
возможностей
метода распределенных
вычислений
представляет
как для криптоаналитиков,
так и для разработчиков
криптографических
систем ... |
|
| 2165. |
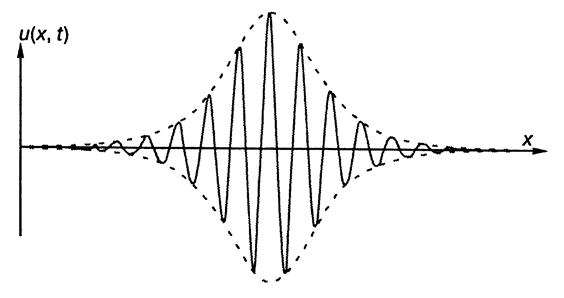
Случайные функции ... сдвигом t = t1—t. Спектральная плотность стационарных процессов Рассмотрим так называемую энергетическую форму интеграла Фурье. Если рассматривается некоторая случайная функция времени х {t), то для нее эти формулы могут быть записаны в виде Возьмем квадрат модуля изображения Фурье [ F (iw)) ... |
|
| 2166. |
Сложения и вычитания чисел с плавающей запятой ... 7] = 1001110;
РгСм
[0] :== если
Тг3н1=0 то 0;
ШИВых:
= РгСм = 0 1001101
110100111000110000010101 = 0
4D D38C15;
КОНЕЦ.
Сложения
и вычитания
чисел с плавающей
запятой
1.
Производится
выравнивание
порядков чисел.
Порядок меньшею
(по модулю) числа
принимается
равным порядку
большего числа,
а мантисса
... |
|
| 2167. |
Система Лотка-Вольтерра ... P не сущ. исток седло седло Q не сущ. не сущ. исток неуст. фокус 4.1 Параметрические области системы 4.2 Область 1: 4.3 Область 2: 4.3 Область 3’ : 4.5 Область 3 – ... |
|
| 2168. |
Синтез оптимальных уравнений ... находится в данный момент фазовая точка. Функцию v(x), дающую уравнение оптимальных траекторий в форме (1.35), называют синтезирующей функцией, а задачу нахождения синтезирующей функции ─ задачей синтеза оптимальных управлений. В разобранном примере синтезирующая функция была кусочно- ... |
|
| 2169. |
Синтез САУ ... D – разбиения
в области заданного параметра
( k ). Построение ЛАЧХ в соответствии с заданным перерегулированием, временем нарастания
и временем
переходного
процесса. Синтез
САУ Все
математические
задачи, решаемые
в ТАУ, делятся
на два класса:
задача
анализа и задача
синтеза.
В задачах ... |
|
| 2170. |
Симметрия ... — левой. Пуговицы на куртке и на рубашке сидят ровно посередине, а если и отступают от нее, то на симметричные расстояния. Но на фоне этой общей симметрии в мелких деталях мы умышленно допускаем асимметрию, например расчесывая волосы на косой пробор — слева или справа. Или, скажем, помещая на ... |
|
| 2171. |
Сетевые методы в планировании ... нашла
свое применение в решении целого
ряда экономических
задач. Эту область
приложения
теории графов
можно назвать:
“Календарное
планирование
программ сетевыми
методами”.
Изучение именно
этой области
является основной
целью моего
курсового
проекта.
Программа
определяет
совокупность
... |
|
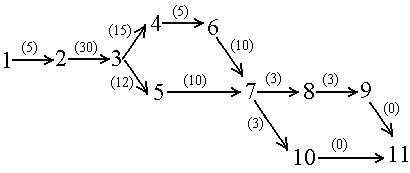
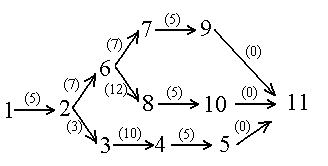
| 2172. |
Сетевые графики ... срок завершения всего проекта в целом. Приведем запись алгоритма, непосредственно вычисляющего характеристики РНАЧ и РВЫП. АЛГОРИТМ 1. Данные: Сетевой график G работ V, заданный списками ПРЕДШ(v), vÎV. Результаты: Наиболее ранние возможные сроки начала и выполнения работ РНАЧ(v), ... |
|
| 2173. |
Середні Значення ... влучень. Для першого учня: Для другого учня: Отже, в команду слід узяти другого учня. Розглянемо деякі властивості середнього арифметичного. 1) Знайдемо відхилення l кожного значення xj від середнього. Різниця х —може бути від'ємною або додатною. Сума всіх п відхилень дорівнює нулю. ... |
|
| 2174. |
Свойства усредненной функции с сильной осцилляцией ... при Введем в рассмотрение функцию с помощью следующего равенства: (1) Назовем эту функцию усреднением функции Это название оправдано так как из (1) и теоремы о среднем для интегралов можем заключить § 2 Свойства функции . 1. Если , при , то при ... |
|
| 2175. |
Сборник Лекций по матану ной
§1. Основные
понятия
Пусть
D
—
некоторое
множество
чисел. Если
задан закон,
по которому
каждому числу
x
из множества
D
ставится в
соответствие
единственное
определенное
число
y,
то будем говорить,
что на множестве
D
задана функция,
которую назовём
f.
Число y
— это значение
функции f
в
точке ... |
|
| 2176. |
Сборник Лекций 2 по Мат.Анализу ,...,
xn).
Переменные
x1,
x2,
..., xn
являются аргументами
этой функции,
а переменная
y функцией
от n переменных.
Далее
будем говорить
лишь о функции
двух переменных.
Для функций
большего числа
переменных
все факты,
о которых будет
идти речь,
или аналогичны
или сохраняются
без всякого
изменения. ... |
|
| 2177. |
Определенный интеграл ... неопределенным интегралом. Это понятие выделил Лейбниц, который заметил, что все первообразные функции отличаются на произвольную постоянную. А называют определенным интегралом (обозначение ввел К. Фурье (1768-1830), но пределы интегрирования указывал уже Эйлер). Самое важное из истории ... |
|
| 2178. |
СИНГУЛЯРНОЕ РАЗЛОЖЕНИЕ В ЛИНЕЙНОЙ ЗАДАЧЕ МЕТОДА НАИМЕНЬШИХ КВАДРАТОВ ... m, но от m зависит работа, затрачиваемая на выполнение каждого преобразования. глава 3. Использование сингулярного разложения в методе наименьших квадратов При использовании метода сингулярного разложения (SVD – Singular Value Decomposition) мы проводим разложение для матрицы плана. При этом ... |
|
| 2179. |
Ряды Фурье и их приложения ... рядами Фурье, довольно широк. Поэтому ряды Фурье нашли широкое применение в различных отделах математики. Особенно успешно ряды Фурье применяются в математической физике и её приложениях к конкретным задачам механики и физики. Этот вопрос можно решить с помощью теоремы Дирихле. («Краткий курс ... |
|
| 2180. |
Ряды ... : Если члены знакочередующегося ряда убывают по абсолютной величине U1>U2>U3… и предел его общего члена при n®¥ равен 0 (Lim n®¥ Un=0), то ряд сходится, а его сумма не превосходит первого члена: U1³S. Д: Рассмотрим последовательность частичных сумм четного числа членов при n=2m: S2m ... |
|
| 2181. |
Решение уравнений в целых числах ... то оно имеет их бесчисленное множество. Нельзя, конечно, утверждать, что формулами (31) даются все решения уравнения (25). В теории алгебраических чисел доказывается, что все решения уравнения (25) в целых числах можно получить, взяв некоторое конечное и определенное зависящее от и число решений ... |
|
| 2182. |
Решение систем линейных алгебраических уравнений методом Гаусса и Зейделя ... -8.4Результат
вычислений
по методу Гаусса
x1
= 5.0000000000E+00
x2
= -4.0000000000E+00
x3
= 3.0000000000E+00
x4
= -2.0000000000E+00
2.2
Программа
решения систем
линейных уравнений
по методу Зейделя
2.2.1.
Постановка
задачи. Требуется
решить систему
линейных
алгебраических
уравнений с
вещественными ... |
|
| 2183. |
Решение систем дифференциальных уравнений методом Рунге-Куты 4 порядка ... вычислять
четыре раза3.
Выбор метода
реализации
программы
Исходя
из вышеизложенного,
для решения
систем дифференциальных
уравнений мы
выбираем наиболее
точный
метод решения
– метод Рунге-Кутта
4 порядка, один
из самых употребляемых
методов интегрирования
дифференциальных
уравнений ... |
|
| 2184. |
Решение оптимизационной задачи линейного программирования ... переменных (Х3,Х6,Х4,Х5). СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ 1. Смородинский С.С., Батин Н.В. Методы и алгоритмы для решения оптимизационных задач линейного программирования. Ч.1. – Мн.: БГУИР, 1995. 2. Смородинский С.С., Батин Н.В. Методы и алгоритмы для ... |
|
| 2185. |
Метод касательных решения нелинейных уравнений ... стр. ВВЕДЕНИЕ........................................ 5 1. Краткое описание сущности метода касательных ( метода секущих Ньютона).................... 7 2. Решение нелинейного уравнения аналитически .. 9 3. Блок схема программы ... |
|
| 2186. |
Решение некоторых уравнений и неравенств с параметром ... ; зададим прямую а=соnst и будем сдвигать её от -¥ до+¥ 7. Записываем ответ. Это всего лишь один из алгоритмов решения неравенств с параметрами, с использованием системы координат хОа. Возможны и другие методы решения, с использованием стандартной системы координат хОy. ... |
|
| 2187. |
Решение задачи линейного программирования ордана-Гаусса для системы линейных уравнений. Большинство из существующих численных методов решения задач линейного программирования использует идею приведения системы линейных уравнений которая в матричной форме записывается в виде , к более удобному виду с помощью так называемого метода ... |
|
| 2188. |
Задача Дирихле ... + f(xi,yj+1)f(xi,yj-1))/4 6. Теперь если max | F(N+1)*[i,j] - F(N)*[i,j]|< ,взятый по всем точкам области Dh* ,то задача решена; если нет , то выполнять шаг 5 ( пересчитывать функцию F(N)*[i,j] через значения F(N-1)*[i,j]) до тех пор, пока не ... |
|
| 2189. |
Решение задач с помощью ортогонального проектирования ... угол j между прямыми FC и FD является углом между плоскостями П1 и П2 . По определению угла между прямыми 0°<j£90°. Одним из методов решения задач на нахождение угла между плоскостями является поэтапно-вычислительный метод. Применение этого метода может опираться на использование формулы ... |
|
| 2190. |
Решение задач по прикладной математике ... ; 7710 9х1+7х2 ≤ 8910 3х1+10х2 ≤ 7800 где по смыслу задачи х1≥0, х2≥0. Получена задача на нахождение условного экстремума. Для ее решения систему неравенств при помощи дополнительных неизвестных х3, х4, х5 заменим системой линейных ... |
|
| 2191. |
Решение задач на построение сечений многогранников ... плоскостью. (http://www.ssau.ru/books/gubanov/lection1.htm) Основной типовой задачей на эту тему в школьной программе является построение сечения, по трем, заданным на поверхности многогранника, точкам, принадлежащим секущей плоскости. Алгоритм построения такого сечения следующий: 1) ... |
|
| 2192. |
Решение задач линейной оптимизации симплекс – методом ... и имеет единичный базис Б = = E. Решая вспомогательную задачу первым алгоритмом симплекс-метода (описание алгоритма приводится в п.4), в силу ограниченности линейной формы сверху на множестве своих планов () получим, что процесс решения через конечное число шагов приведет к оптимальному опорному ... |
|
| 2193. |
Решение задач линейного программирования ... что решение отсутствует в связи с неог-рачниченностью функции цели. Для практического решения задачи линейного программирования симплекс-методом удобно пользоваться таблицей вида (табл. 11.1): Таблица 1.1 B CB XB A1 … An Q Базисные Целевые ... |
|
| 2194. |
Рациональные уравнения и неравенства ... x — любое число из [0; 1). В) x Î[1; ¥), тогда x + x – 1 = 1; 2x = 2; x = 1 Î[1; ¥). Ответ: x Î[0; 1]. Основные методы решения рациональных уравнений. 1) Простейшие: решаются путём обычных упрощений — приведение к общему знаменателю, приведение подобных членов и так ... |
|
| 2195. |
Расширения полей ... F как векторное пространство над P, т. е. рассматривать векторное пространство +F, +, {wl½l P},, где wl- операция умножения элементов из F на скаляр lP. Определение. Расширение F поля P называется конечным, если F, как векторное пространство над P, имеет конечную размерность. Эта ... |
|
| 2196. |
Корреляционно-регрессивный анализ ... теоpетическому. 2.6 Выбоp вида, оценка паpаметpов функции pаспpеделения значений функции случайных аpгументов и статистический анализ достовеpности получаемых pезультатов. 2.7 Реализация выбpанных статистических методик коppеляционного и линейного pегpессионого анализа паpных зависимостей. 2.8 ... |
|
| 2197. |
Расчет одноступенчатого редуктора ... cedil;4)=5 мм рис2. Коническое зубчатое толщина диска С=(0,1¸0,17)*Rе=7 мм колесо 3.3 Kонструктивные размеры корпуса редуктора толщина стенок корпуса и крышки d = 0,05*Rе+1=3,65 мм; принимаем d = 5 мм d1=0,04*Rе+1=3,12 мм; принимаем d1 = 5 мм толщина фланцев (поясов) корпуса и ... |
|
| 2198. |
Численный расчет дифференциальных уравнений ... y/=z z/=f(x,y,z) Тем самым преобразуются начальные условия: y(x0)=y0, z(x0)=z0, z0=y/0. РЕШЕНИЕ КОНТРОЛЬНОГО ПРИМЕРА Приведем расчет дифференциального уравнения первого, второго и третьего порядка методом Эйлера 1. Пусть дано ... |
|
| 2199. |
Разработка формальной системы ... В также формулы; - если А - формула и хА - переменная, то "xА и $xA - формулы; - других формул нет. Для данной формальной логической системы справедливы следующие аксиомы: 1. E (f+(A, 0), A), 2. E ( f+(A, A), A), 3. & ... |
|
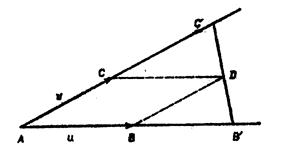
| 2200. |
Различные подходы к определению проективной плоскости ... шести прямых А1А2, А2А3, А3А4, А4А5,
А5А6, А6А1 называемых сторонами.
Мы рассмотрели один из подходов к определению проективной плоскости, а именно определения проективной плоскости на базе трехмерного векторного пространства. Теперь рассмотрим аналитическое определение проективной плоскости. ... |