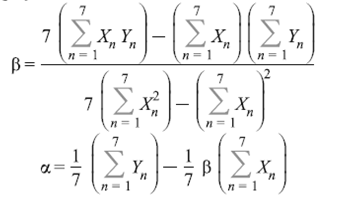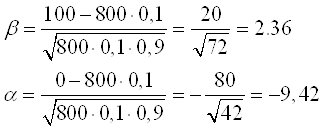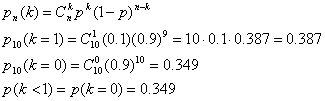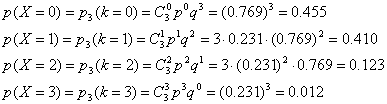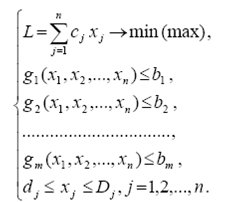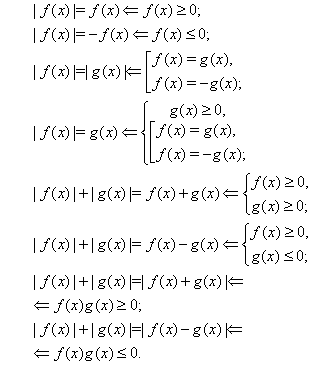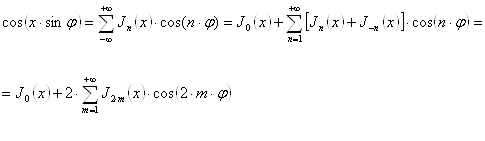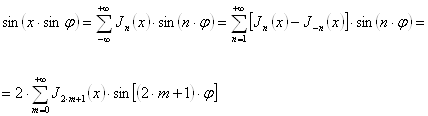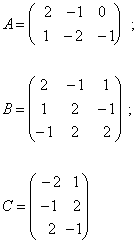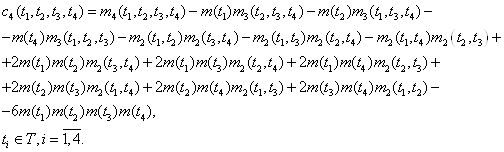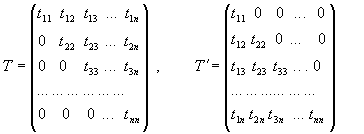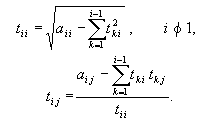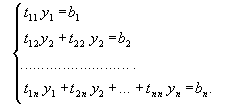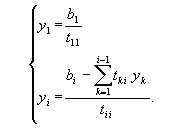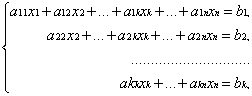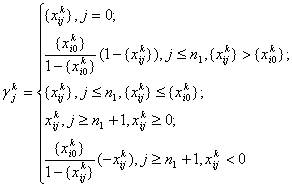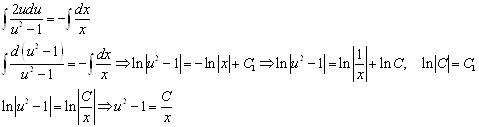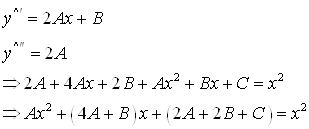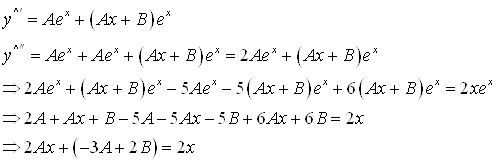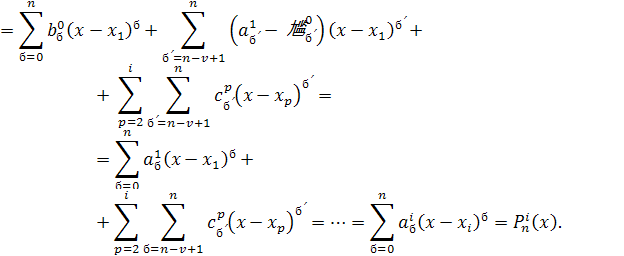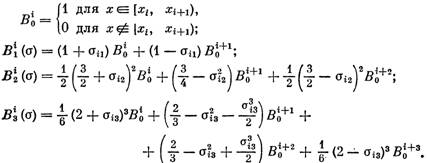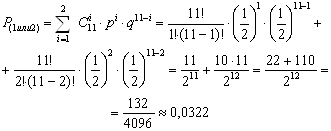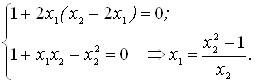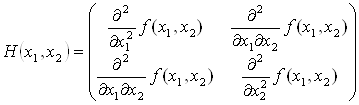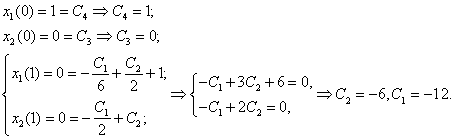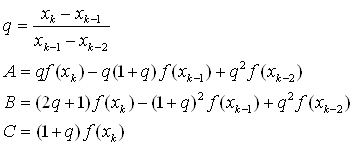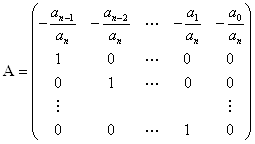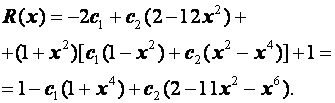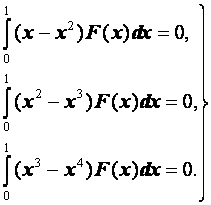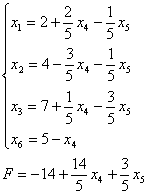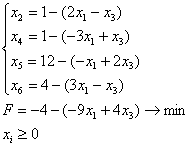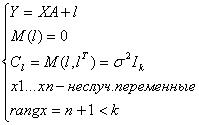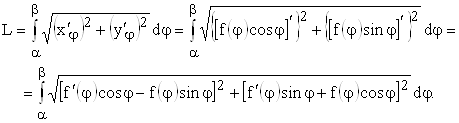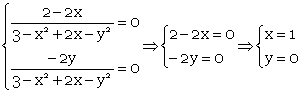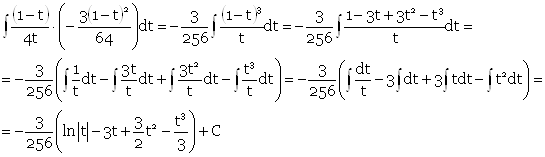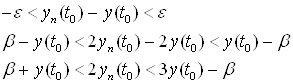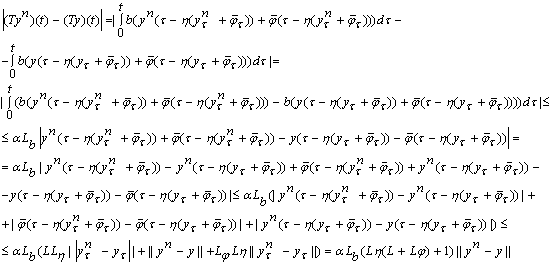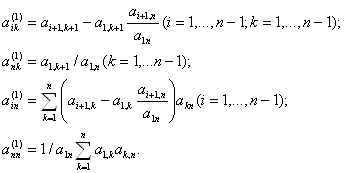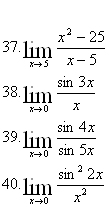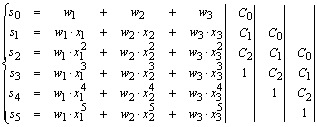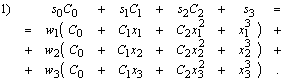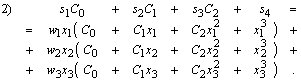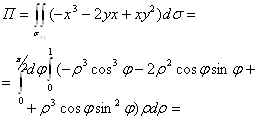| № | Название работы | Скачать |
|---|---|---|
| 401. |
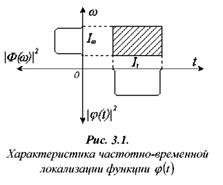
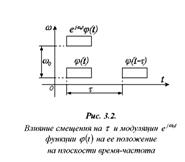
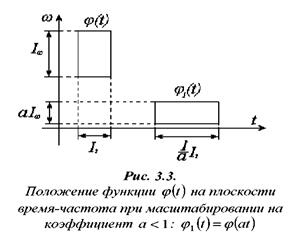
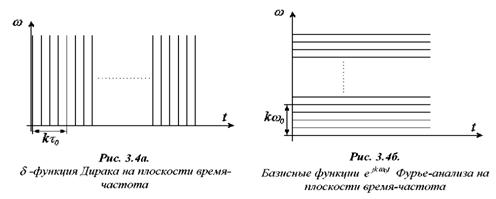
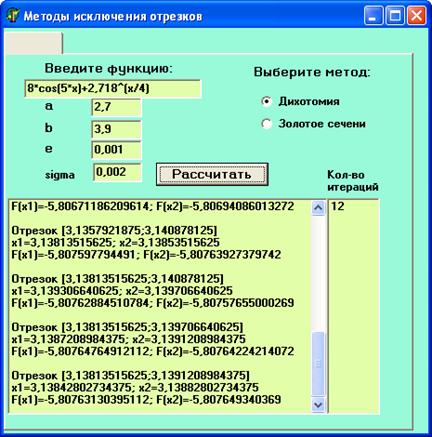
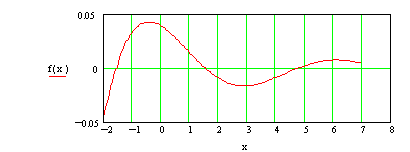
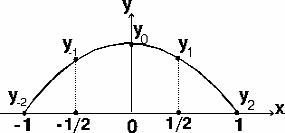
Частотно-временной анализ сигналов ... базисных функций по оси t при расширении или сжатии самой функции и при (рис 3.6) Таким образом, базисные функции для частотно-временного анализа должны обладать следующими свойствами. Ограниченность, т.е. принадлежность L2 . Локализация. Базисные функции вейвлет - анализа, в отличие от ... |
|
| 402. |
Статистическое исследование свойств псевдослучайных чисел получаемых методом Джона фон Неймана ... между ними имеется зависимость, а также наличие периодов в последовательности псевдослучайных чисел. К алгоритмическим методам получения ГСЧ относиться метод серединных квадратов, предложенный в 1946 г. Дж. фон Нейманом. Метод серединных квадратов Имеется некоторое четырехзначное число R0. Это ... |
|
| 403. |
Статистическое изучение взаимосвязей ... распределения исследуемых признаков; 6. количественное выражение факторных признаков, что дает возможность составить модель корреляционной зависимости. 2. Статистические методы выявления наличия корреляционной связи между признаками Для выявления наличия или отсутствия корреляционной связи ... |
|
| 404. |
Статистический анализ условий социально-экономического развития Ленинградской области ... обеспечение формирования показателей, характеризующих уровень достижения целей социально-экономического развития государства, и показателей деятельности федеральных органов исполнительной власти; · интеграцию статистических информационных ресурсов на основе методологической и технологической ... |
|
| 405. |
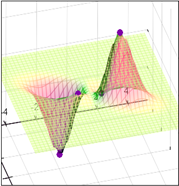
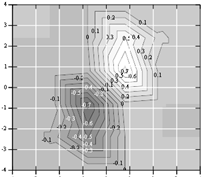
Функция многих переменных ... её производные и аргументы. Обыкновенным называется дифференциальное уравнение, в котором неизвестная функция является функцией одной переменной. Если неизвестная функция является функцией многих переменных, то соответствующее уравнение называется дифференциальным уравнением в частных производных. ... |
|
| 406. |
Статистический анализ выборочных совокупностей ... попадания нормально распределенной случайной величины Х в заданный интервал (х1; х2) определяется по формуле (1): , (13) где Ф(х) – функция Лапласа, . (14) 4. Статистический анализ выборочной совокупности Выборочной совокупностью, или просто выборкой, называют совокупность ... |
|
| 407. |
Статистические расчеты содержания влаги ... понимания средней величины как центра распределения, так как на этом основывается дальнейший статистический анализ. 1.2. Условия применения средних величин в анализе. Обязательным условием расчета средних величин для исследуемой совокупности является ее однородность. Действительно, ... |
|
| 408. |
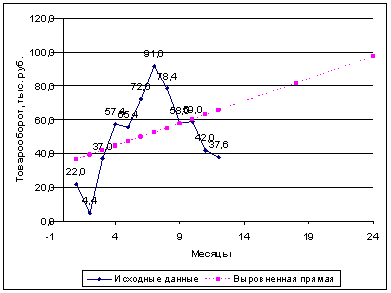
Статистика на предприятии ... итого 4966 0 576 659 4971,96 Задача 10 Имеются данные о производстве изделий и себестоимости единицы изделия на промышленном предприятии за два месяца. Исчислить: Индивидуальные индексы физического объема, себестоимости и затрат. Общие индексы физического объема продукции, ... |
|
| 409. |
Старший и верхний центральный показатели линейной системы ... утверждения 1.3 и определения 1.5 вытекает, что , так как матрица конечномерная. По определению 1.9 P, где (P). 3.2 Старший и верхний центральный показатели для диагональной системы с постоянными коэффициентами. Случай . Исследуем случай, когда матрица системы с постоянными ... |
|
| 410. |
Средние величины ... , тыс. км Середина интервала, тыс. км Число автомашин До 5,0 4,0 40 5,0-7,0 6,0 80 7,0-8,0 7,5 130 8,0 и более 8,5 50 В данном примере средняя величина составляет: _ Х= (4*40+6*80+7,5*130+8,5*50) / (40+80+130+50) =2040/300=6,8тыскм В данном случае размер ... |
|
| 411. |
Сравнительный анализ численных методов ... уравнений методом простых итераций Рисунок 13. Решение уравнения методом Зейделя Раздел 4. Сравнительный анализ методов численного дифференцирования и интегрирования 4.1 Методы численного дифференцирования Необходимость численного дифференцирования может возникнуть при необходимости ... |
|
| 412. |
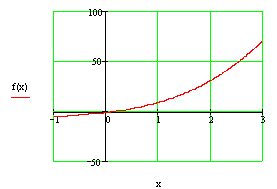
Формула Лапласа. Математическое ожидание ... 78 обрывов нити; б) обрыв нити произойдет не более чем на 100 веретенах. Решение: р = 0,1, тогда q = 1 – p = 1 – 0,1 = 0,9 б) По интегральной формуле Лапласа 4. Участник олимпиады отвечает на 3 вопроса с вероятностью ответа на каждый соответственно 0,6, 0,7, 0,4. ... |
|
| 413. |
Формула Бернулли. Локальная функция Лапласа ... вычислений локальную теорему Муавра-Лапласа. Вероятность того, что событие А наступит ровно k=1600раз, приблизительно равна Здесь - локальная функция Лапласа, значения которой можно взять из таблиц. Получим Ответ :0,0223 4. В коробке лежат 10 исправных и 3 ... |
|
| 414. |
Факторіальні кільця та їх застосування ... кільця M (2, Z). Перевіримо чи буде правим ідеалом Отже правим ідеалом буде. Відповідь: є правим ідеалом. 3. Факторіальні кільця 3.1 Кільця головних ідеалів та евклідові кільця 3.1.1 Подільність в області цілісності В теорії кілець особливої уваги заслуговують кільця, які ... |
|
| 415. |
Сравнительный анализ методов оптимизации ... функций, табличный симплекс – метод. Список используемой литературы 1. А.Г.Трифонов. Постановка задачи оптимизации и численные методы ее решения; 2. Б. Банди. Методы оптимизации. Вводный курс., 1988; 3. Мендикенов К.К. Лекции Приложение А using System; using ... |
|
| 416. |
Фактор-группы. Cмежные классы ... N — нормальная подгруппа группы G тогда и только тогда, когда N/H – нормальная подгруппа фактор-группы G/H. Доказательство. (1) Пусть U Î S(G,H) и пусть ={uH | u Î U} — совокупность смежных классов группы U по своей нормальной подгруппе H. Если uH, uH Î Î, то u, u Î ... |
|
| 417. |
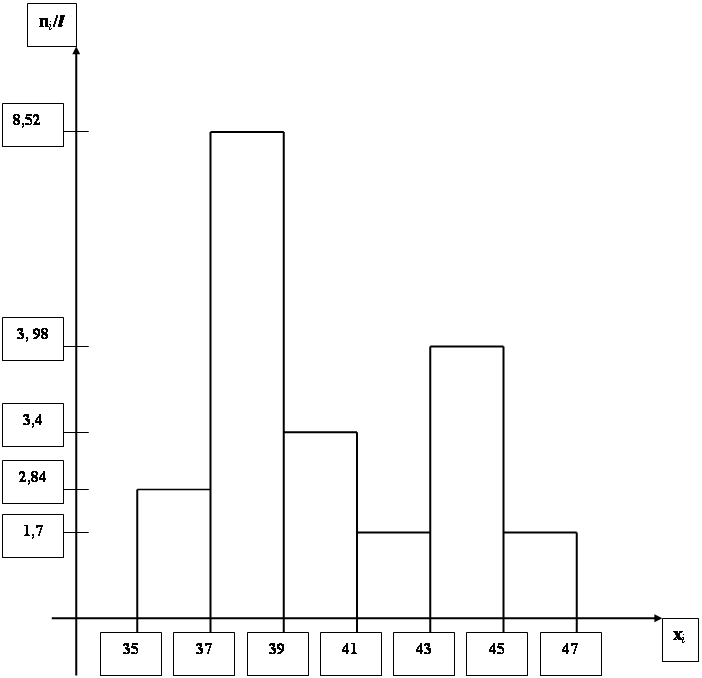
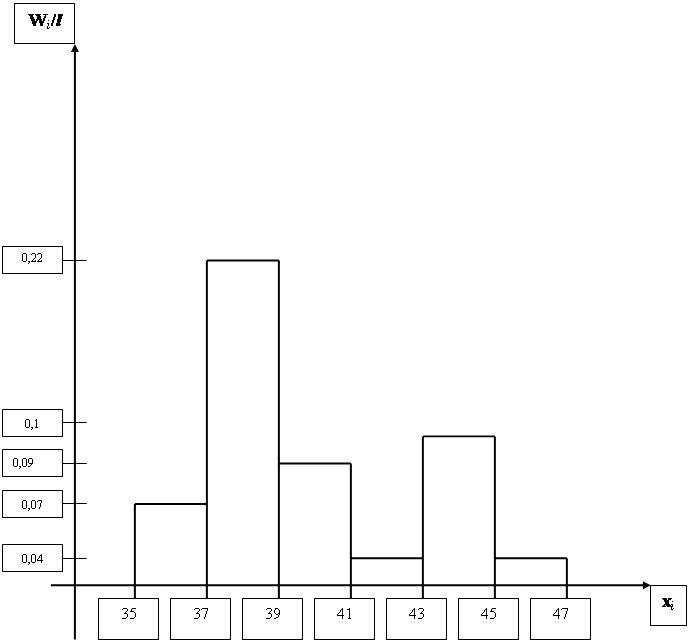
Способы отбора статистических данных ... k ≈ 6,24, тогда длина частичного интервала l ≈ R/k; l ≈ 11/6,24; l ≈ 1,76 - статистическое распределение частот интервального вариационного ряда признака X: 35 -37 37 - 39 39 - 41 41 - 43 43 - 45 45 - 47 5 15 6 3 7 3 - вычислим: а) плотность ... |
|
| 418. |
Устойчивость по Ляпунову ... значений аргументов. Таким образом, точка с координатами должна принадлежать множеству для всех значений на интервале . Устойчивость по Ляпунову Рассмотрим систему дифференциальных уравнений (??) Выделим некоторое решение системы (??) и назовем его невозмущенным ... |
|
| 419. |
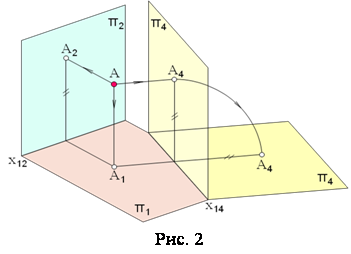
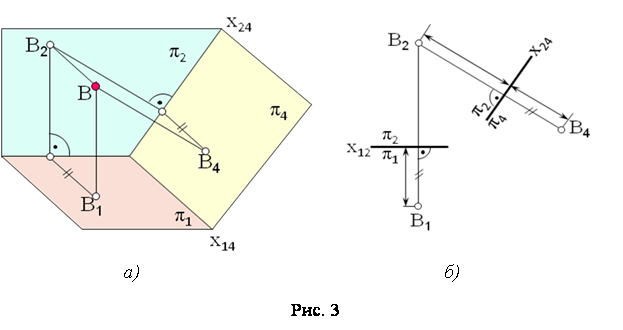
Способи перетворення креслення озв’язування задачі. Щоб досягти частинного розташування геометричних фігур, комплексне креслення перетворюють або перебудовують, виходячи з конкретних умов. Існують два основних способи перетворення проекцій: 1) спосіб заміни площин проекцій; 2) спосіб обертання. При першому ... |
|
| 420. |
Уравнения и неравенства с модулем на централизованном тестировании ... , например, , получаем, что функция принимает только положительные значения. Ответ. . Метод интервалов позволяет решать более сложные уравнения и неравенства с модулями, но в этом случае он имеет несколько иное назначение. Суть состоит в слудующем. Находим корни всех подмодульных выражений и ... |
|
| 421. |
Уравнение и функция Бесселя ... уравнения (4). Полагая ( – не целое) (8) и дополняя это определение для (целое число) формулой: , (8`) получим функцию , удовлетворяющую уравнению Бесселя (4) и во всех случаях линейно независимую от (в случае , где – целое). ... |
|
| 422. |
Упругопластическая деформация трубы ... ЗАДАЧА УПРУГОПЛАСТИЧЕСКОГО ДЕФОРМИРОВАНИЯ ТРУБЫ 2.1 Механическая постановка задачи Рассмотрим упругопластическое состояние трубы радиусов , находящейся под действием внутреннего давления , в случае плоской деформации. Цель данной задачи – определить выражения для компонент ... |
|
| 423. |
Универсальная тригонометрическая подстановка ... удобна замена . При этом: ; ; . Данная подстановка в этом случае дает более простую рациональную дробь, чем с использованием универсальной тригонометрической подстановки. Пусть дан интеграл , где и при этом хотя бы одно из этих чисел нечетное. Допустим, что . Тогда . Далее ... |
|
| 424. |
Умножение матрицы. Теория вероятности ... для вычисления Х2 3-й определитель для вычисления Х3 Х1 = Δ1/Δ ≈ 1 Х2 = Δ2/Δ ≈ 2 Х3 = Δ3/Δ ≈ - 2 Задание 3 Теория вероятности (события). Известно, что курс евро к рублю может возрасти с вероятностью 0,55, а курс доллара к рублю ... |
|
| 425. |
Уменьшение оценки взаимной спектральной плотности стационарного случайного процесса ... (2.4), Видим, что Таким образом, справедливо следующее утверждение. Теорема 2.1. Оценка взаимной спектральной плотности стационарного в широком смысле случайного процесса , задаваемая равенством (2.5), удовлетворяет соотношению , , при условии, что справедливо ... |
|
| 426. |
Узагальнена функція Гріна ... К похідна має розрив першого роду зі стрибком 1/p(s): -. 4. Для кожного фіксованого функція ортогональна до функції : . 5. Сформулюємо алгоритм відшукання узагальненої функції Гріна. · Знаходимо таку фундаментальну систему , лінійного однорідного рівняння (1), щоб ... |
|
| 427. |
Тригонометрические уравнения и неравенства ... тригонометрических уравнений. В третьем разделе рассматриваются нестандартные тригонометрические уравнения, решения которых основано на функциональном подходе. В четвертом разделе рассматриваются тригонометрические неравенства. Подробно рассмотрены методы решения элементарных тригонометрических ... |
|
| 428. |
Три задачи по теории чисел ... числах. Следствие Система уравнений неразрешима в рациональных числах, где - переменные (не равные 0). Задача 3 Утверждение (n=3) Уравнение a3 = b2 + cd2 (1) где с = const, имеет следующее решение: a = α2 + cβ2 b ... |
|
| 429. |
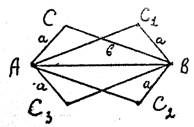
Трансформация преобразований ... , в силу произвольности точки А, искомая трансформация есть косое сжатие с осью f(q), направлением f(l) и коэффициентом k. 17. Решение задач с помощью трансформации преобразований Задача 1. Даны правильные одинаково ориентированные треугольники OAB, OCD, OEF. Доказать, что середины M, N, P ... |
|
| 430. |
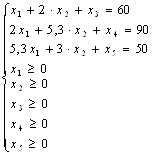
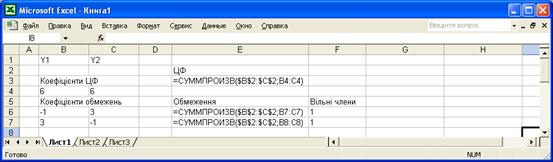
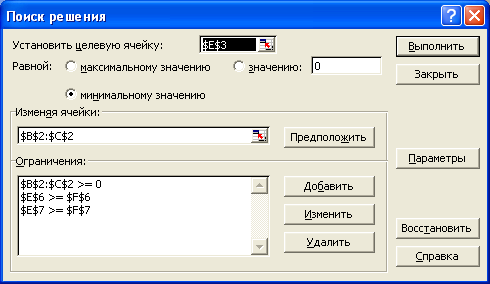
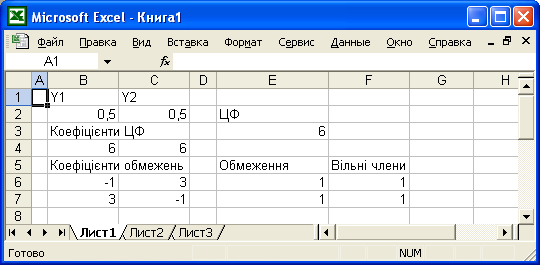
Транспортная задача линейного программирования ... Требуется в области допустимых решений системы уравнений (2.1) и (2.1.1) найти решение, минимизирующее линейную функцию (2.4). Таким образом, мы видим, что транспортная задача является задачей линейного программирования. Для ее решения применяют также симплекс-метод, но в силу специфики ... |
|
| 431. |
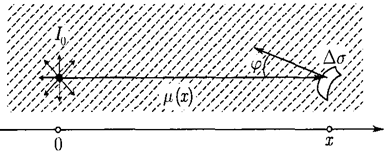
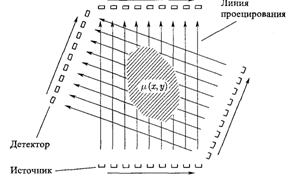
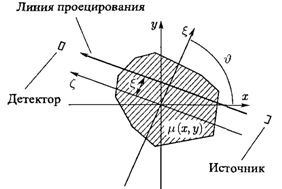
Традиционные методы вычислительной томографии ... которая в каком-то смысле хорошо описывала бы искомую функцию . Непосредственная подстановка "зашумленных" проекционных данных [7] в указанный вычислительный алгоритм приводит к большим искажениям в . Дело в том, что задача реконструкции относится к так называемым некорректным задачам [8]. ... |
|
| 432. |
Точные методы численного решения систем линейных алгебраических уравнений ... : , где матрица коэффициентов системы; - вектор неизвестных; - вектор свободных членов. 2. Точные методы решения
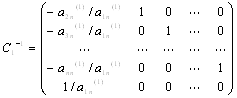
СЛАУ Метод главных элементов. Пусть дана система линейных алгебраических уравнений. Рассмотрим расширенную матрицу, состоящую из коэффициентов системы a[i,j] и свободных ... |
|
| 433. |
Точные методы решения систем линейных алгебраических уравнений (СЛАУ) ... метода к конкретной задаче (анализ) Составляя задачи на языке программирования Borland C++ Builder 6 для реализации точных методов решения СЛАУ я учитывал разное количество уравнений в системе (размерность матрицы задавал равным nxn). Но для проверки результатов использовал уравнения (для ... |
|
| 434. |
Топологические пространства ... ; F1. € Аналогично доказывается Теорема 1.4. Если связное множество М содержится в объединении двух дизъюнктных открытых множеств О1 и О2 топологического пространства Х, то оно целиком содержится только в одном из множеств, входящих в объединение. Теорема 1.5. Пусть f : Х→Y ... |
|
| 435. |
Топологическая определяемость верхних полурешёток ... любого конечного числа множеств из принадлежит , т.е. . 3. Объединение любого семейства множеств из принадлежит , т.е. . Таким образом, топологическое пространство – это пара <, >, где - такое множество подмножеств в , что и замкнуто относительно конечных пересечений и ... |
|
| 436. |
Теория случайных функций ... экспоненциально с параметром m. Тип резервирования - ненагруженный. Для описания состояния системы введем двумерный случайный процесс n(t) = (x(t), d(t)) с координатами, описывающими: - функционирование элементов x(t) Î {0, 1, 2} - число неисправных элементов; - функционирование КПУ ... |
|
| 437. |
Теория поля и элементы векторного анализа ... уравнение (8) упрощается (8а) и его решение имеет вид: (9) Следовательно, искомое поле равно: Интегральные соотношения теории векторного поля 1. Теорема Остроградского-Гаусса 2. Теорема Стокса ... |
|
| 438. |
Теория остатков ... R по мультипликативной системе S тоже является евклидовым. Нормой дроби x из S-1R принимается , где dR — евклидова норма в R, а dS — норма в S-1R. Деление с остатком определяется так. Пусть есть две ненулевые дроби x = r / t и y из S-1R. По определению нормы в S-1R существует элементы u в R и s ... |
|
| 439. |
Теория о бесконечности простых чисел-близнецов ... примерно равно a/ln x. Соответственно вероятность того, что два числа вблизи Х оба окажутся простыми, приблизительно равна 1/lnІ x. Ожидаемое же количество простых чисел-близнецов в интервале от x до x + a приблизительно равно a/lnІ x. На самом деле в реальности, ожидаемая величина немного больше, ... |
|
| 440. |
Поверхні ... Ф по деякій лінії l. Точки цієї лінії будують за допомогою допоміжних площин. Так, площина Σ перетинає задану поверхню по кривій лінії и, а січну площину Г – по прямій а. Ці лінії перетинаються в точках М і N, які належать шуканій лінії перетину l. Повторюючи указаний спосіб декілька разів, ... |
|
| 441. |
Побудова скінченних множин ... -ТН Селін Ігор Керівник: д.т.н. Ляхов Олександр ЛогвиновичПолтава 2010 Постановка задачі УМОВА ЗАДАЧІ: Дано скінчені множини А, В, С. Побудувати множини , , , , , Множина - це деяка визначена сукупність елементів чи об’єктів. Списковий спосіб подання множини - перелік усіх елементів у ... |
|
| 442. |
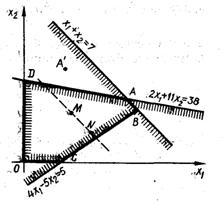
Побудова математичної моделі задачі лінійного програмування ... до третього – х5. Додаткові змінні вводяться зі знаками „+”, оскільки обмеження мають тип „”. Математична модель задачі у канонічній формі: за умов Завдання 2 Розв’язати задачу лінійного програмування графічним методом за умов Розв’язання. В декартовій системі ... |
|
| 443. |
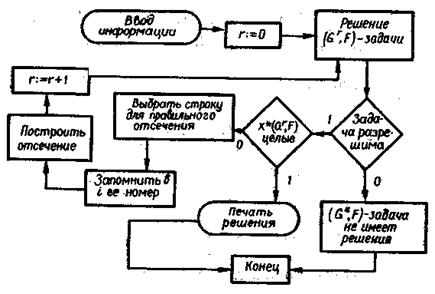
Методы отсечения ... (многоугольника) условий, что было характерно для задач линейного программирования. 2. Теоретические основы методов отсечения Запишем общую задачу целочисленного программирования: в области, определенной условиями (11) (12) - целые, ... |
|
| 444. |
О теории вероятностей ... представление об изучаемом распределении. Далее необходимо исследовать числовые характеристики распределения (аналогичные характеристикам распределения теории вероятностей): характеристики положения (средняя арифметическая, мода, медиана); характеристики рассеяния (дисперсия, среднее квадратическое ... |
|
| 445. |
Интегралы. Дифференциальные уравнения ... уравнения го порядка называется такое его решение , которое является функцией переменных и произвольных независимых постоянных . Частным решением дифференциального уравнения называется решение, получаемое из общего решения при некоторых конкретных числовых значениях постоянных . Теорема. ... |
|
| 446. |
Интеграл дифференциального уравнения ... │х│>6. 6. Определить точки разрыва функции у=(8х+2)/(16х2-1). Отв. Точки х1=–1/4 и х2=1/4. Задача 1 Найти общий интеграл дифференциального уравнения: Решение Выполним разделение переменных, для этого разделим обе части уравнения на : Проинтегрируем обе ... |
|
| 447. |
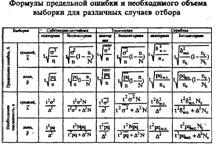
Выборочное наблюдение ... , что средний разряд рабочих механического цеха находится в пределах , . 4 Определение необходимой численности выборки В практике проведения выборочного наблюдения возникает потребность в определении численности выборки, которая необходима для обеспечения определенной точности расчета ... |
|
| 448. |
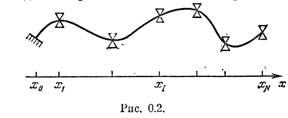
Базисные сплайны ... представлением сплайна в виде суммы усеченных степенных функций. Итак, множество является конечномерным пространством размерности §2. Базисные сплайны с конечными носителями В математическом анализе встречаются конструкции, связанные с финитными функциями, т. е. гладкими функциями, ... |
|
| 449. |
Геометрические построения на плоскости ... значения в вышеприведенные уравнения, то они удовлетворят последним. Путь, которым Мальфатти нашел решения, чрезвычайно сложен, как он сам указывает. Геометрическое же построение величин х, у, z представляется чрезвычайно простым, ибо вследствие чего отрезки эти, равно как и отрезки s, t, r, ... |
|
| 450. |
Учение о параллельности. Открытие неевклидовой геометрии ... показали его современники. Последнее «доказательство» он опубликовал в 1823 году, за три года до первого доклада Лобачевского о новой геометрии. Открытие неевклидовой геометрии В первой половине XIX века по пути, проложенному Саккери, пошли сразу три математика: К.Ф. ... |
|
| 451. |
Уравнение линии на плоскости ... отношение Прямые называются асимптотами гиперболы. Если , то гипербола называется равнобочной. Из уравнения получаем пару пересекающихся прямых и . Параболой называется геометрическое место точек на плоскости, от каждой из которых расстояние до данной точки, называемой фокусом, равно ... |
|
| 452. |
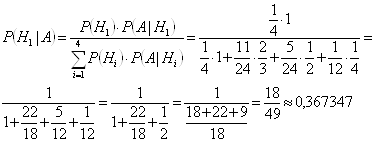
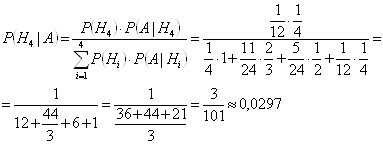
Теория вероятности ... отлично, Н2 – студент подготовлен хорошо, Н3 – студент подготовлен посредственно, Н4 – студент подготовлен плохо. До начала экзамена априорные вероятности этих гипотез: , , , . После экзаменационной проверки одного из студентов оказалось, что он ответил на все три вопроса. Найдем условные ... |
|
| 453. |
Представление функции рядом Фурье ... ряды Фурье ведут себя в точке одинаково: либо оба сходятся, и притом к одной и той же сумме, либо оба расходятся. Представление функций рядом Фурье Наложим на функцию f(x) более тяжелое требование, а именно—предположим ее кусочно-дифференцируемой в промежутке . Тогда имеет место общая теорема: ... |
|
| 454. |
Правовая статистика ... значень 1% приросту; середнього абсолютного приросту, середнього темпу зростання і приросту. Напишіть короткий аналітичний огляд зміни в динаміці правового показника і причин цієї зміни. Вихідні дані взяті з навчального посібника: ст 280-295, стовпець 10, 13, рядки 11-40. Таблиця 1 ... |
|
| 455. |
Понятие многомерной случайной величины ... считаются практически невозможными. В этом и состоит правило «трех сигм»: если случайная величина распределена по нормальному закону, то ее отклонение от математического ожидания практически не превышает±3σ. Понятие о теоремах, относящихся к группе «центральной предельной теоремы» В теоремах ... |
|
| 456. |
Передаточные функции одноконтурной системы ... его настройки: ; ; . Практическая работа № 4 Дана одноконтурная АСР. Требуется определить: · передаточные функции регулятора и объекта управления, · передаточную функцию разомкнутой системы W∞(s), · характеристическое выражение замкнутой системы (ХВЗС), ... |
|
| 457. |
Основы статистики ... сумма накопленных частот составляет половину (или больше) всей суммы частот ряда. 23. Вариация признака Для хар-ки размера вариации в статистике прим-ся абсолютные показатели вариации: размах вариации, среднее линейное отклонение, среднее квадратическое отклонение и дисперсия. Размах вариации ... |
|
| 458. |
Методы оптимизации функций многих переменных ... , кроме того, и информацию о вторых производных функции f (x) (метод Ньютона и его модификации). Метод конфигураций (Хука - Дживса) Следует выделить два этапа метода конфигураций: 1) исследование с циклическим изменением переменных и 2) ускорение поиска по образцам. Исследующий поиск начинается ... |
|
| 459. |
Методы оптимизации при решении уравнений ... а подставляя 1-е в третье, получим: Таким образом, решение имеет вид: Задание №4 Используя метод динамического программирования найти оптимальное уравнение для системы A B t0 tf F a b 0 1 0 0 0 1 0 ∞ 0 1 0 0 2 1 ... |
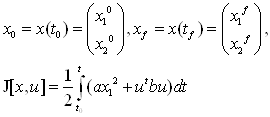
|
| 460. |
Методы нахождения корней полиномов ... откуда Знак перед корнем выбирают с таким расчетом, чтобы получить наибольшее значение знаменателя. Еще один метод, который применяют для поиска корней полиномов, – метод сопровождающей матрицы (companion matrix). Можно доказать, что матрица , называемая сопровождающей матрицей для ... |
|
| 461. |
Методы коллокаций и Галеркина ... nbsp;найдем систему Решая эту систему, отыщем y0=0.967, y1=0.721. Итак, сравним: метод коллокации дает y0=0.957, а метод сеток y0=0.967. Метод Галеркина Пусть дано дифференциальное уравнение с линейными краевыми условиями ,
(2.62) ... |
|
| 462. |
Методология изучения темы "Признаки равенства треугольников" ... треугольника АВС равен 50 м, а периметр треугольника ABD равен 40 м. Определить высоту BD. УРОК 6 Обобщающий урок по теме «Признаки равенства треугольников» Все учителя в начале изучения темы определяют для себя и для учащихся требования, предъявляемые к знаниям учащихся в конце ее ... |
|
| 463. |
Методические указания и контрольные задания для студентов-заочников ... и достаточным условием? 11.Что такое точка перегиба? 12.Какие бывают асимптоты? Приведите примеры. КОНТРОЛЬНАЯ РАБОТА №1 Задача 1. Даны векторы a и b. Найти вектор c = a + b и скалярное произведение (a ·b), где a = {1, M + 4, -1, N - 5},b = {-M + 5, -1, 5 – N, 2} . Задача 2. Даны ... |
|
| 464. |
Логика высказываний ельство ее справедливости следует начать с приведения ее в нормальную конъюнктивную форму. В v С, A v -B v -C, -A => 0 P1 P2 P3 Справа от каждого нового дизъюнкта будем писать номера используемых дизъюнктов, получим: № п/п Выводы Почему 1. А Р1, Р2 2. 0 P3, 1 ... |
|
| 465. |
Логарифмические уравнения ... функция выпукла вверх, а если a (0;1) - выпукла вниз. Следующие утверждения (см., например, [1]) используются при решении логарифмических уравнений. Утверждение 2. Уравнение loga f(x) = loga g(x) (a > 0, a ≠ 1) равносильно одной из систем (очевидно, выбирается та система, неравенство ... |
|
| 466. |
Линейные функции рое запишем в виде Из уравнения Получим прямую с угловым коэффициентом Значение соответствует прямой, которая отсекает треугольник площадью S=4,5 от третьего координатного угла.. № 3. Даны вершины треугольника А (2,1,0), В (3,-1,1) и С (1,2,-4). Записать общее уравнение ... |
|
| 467. |
Линейные уравнения и их свойства ... по базису из условия выполнения векторного равенства , которое для соответствующих координат запишется Полученную квадратную систему линейных уравнений относительно неизвестных решим по формулам Крамера. Вычислим определители3-го порядка: Тогда по формулам Крамера находим ... |
|
| 468. |
Линейное и нелинейное программирование ... в реальных системах, т. е. использованию моделей, более адекватных исследуемым явлениям. Библиографический список 1 Лященко И.Н. Линейное и нелинейное программирования / И.Н.Лященко, Е.А.Карагодова, Н.В.Черникова, Н.З.Шор. – К.: «Высшая школа», 1975, 372 с. 2 Методические указания для ... |
|
| 469. |
Линейно упорядоченное пространство ординальных чисел ... замкнутых множеств А и В существуют непересекающиеся открытые множества U и V такие, что АU, BV. ГЛАВА 2. Линейно упорядоченное пространство ординальных чисел. §1.ВПОЛНЕ УПОРЯДОЧЕННЫЕ МНОЖЕСТВА И ИХ СВОЙСТВА. Рассмотрим вполне упорядоченные множества и их ... |
|
| 470. |
Линейная модель множественной регрессии ... типов: ЛММР РМ с переменной структурой (фиктивные переменные) Нелинейные РМ Модели временных рядов Системы линейных одновременных уравнений 1. ЛММР Предположим, что по ряду регионов множественная регрессия величины импорта на определенный товар у относительно отечественного производства х1, ... |
|
| 471. |
Конечные группы с заданными системами слабо нормальных подгрупп ... выше понятия слабой квазинормальности. Таким образом, задача изучения групп с заданной системой слабо квазинормальных подгрупп вполне актуальна, ее реализации посвящена данная работа. 1. Определение и общие свойства слабо нормальных подгрупп Определение. Подгруппа группы называется слабо ... |
|
| 472. |
Доказательство великой теоремы Ферма для четных показателей степени В2m /3/ Для доказательства великой теоремы Ферма используем алгебраическое доказательство теоремы Пифагора. АЛГЕБРАИЧЕСКОЕ ДОКАЗАТЕЛЬСТВО ТЕОРЕМЫ ПИФАГОРА (Решение уравнения теоремы Пифагора в целых числах) Теорема Пифагора формулируется следующим образом: в прямоугольном ... |
|
| 473. |
Доказательство великой теоремы Ферма целое положительное число, большее двух, не имеет решения в целых положительных числах. Суть Великой теоремы Ферма не изменится, если уравнение /1/ запишем следующим образом: Аn = Сn - Вn /2/ Рассмотрим решения уравнений /1/ и /2/ при нечетных значениях показателя степени n и ... |
|
| 474. |
Доказательство великой теоремы Ферма ... , что статья доступна для понимания не только суперматематикам, но и обычным людям, проявляющим интерес к данной проблеме. Доказательство теоремы Ферма. Посвящаю моему учителю математики Зильбербергу Осипу Михайловичу. 1. Введение. Математика – это абстрактная наука ... |
|
| 475. |
Доказательство великой теоремы Ферма ... не имеет решения в целых положительных числах при нечетном показателе степени n >2. ДОКАЗАТЕЛЬСТВО ВЕЛИКОЙ ТЕОРЕМЫ ФЕРМА ДЛЯ ЧЕТНЫХ ПОКАЗАТЕЛЕЙ СТЕПЕНИ Доказательство строим аналогично вышеизложенному доказательству для нечетных показателей степени. Любое четное число, за исключением ... |
|
| 476. |
Доказательство великой теоремы Ферма х. Суть великой теоремы Ферма не изменится, если уравнение (1) запишем следующим образом: Аn = Сn - Вn (2) Для доказательства великой теоремы Ферма предварительно докажем вспомогательную теорему (лемму). ЛЕММА: Любое натуральное число N>2 в любой степени равно разности квадратов двух ... |
|
| 477. |
Доказательство бесконечности некоторых видов простых чисел ... способ, с помощью которого можно решить часть этих проблем. Рассмотрим многочлен который при значениях от до , дает бесконечный ряд натуральных чисел (1) А также рассмотрим ряд простых чисел (2) некоторого типа, о котором известно, что он бесконечен. Пусть простые числа (2) делят числа (1) и ... |
|
| 478. |
Длина окружности и площадь круга вого материала. Оборудование: плакаты с формулами длины окружности и площади круга. I. Устная работа (актуализация знаний) 1. Решить № 858 (а; б; в) устно и № 859 (в; г). № 858 (а; б; в) № 859 (в; г). 2. Решить задачу, повторив формулу длины окружности с = pd: определите диаметры ... |
|
| 479. |
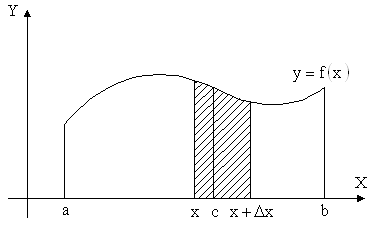
Длина дуги кривой в прямоугольных координатах ... откуда: . Так же как и в неопределенном интеграле, данная формула требует правильного выбора множителей и . 5. Длина дуги кривой в прямоугольных координатах При вычислении длины кривой линии может быть использована та же методика, что и при вычислении площадей криволинейных трапеций, то есть ... |
|
| 480. |
Дифференцирование. Интегрирование ... + 2x – y2) имеет экстремум в точке М (1; 0) – максимум, т. к. A< 0. Задание 4. Вычислить неопределенные интегралы, результат проверить дифференцированием a) Решаем методом замены переменной. Положим , тогда , Таким образом, получаем ... |
|
| 481. |
Дифференциальные уравнения с запаздывающим аргументом ... для малых положительных t существует два различных решения: Действительно, проверим, удовлетворяют ли эти функции уравнению: Значит, система имеет два различных решения. Это происходит потому что при малых t аргумент оказывается в окрестности -1, а при этих значениях началь |
|
| 482. |
Геометрические векторы ... величине вектора, а направление - совпадает с направлением векторной величины. В дальнейшем эти отрезки и будем называть геометрическими векторами. При изображении вектора одна точка, ограничивающая вектор, называется началом, а вторая - концом вектора. В конце вектора ставится стрелка. Для ... |
|
| 483. |
Геометрии Галилея и Минковского как описания пространства-времени ... говоря, каковы его основные «исходные компоненты». Тогда станет видно, как эти «компоненты» могут сочетаться в иных комбинациях, образуя иные типы пространств. 2.1 Основные понятия описания пространства-времени 2.1.1 Геометрические векторы и линейные операции над ними Для математического ... |
|
| 484. |
Вычислительная математика ... 0.9 1.0 1.43333 1.63232 1.89648 2.24790 2.71827 5×10-7 2×10-6 3×10-6 6×10-6 2×10-5 Задачи к зачету по курсу “Вычислительные методы” Указание. Каждый студент вначале должен определить параметр своего контрольного задания, s = log10 ... |
|
| 485. |
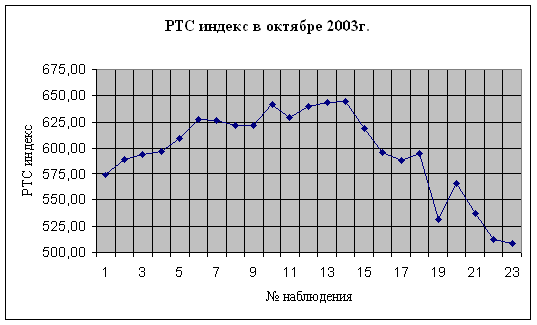
Вычисления по теории вероятностей ... ; n=220 1215 7354,25 Найдем оценки параметров распределения: = = 5,523 2= 2 = 2,925 = = 1,71 4. все вычисления для проверки гипотезы о распределении занесем в таблицы. № Интервалы Частоты, mi t1 t2 Ф(t1) Ф(t2) pi 1 -∞ ... |
|
| 486. |
Вычисление характеристических многочленов, собственных значений и собственных векторов ения собственных чисел и собственных векторов сводится к нахождению коэффициентов характеристического уравнения, нахождению его корней и нахождению нетривиального решения системы. Метод Данилевского Простой и изысканный метод нахождения характеристического многочлена предложил А.М.Данилевский ... |
|
| 487. |
Вычисление пределов функций, производных и интегралов ... : Исследуемая функция в промежутке – возрастает – убывает - возрастает 5. Найдем промежутки выпуклости графика функции, ее точки перегиба. Найдем вторую производную функции: при - точка перегиба Для , следовательно, график функции на этом интервале ... |
|
| 488. |
Вычисление пределов ... преподаватель _____________(___................. __) (Подпись) (ФИО) «_______» _________________200___г. Цель работы: 1. Формировать умения и навыки вычисления пределов 2. Формировать умения и навыки самостоятельного умственного труда 3. Прививать умения и навыки работы со ... |
|
| 489. |
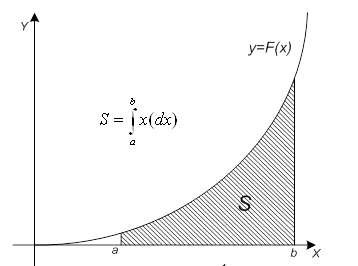
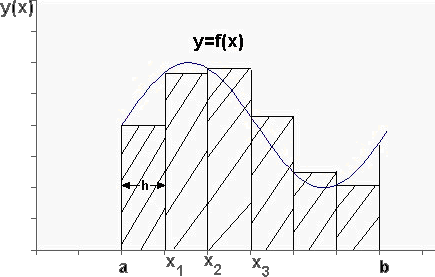
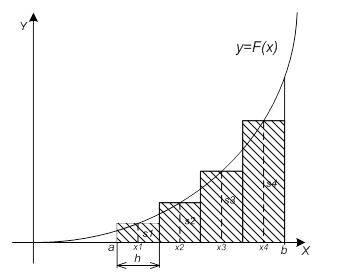
Вычисление определенных интегралов. Квадратурные формулы ... функции. В качестве квадратурного выражения обычно выбирают взвешенную сумму значений подынтегральной функции. 1. Вычисление определенных интегралов Количество параметров квадратурного выражения тесно связано со степенью подынтегральной функции, если последняя может быть описана ... |
|
| 490. |
Вычисление определенного интеграла ... ) повышается точность приближенного вычисления интегралов Задание на лабораторную работу 1) Написать программы вычисления определенного интеграла методами: средних, правых прямоугольников, трапеции и методом Симпсона. Выполнить интегрирование следующих функций: 1. f(x)=x f(x)=x2 ... |
|
| 491. |
Вычисление наибольшего, наименьшего значения функции в ограниченной области ... наименьшее значения являются либо локальными экстремумами, либо граничными точками области. Следовательно, чтобы найти наибольшее и наименьшее значения функции z = f ( x , y ) в ограниченной замкнутой области D, следует вычислить значение функции в критических точках области D, а также наибольшее и ... |
|
| 492. |
Вычисление интегралов методом Монте-Карло ... случайных чисел с хорошим равномерным распределением, на использовании которых основан этот метод. Метод Монте – Карло это статистический метод. Его используют при вычислении сложных интегралов, решении систем алгебраических уравнений высокого порядка, моделировании поведения элементарных частиц, ... |
|
| 493. |
Высшая математика. Матрица ... оператор А действует в R3 → R3 по закону Ax = (- х1 + 2х2 + x3 , 5х2 , 3х1 + 2х2 + х3 ), где х( х1, х2, х3 ) – произвольный вектор .(125.РП). Найдите матрицу А этого оператора в каноническом базисе . Докажите , что вектор х(1,0 ,3) является собственным для матрицы А .(Т56). Найдите собственное ... |
|
| 494. |
Высшая математика для менеджеров ... xо является точкой локального минимума (максимума) функции f(x). Если же =0, то нужно либо пользоваться первым достаточным условием, либо привлекать высшие производные. На отрезке [a,b] функция y = f(x) может достигать наименьшего или наибольшего значения либо в критических точках, либо на концах ... |
|
| 495. |
Высшая математика в экономике ния плана по изготовлению стенок первого, второго, третьего и четвертого вида в количестве соответственно x1, x2, x3 и x4 штук; 2) провести подсчеты для значений x1 = 50, x2 = 30, x3 = 120 и x4=80. Решение: составим условия для определения числа составных частей в зависимости от числа и вида ... |
|
| 496. |
Высшая математика в профессиональной деятельности военного юриста ... и французский языки, а также мусульманское и международное право. Целью данной работы является освещение предмета высшей математики в профессиональной деятельности военного юриста. Работа включает не только теоретические аспекты применения методов высшей математики в военной юриспруденции, но и ... |
|
| 497. |
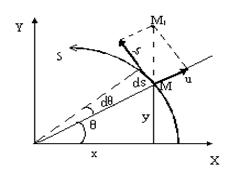
Визначення та обчислення довжини дуги плоскої кривої в декартових та полярних координатах. Площа поверхні ... формулу, узявши до уваги, що рівняння кривої в полярних координатах можна записати як параметричні з параметром q : і використавши формулу (10.10). Приклад 1. Обчислити довжину кривої, заданої рівнянням Розв‘язок. Досить обчислити довжину дуги, що обмежує зверху заштриховану на рис.10.7 ... |
|
| 498. |
Великая теорема Ферма – два коротких доказательства ... , то есть . Из условий эквивалентности или анализа причин неэквивалентности этих уравнений следуют те же выводы. Это доказательство опубликовано в 1993 г. в журнале РАН «Вопросы истории естествознания и техники», №3. Со стороны оппонентов не поступило никаких возражений по существу, ... |
|
| 499. |
Велика теорема Ферма ... квадратів. Хоча Ферма вніс великий внесок до розвитку теорії чисел алгебри, докази його доводів майже ні в одному випадку знайдені не були (доведення Великої теореми Ферма для n=4 – виключення, оскільки в рукописах воно було). Деякі виводи, зроблені Ферма, були і зовсім помилковими, але теореми, ... |
|
| 500. |
Векторные линии в векторном поле ... Векторные линии представляют собой семейство эллипсов Вычислить длину дуги линии ; Решение: Найдем производные ; Длина дуги кривой в параметрических координатах равна: Вычислить поток векторного поля через поверхность Решение: По определениюпотока векторного ... |