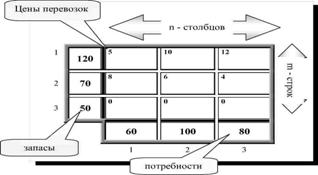
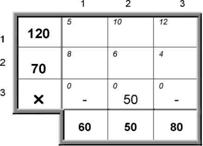
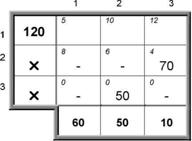
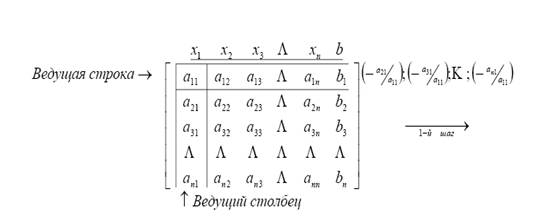
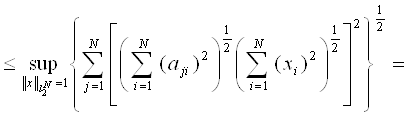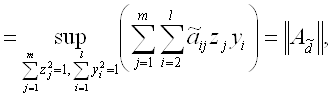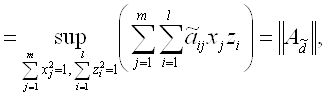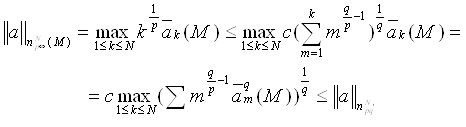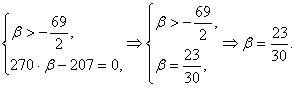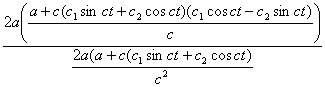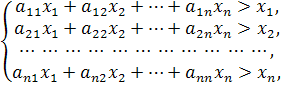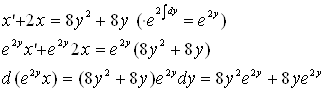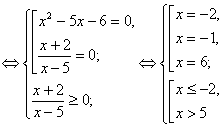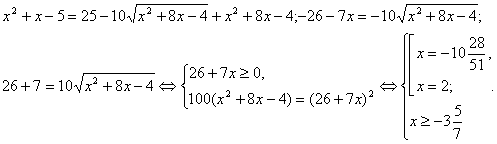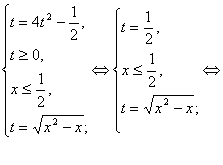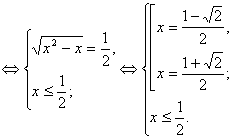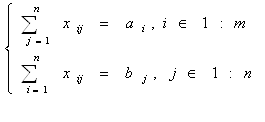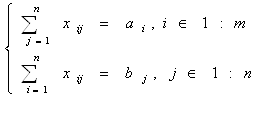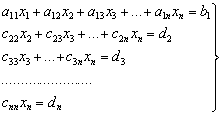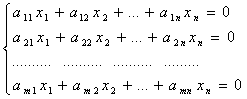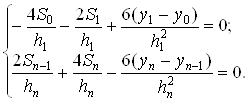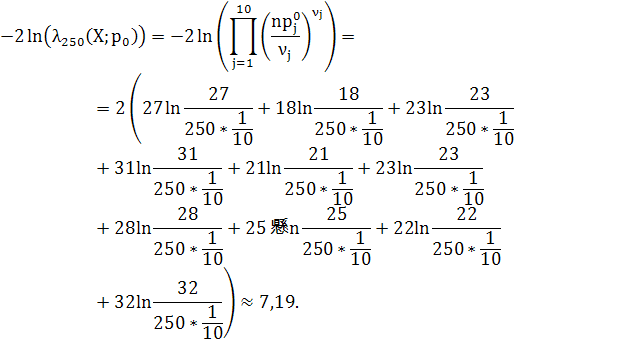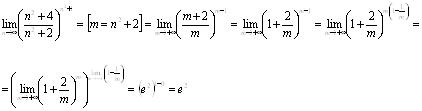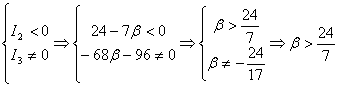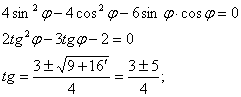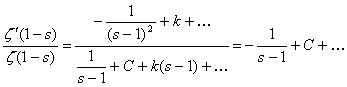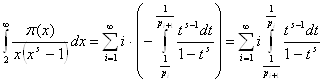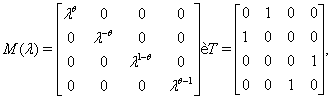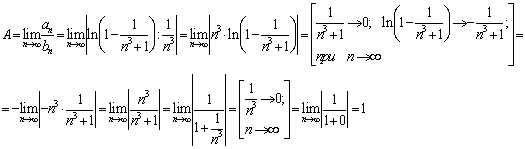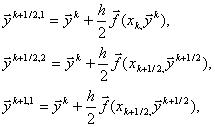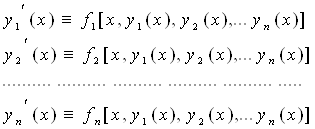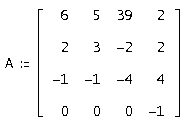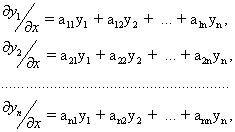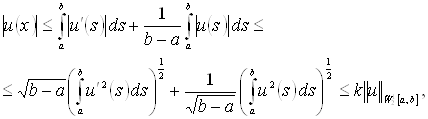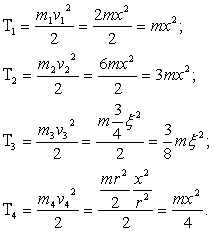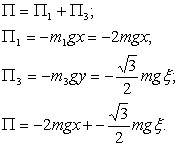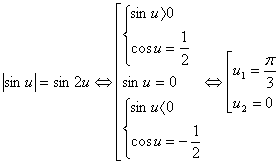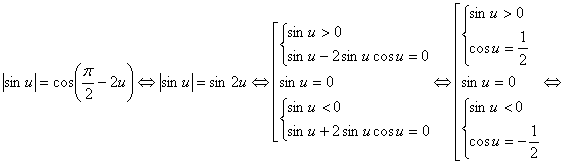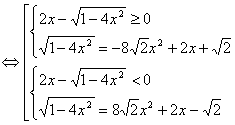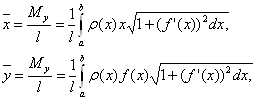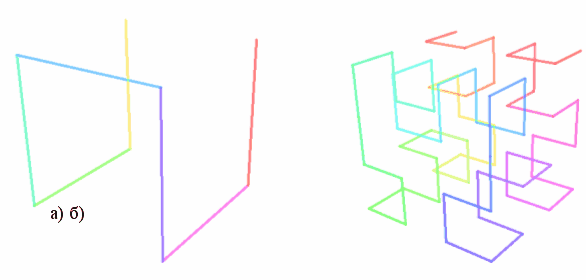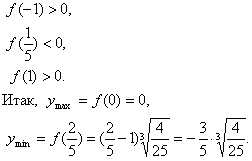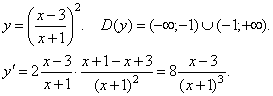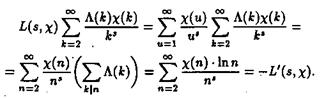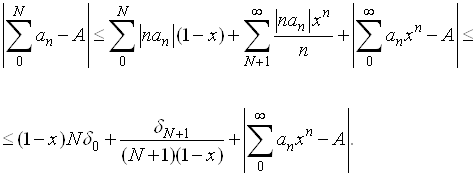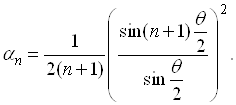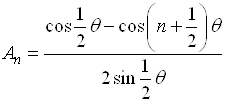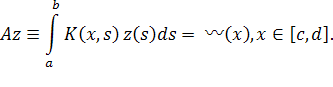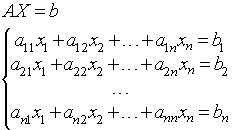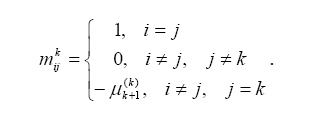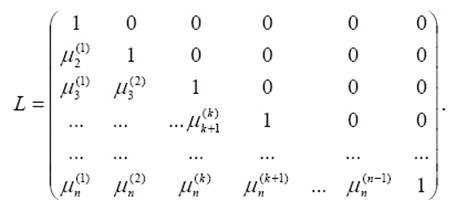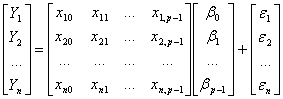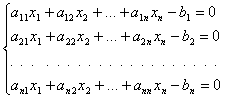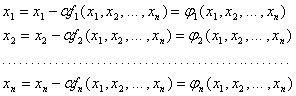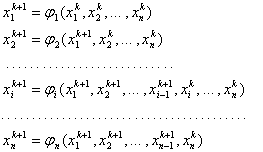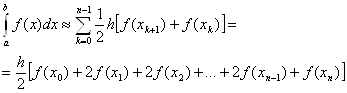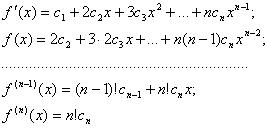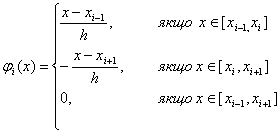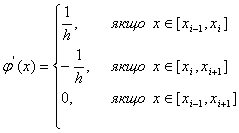| № | Название работы | Скачать |
|---|---|---|
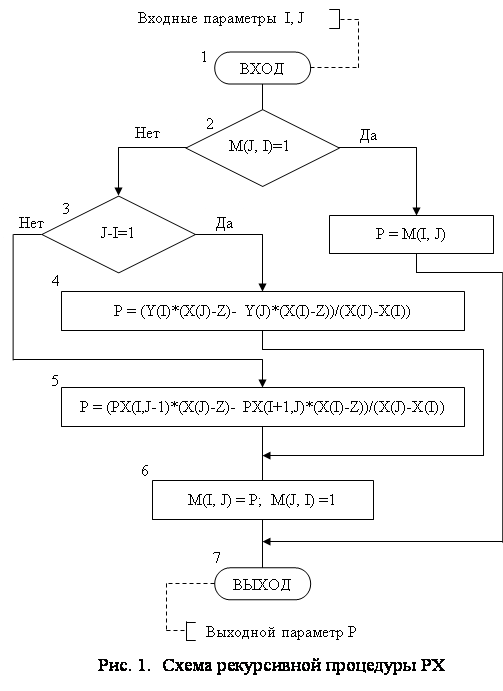
| 301. |
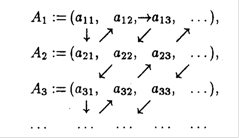
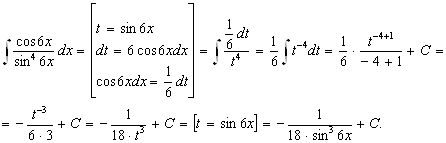
Некоторые интерполяционные свойства конечномерных сетевых пространств и пространств Лоренца ... Теорема доказана. Аналогичные задачи для интегральных операторов были рассмотрены в работах [1], [5]. 4. Некоторые интерполяционные свойства семейств конечномерных пространств Пусть 1 ≤ p < ∞, 1 ≤ q ≤ ∞. Определим семейство конечномерных пространств: ... |
|
| 302. |
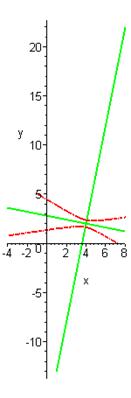
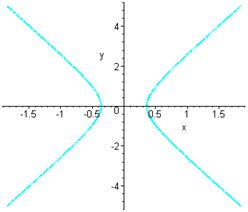
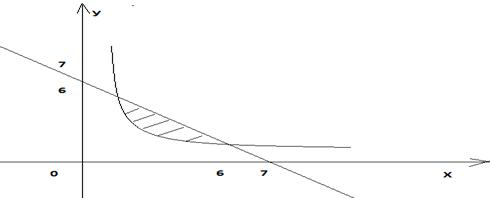
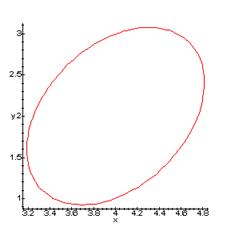
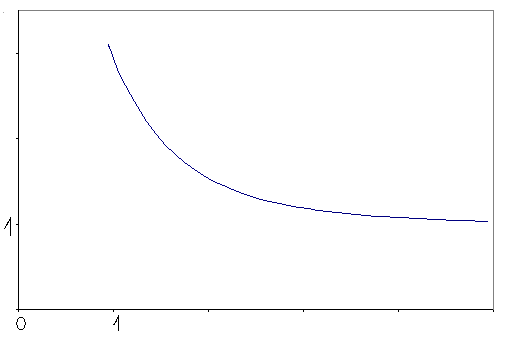
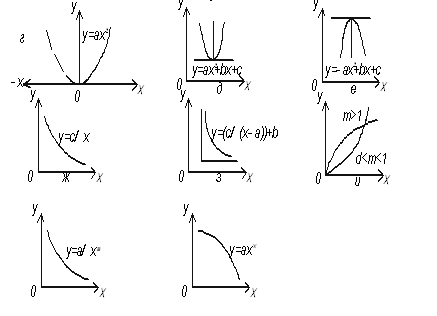
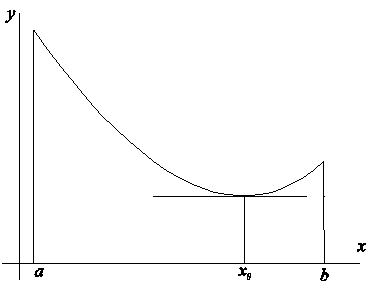
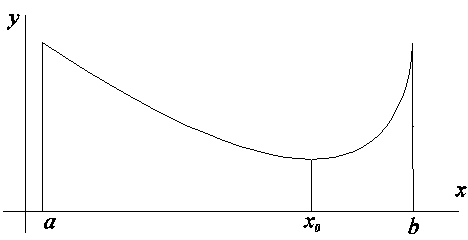
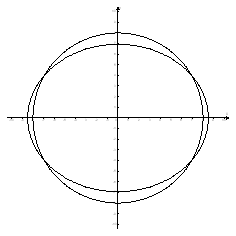
Геометрические свойства кривых второго порядка ... II. Переход от общего уравнения кривой к каноническому Рассмотрим теперь случай, когда, и исследуем данное уравнение кривой второго порядка с помощью инвариантов. Из вышеприведенной таблицы видим, что при уравнение (1) определяет гиперболу и принимает вид: (2.1) ... |
|
| 303. |
Вивчення систем, еквівалентних системам з відомим типом крапок спокою Застосування теореми про еквівалентність диференціальних систем Висновок Список джерел Введення У курсовій роботі розглядається вложима система з відомим типом крапок спокою. Як відомо система є вложимою, якщо будь-який компонент цієї системи вложима, тобто система вложима тоді й тільки ... |
|
| 304. |
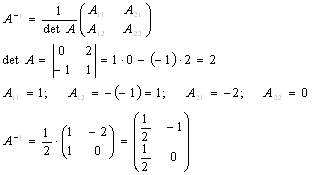
Аналитическая геометрия в решении экономических задач ... для обеспечения выпуска единицы конечного продукта j-й отрасли В соответствии с экономическим смыслом задачи значения должны быть неотрицательны при неотрицательных значениях Матрица называется продуктивной, если для любого вектора существует решение уравнение (2.19). В этом случае и модель ... |
|
| 305. |
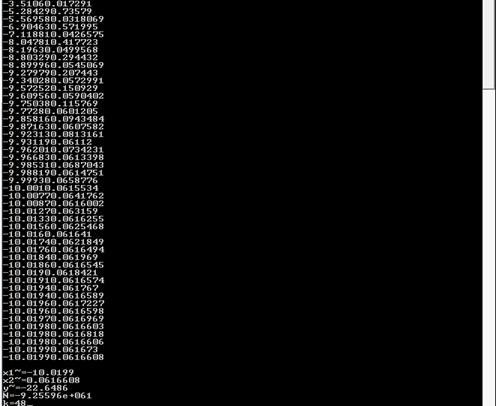
Застосування методу Монте-Карло для кратних інтегралів ... статистичних випробувань. Теорія методу Монте-Карло вивчає способи вибору випадкових величин для вирішення різних завдань, а також способи зменшення дисперсії випадкових величин. 3. Програма обчислення кратного інтеграла методом Монте-Карло Обчислити певний інтеграл . за методом “Монте-Карло” по ... |
|
| 306. |
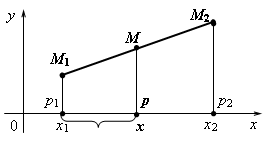
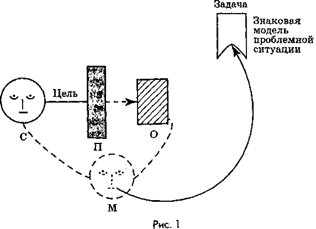
Дифференциальные уравнения ... , что С является функцией от y: Дифференцируя полученное, имеем: Но Откуда: Следовательно: Ответ: Задача 8. Для данного дифференциального уравнения методом изоклин построить интегральную кривую, проходящую через точку М. Решение: Чтобы решить ... |
|
| 307. |
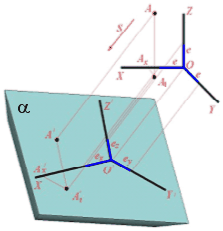
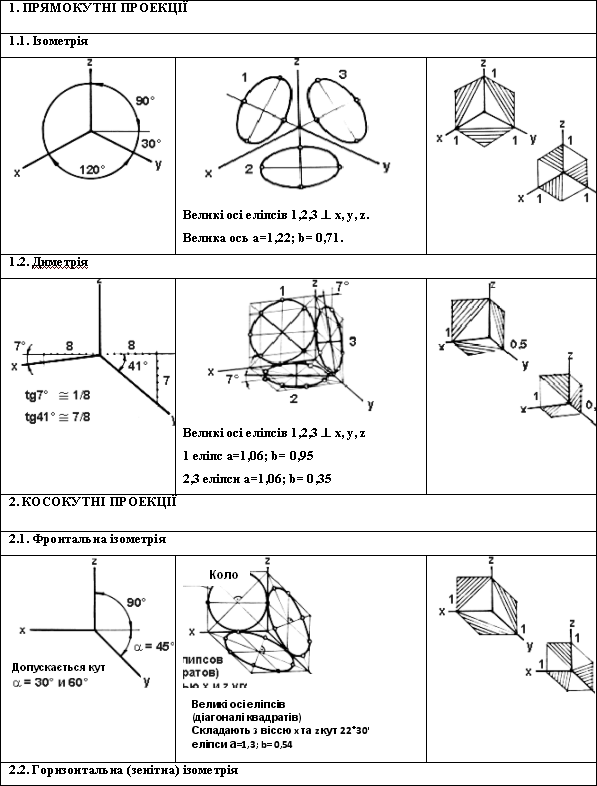
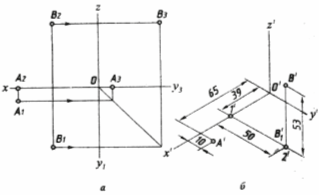
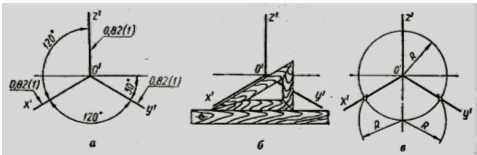
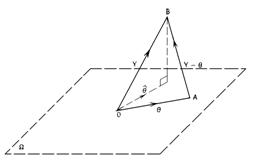
Аксонометричні проекції ... деякими величинами, їм пропорційними. Ці величини будемо називати приведеними коефіцієнтами спотворення. Відношення між аксонометричними проекціями відрізків, які паралельні осям координат X, Y, Z та самим відрізкам рівні коефіцієнтам KХ = еХ /e, KY = еY /e, KZ = eZ /e. Тому сутність ... |
|
| 308. |
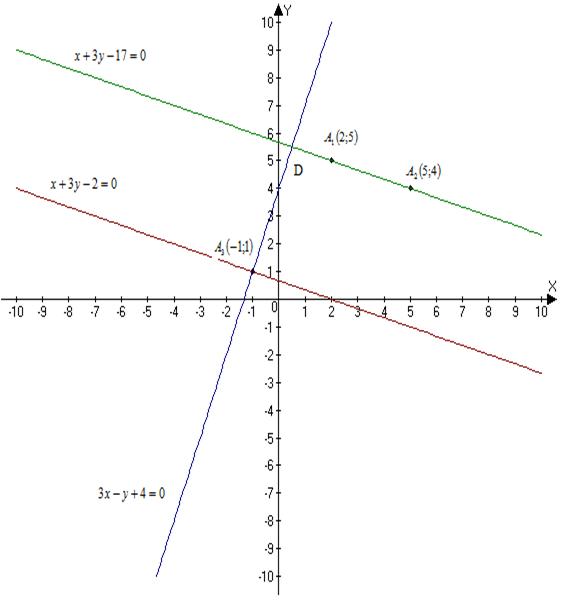
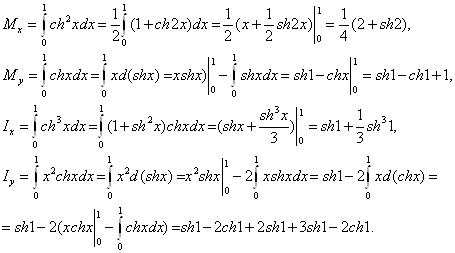
Системы линейных алгебраических уравнений ... определитель не равен 0, значит, система векторов линейно независима. Ответ: 1) ; 2) ; 3) ; 4) система векторов линейно независима. Задание №4 Даны координаты точек: Требуется: 1) найти общее уравнение прямой , проходящей через точки А1 и А2; 2) найти уравнение ... |
|
| 309. |
Українська математична термінологія: історія та сучасний стан ... медичної секції Наукового товариства імені Шевченка виходить стаття професора з Ростова-на-Дону Д. Мордухай-Болтов-ського «Про українську та білоруську математичну термінологію в зв'язку з історією російської». Автор зазначає, що при утворенні російської термінології систематичного колегіального обм ... |
|
| 310. |
Рішення ірраціональних рівнянь ... радикалами потрібне вміти користуватися кожним із цих методів і вибирати в кожному випадку оптимальний. 3. Не стандартні методи рішення ірраціональних рівнянь Існують ірраціональні рівняння, які вважаються для школярів звичайних освітніх шкіл задачами підвищених труднощів. Для рішення таких ... |
|
| 311. |
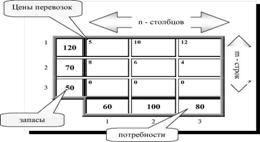
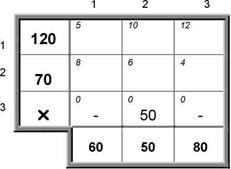
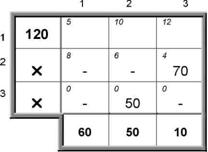
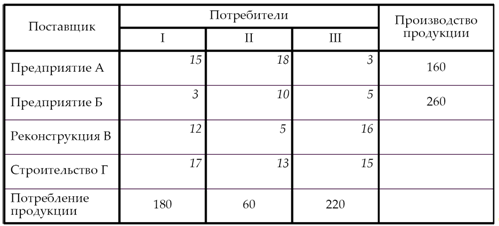
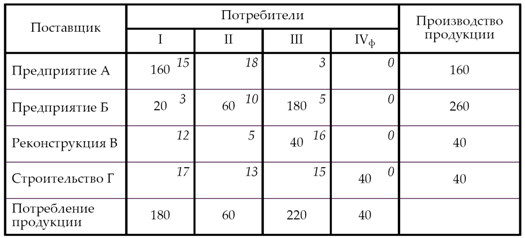
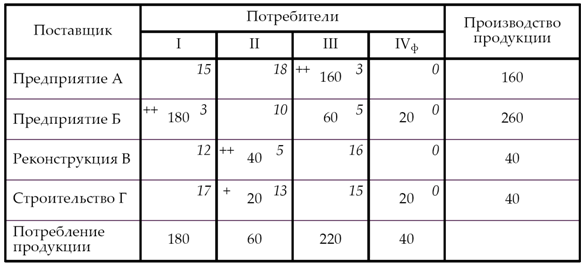
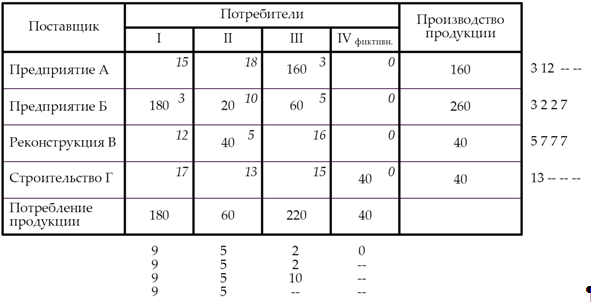
Решение транспортной задачи в Excel ... так, чтобы время выполнения работ было минимальным, а каждую работу выполнял только один рабочий. §4. Решение транспортной задачи в Excel В качестве примера я рассмотрел транспортную задачу для 2 складов и 5 магазинов. · В ячейки C4:C5 записал объемы продукции, имеющиеся на 2 складах. ... |
|
| 312. |
Решение задач линейного программирования в среде Maple ... равным некоторому числу (тоже, вообще говоря, любому). После этого оставшаяся система имеет единственное решение. §4. Пример решения задача линейного программирования Решим задачу линейного программирования симплекс – методом : f(x) = 2x1 + 3x2 + 4x3→ max 3x1 + x2 + 3x3<=5 ... |
|
| 313. |
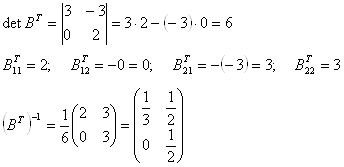
Основы высшей математики построить диаграммы Венна. С + АВ – ВТ А = C = A x B C11 = 2 x (-1) + (1 x 0) + 3 x 2 = -2 +6 = 4 C12 = 2 + 1 x1 +3 x 2 = 2+1 +6 = 9 C13 = 2 x 5 + 1 x 3 + 3 x 4 = 10 + 3 + 12 = 25 C21 = -1 x 1 + 3 x 0 + 3 x 2 = -1 + 6 = 5 C22 = 1 x 1+ 3 x1 +3 x 2 = 1 + 3 + 6 =10 C23 = 1 x 5 + 3 x 3+ ... |
|
| 314. |
Оптимизация организационных решений ... образом, устанавливаем, что есть два равноценных оптимальных варианта последовательности строительства объектов. Задание №4 Оптимизация очередности строительства объектов в неритмичных потоках Определить оптимальную очередность строительства нескольких объектов, при которой ... |
|
| 315. |
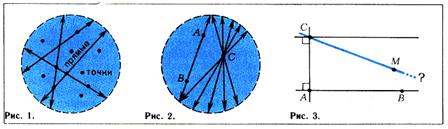
Предельные точки ... любого множества замкнуто. Теорема 4. Замыкание есть наименьшее замкнутое множество, содержащее . Пусть . Если к множеству добавить все его предельные точки, то получим множество, называемое замыканием и обозначим его так: . У замкнутого множества предельных точек, не принадлежащих ему, нет. ... |
|
| 316. |
Статистическая обработка результатов прямых многоразовых измерений с независимыми равноточными наблюдениями ... U(16)=170.35 U(32)=170.50 Доверительная вероятность: P= 0, 99 Доверительные границы: Разрядность: 5 разрядов* Количество наблюдений: n = 32 Обработка результатов измерений Анализируем серию наблюдений на наличие промахов. Если они имеются, то их необходимо исключить из ... |
|
| 317. |
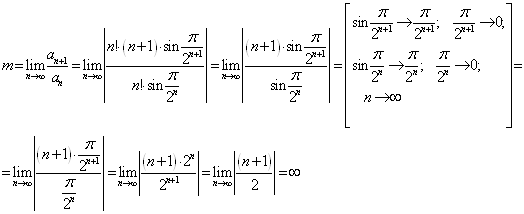
Основы математического анализа ... + 1 или n3 > 3n2 + 3n + 1. Учитывая неравенство (2n > n3), получим 2n+1 = 2n·2 = 2n + 2n > n3 + n3 > n3 + 3n2 + 3n + 1 = (n + 1)3. Таким образом, согласно методу математической индукции, для любого натурального n Î N, n ≥ 10 имеем 2n > n3. Пример 3. Доказать, что ... |
|
| 318. |
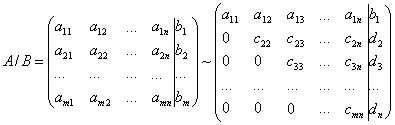
Системы линейных уравнений и неравенств ... вида, из которой последовательно, начиная с последних (по номеру) переменных, находятся все остальные переменные. Рассмотрим решение системы (1) m линейных уравнений с nпеременными в общем виде: (3) Если m=n, то рассмотрим расширенную матрицу. Учитывая правую часть, приведем данную матрицу ... |
|
| 319. |
Творчество Герона, Менелая и Птолемея ... . В отличие от образа Елены, восходящего к древнейшему растительному божеству, образ Менелая является плодом героического сказания, возможно, опирающегося на какие-то исторические воспоминания микенской эпохи. О месте Птолемея в истории науки Клавдий Птолемей занимает одно из самых почетных мест в ... |
|
| 320. |
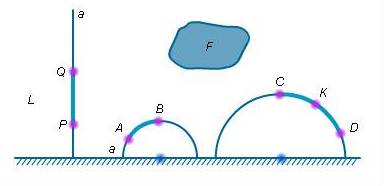
Геометрические построения на местности с помощью циркуля и короткой градуированной веревки ... . Гипотеза: мы предполагаем, что сможем решить некоторые геометрические задачи на построение, используя не классический набор инструментов (циркуль и линейку), а набор из циркуля и короткой градуированной веревки. Задачи о построении на местности Геометрия зародилась в глубокой древности, она ... |
|
| 321. |
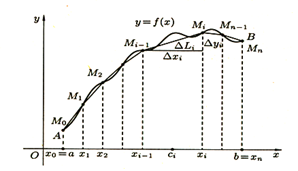
Интерполирование функций ходной функции f(x) для значений аргумента x, отличных от узлов интерполяции. Такая операция называется интерполированием функции f(x). При этом различают интерполирование в узком смысле, когда x принадлежит интервалу [x0, xn], и экстраполирование, когда x не принадлежит этому интервалу. В такой ... |
|
| 322. |
Лист Мебиуса ... (поверхность допускающая ориентацию) с краем. Лист Мёбиуса — это также пространство нетривального расслоения над окружностью с слоем отрезок. Лист Мёбиуса — двухмерное компактное множество (т.е. поверхность) с границей. Это стандартный пример поверхности, которая не ориентируема. Лист Мёбиуса — ... |
|
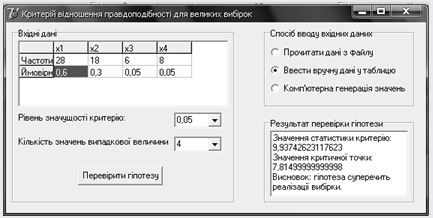
| 323. |
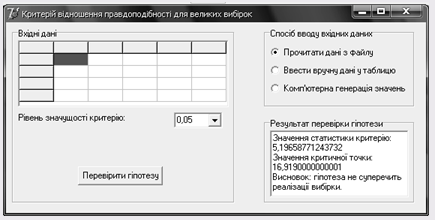
Критерій відношення правдоподібності для великих вибірок ... Звідси, Тут,. Тому статистика критерію матиме вигляд: . У наступному розділі ми більш детально розглянемо застосування критерію відношення правдоподібності для великих вибірок до перевірки статистичних гіпотез. 3. Приклади застосування критерію відношення правдоподібності для ... |
|
| 324. |
Діафантові рівняння ... 0. 𝑥=0, 𝑥=2. при 𝑦=2, 𝑥=1, 𝑥=2. Відповідь: (0, 0), (0, 1), (1, 0), (1, 2), (2, 1), (2, 2). Приклад 4. Знайти всі розв’язки рівняння в цілих числах: Розв'язок. Нехай , де 𝑥, 𝑦, 𝑧 – цілі числа. ... |
|
| 325. |
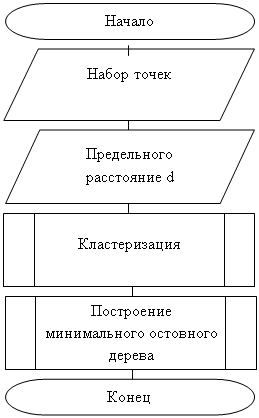
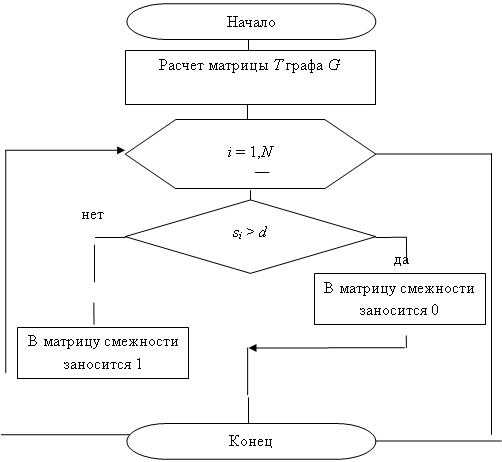
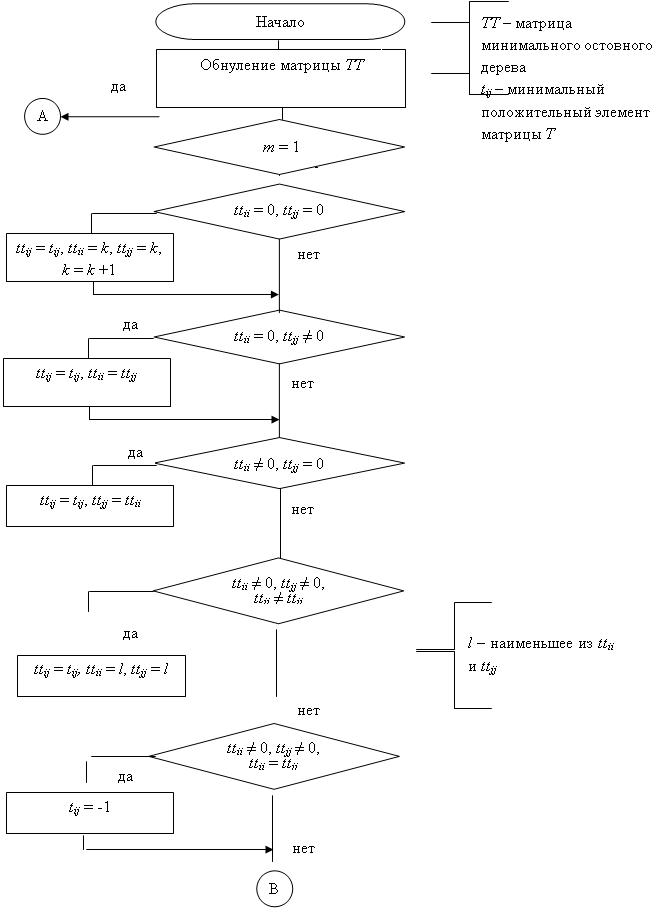
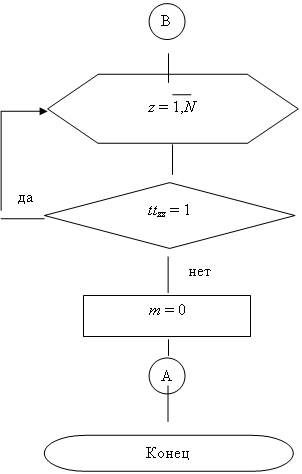
Двумерная кластеризая по предельному расстоянию. Дискретная математика ... 7. Рисунок 7 – Тест первый (часть 3) 4.1 Тест второй. Результат выполнения алгоритма с 20-ю вершинами, заданными случайными координатами и предельным расстоянием равным 2,5 представлен на рисунке 8. Рисунок 8 – Тест второй (часть 1) На данном рисунке видно, что граф был разбит ... |
|
| 326. |
Двойные интегралы и дифференциальные уравнения второго порядка ка» Тема: «ДВОИНЫЕ ИНТЕГРАЛЫ И ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ВТОРОГО ПОРЯДКА» УК (220501.65)/3. сокращенная Выполнил студент Петренко Н. В.Нижневартовск 2010 Контрольная работа Вариант 5 1. Вычислить интегралы: 1.1. где D – прямоугольник 1.2. ... |
|
| 327. |
Градієнтні методи ... . Крок 4. Якщо ||||£e3, то пошук точки мінімуму закінчується й покладається: Інакше до=до+1 і перехід до кроку 2. 1.5 Методи ярів 1.5.1 Загальна характеристика Градієнтні методи повільно сходяться в тих випадках, коли поверхні рівня цільової функції f (x) сильно витягнуті. Цей ... |
|
| 328. |
Гипергеометрическое уравнение ... для вырожденной гипергеометрической функции и его интегралы, представление различных функций через вырожденные гипергеометрические функции. 1. Гипергеометрическое уравнение 1.1 Определение гипергеометрического ряда Гипергеометрическим рядом называется степенной ряд вида , где z – ... |
|
| 329. |
Вычисление интегралов ... (слоя), – площадь его основания, т.е. dv = . Таким образом, dр = . и 3) Интегрируя полученное равенство в пределах от х = 0 до х = Н, находим A 8. Вычисление интегралов с помощью пакета MathCAD При решении некоторых прикладных задач требуется использовать операцию символического ... |
|
| 330. |
Роль простых чисел в математике ... . Но они не умели этого доказывать. Пифагор или кто-то из его последователей нашел доказательство этого утверждения. Теперь легко объяснить роль простых чисел в математике: они являются теми кирпичиками, из которых с помощью умножения строят все остальные числа. Хорошо было бы, если все простые ... |
|
| 331. |
Расчет математического ожидания и дисперсии ... по формуле Байеса: ()= = Ответ: 0,62 5. Бросаются две игральные кости. Найти для произведения очков на выпавших гранях: математическое ожидание; дисперсию Решение. Введем независимые случайные величины и равные, соответственно, числу очков, выпавших на первой и на второй ... |
|
| 332. |
Проблема Ферма для простых показателей больше 3 ... противоречию: левые части (1.44) и (1.45) делятся на K 2, а правые их части не делятся на K 2. Проблема Ферма (первый и второй случаи) для всех простых показателей Р = 6n + 1 доказана. 1.7 Второй случай ПФ для простых показателей вида 6n + 5 В это разделе в качестве модулей будем ... |
|
| 333. |
Теория вероятностей и математическая статистика ... сумме будет 15 очков при 5 бросаниях, если бросается монета в 3 копейки} = {при 5 бросаниях 5 решек} n = 5 p = 1/2 - вероятность выпадения решки q = 1 - p = 1/2 m - количество бросаний, при которых выпадет решка P(A Р1 = З(ь=3) = С(3ж5)*((1.2):3)*((1.2):2) = 10*(1.8)*(1.4) = 10.32 =0ю3125 З(Ф/Р2) ... |
|
| 334. |
Математические последовательности. Предел функции ... при выполняется неравенство . Используя определение предела последовательности, докажем, что . Возьмем любое число . Если взять , то для всех будет выполняться неравенство . Следовательно, . Доказано Задание 3 Пользуясь определением предела функции, докажите, что . Доказательство ... |
|
| 335. |
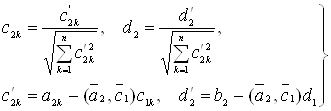
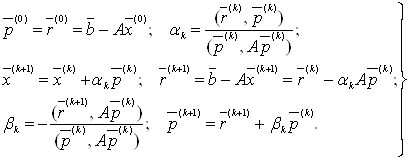
Дослідження методу ортогоналізації й методу сполучених градієнтів ... значення. З новими наближеними значеннями надходять точно також і т.д. Розглянемо два точних методи: метод ортогоналізації й метод сполучених градієнтів. 1. Метод ортогоналізації 1.1 Метод ортогоналізації у випадку симетричної матриці Нехай дана система (1) порядку n. Щоб ... |
|
| 336. |
Дослідження локальних формацій із заданими властивостями ... дформація формації має внутрішній локальний - екран. Зокрема, будь - яка локальна підформація формації має внутрішній локальний - екран. Локальні формації із заданими властивостями Нехай – деяка операція, – локальний екран формації . Природно виникають два питання: 1) чи Буде - замкнутої, ... |
|
| 337. |
Дослідження кривої й форми поверхні другого порядку ... вши його до канонічного виду, ми встановили, що дана крива — еліпс. Ми одержали канонічне рівняння гіперболи за допомогою перетворень паралельного переносу й повороту координатних осей. Дослідження форми поверхні другого порядку Теоретична частина Поверхнею другого порядку S назива ... |
|
| 338. |
Дослідження дзета-функції Римана ... представляє випадок викладений у другому розділі. Розділ 2 Всі результати першого розділу, що стосуються дзета-функції Римана, були отримані в припущенні, що її аргумент s – дійсне число. Однак, найвидатніші дослідження й численні важливі додатки стали можливі лише після включення в область ... |
|
| 339. |
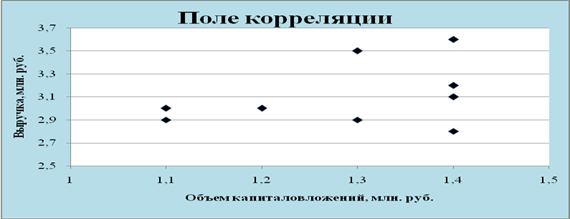
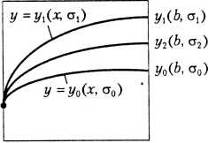
Визначення емпіричних закономірностей ... значення; - вирівняні значення. Застосуємо цей метод для визначення параметрів функціональних залежностей. а) Нехай між даними прямопропорційна залежність, тобто теоретична крива, за допомогою якої будемо вирівнювати емпіричну залежність між цими величинами має такий вигляд: (7) Тоді ... |
|
| 340. |
Беселеві функції ... , треба, що . Використовуючи (11), одержимо: ; ; . По членне додавання й вирахування отриманих рівностей дає: , (12) . (13) Формула (13) дозволяє виразити всі Беселеві функції із цілими індексами через , . Дійсно, з (13) знаходимо (думаючи ): , (13`) звідки послідовно одержу ... |
|
| 341. |
Аналіз експериментальних даних ... , Як аналітична залежність підібрана, необхідно математичними перетвореннями привести її до рівняння прямої лінії, тобто перетворити вихідні дані і обчислити значення параметрів, які входять в аналітичну залежність. Приведення криволінійної залежності до рівняння прямої лінії дозволяє використати ... |
|
| 342. |
Факторизації чотирьохмірних симплектичних груп ... ми будемо розуміти довільну підгрупу з . Група , одержувана із застосуванням гомоморфізму , називається проективної симплектичною групою знакозмінного простору . Під проективною групою симплектичних перетворень простору будемо розуміти будь-яку підгрупу групи . Пропозиція 29 Якщо - ненульовий ... |
|
| 343. |
Типовой расчет ицы несложно найти общее число равновозможных исходов испытания: n = 36; и число исходов, благоприятствующих появлению события В: m = 7. В результате получаем: Таким образом, искомая вероятность равна 0,1944. Ответ: а) 1; б) 0,6389, в) 0,1944. 2. Имеются n изделий 4-х сортов, причём , где ... |
|
| 344. |
Типовой расчет мму ряда: Решение. Разложим дробь , используя метод неопределённых коэффициентов. то есть: , , , Следовательно, Тогда, исходный ряд примет вид: Найдём n – первых членов ряда , записывая дроби с одинаковыми знаменателями, друг под другом: = = = = ... |
|
| 345. |
Элементы математической статистики ... значимости , - для уровня значимости , -число степеней свободы. 1.2 Наиболее важные распределения, применяемые в математической статистике 1.2.1 Нормальное распределение Случайная величина , распределенная по нормальному закону, описывается плотностью вероятности: . ... |
|
| 346. |
Середні значення та їх оцінки ... середньому затрачають 11 хв. Середня квадратична для величин х1, х2. .....хn від їх середнього значення х. Середня квадратична незважена буде: (3) Середня квадратична зважена — (4) Середню квадратичну використовують тоді, коли варіанти є відхиленням фактичних величин від їх середньої ... |
|
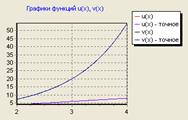
| 347. |
Рішення систем диференціальних рівнянь за допомогою неявної схеми Адамса 3-го порядку ... . Як тестова задача була вирішена задача Коші за допомогою неявної схеми Адамса 3-го порядки на інтервалі [2,4] з початковими умовами : . Точним рішенням даної системи є функції: Було потрібно домогтися рішення системи диференціальних рівнянь із точністю до 0.0001. Результат рішення ... |
|
| 348. |
Рішення лінійних рівнянь першого порядку ... виглядати в такий спосіб: Вирішуємо систему 16-го порядку з рівняння A*S = S*В Знаходимо деякі елементи й одержуємо наступну матрицю S: Зробимо перевірку A*S - S*В=0: Значить матриця переходу знайдена вірно. Для знаходження вектора рішень y необхідно помножити матрицю S ... |
|
| 349. |
Разложение функций. Теория вероятностей ... коэффициенты вычисляются: Замечание: в случае разложения функции f(x) в ряд Фурье в произвольном интервале (a; a+2l) длины 2l пределы интегрирования в формулах (2), у коэффициентов Фурье нужно заменить соответственно на (а) и (a+2l). Теория вероятностей Основным понятием в теории ... |
|
| 350. |
Проверка больших чисел на простоту их чисел на простоту. Метод Ферма. Цель: Изучить методы генерации и проверки на простоту больших чисел. Ход работы: Листинг программы: Program.cs using System; using System.Collections.Generic; using System.Linq; using System.Text; namespace Tania_KMZILab3 { classProgram { ... |
|
| 351. |
Основные понятия математического анализа повторный по формуле: Сначала вычисляется внутренний интеграл, затем внешний. При вычислении внутреннего интеграла ‘х’ считается переменной, а ‘у’-постоянной. 3. Если область интегрирования не относится ни к 1 ни ко второму случаю, то разбиваем ее на части таким образом, чтобы каждая из ... |
|
| 352. |
Проценты и их применение ...
100 а = 4,04% ОТВЕТ: через каждый полгода зарплату сотрудникам надо поднимать на 4,04% 4. Применение процентов в жизни 4.1 Исследование бюджета семьи Проценты широко применяются в повседневной жизни. Я покажу это на примере бюджета моей семьи. Порядковый номер члены ... |
|
| 353. |
Пространства Соболева ... и неравенства Фридрихса. Следствие 2. В нормы (1.9) и (1.10) эквивалентны. Действительно, используя неравенство Фридрихса, имеем 2. Применение пространств Соболева в математической физике 2.1 Доказательство существования и единственности обобщённого решения уравнения Лапласа ... |
|
| 354. |
Производная, дифференциал и интеграл ... . Для ее раскрытия разложим числитель и знаменатель на множители и сократим на общий множитель , который при не равен нулю. В результате неопределенность будет раскрыта. 2. Производная и дифференциал Пусть функция определена в некоторой окрестности точки . Производной функции в точке ... |
|
| 355. |
Применение численных методов для решения уравнений с частными производными ... = 1.0178 -0.4243 0.0718 coef2 = 0.0718 -0.4243 1.0178 delt2 = 0.1199 delt2 = 0.0719 Численные методы решения задачи Коши для обыкновенных дифференциальных уравнений Эйлера явная function dy=func(x,y) dy=2*x*y clear X=[0.00000 0.10000 0.20000 0.30000 0.40000 0.50000]; Y= ... |
|
| 356. |
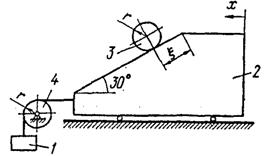
Применение уравнение Лагранжа II рода к исследованию движения механической системы с двумя степенями свободы ... производные в уравнения Лагранжа (11): или (j=1,2,…, s). (12) Уравнения (12) называются уравнениями Лагранжа второго рода для консервативной системы. 7 Применение уравнений Лагранжа II рода к исследованию движения механической системы Массы тел механической системы m= 2m; ... |
|
| 357. |
Применение ТСО в математике ... довольно простой переделкой в кодоскоп школьного эпидиаскопа. Более подробно о дидактических возможностях кодоскопа говорится в статье "Применение кодоскопа па уроках математики" Там, где нужно продемонстрировать некоторое математическое свойство в динамике, в процессе изменения ... |
|
| 358. |
Применение тригонометрической подстановки для решения алгебраических задач ... работы. 5. Анализ полученных результатов опытной работы. Этап 1. Разработка факультативного курса на тему: «Применение тригонометрической подстановки для решения алгебраических задач» » с учащимися классов с углубленным изучением математики. Факультативный курс был разработан на основе ... |
|
| 359. |
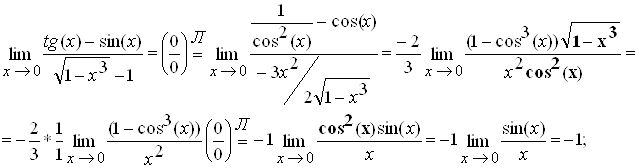
Применение производной при нахождении предела ... и последующего раздела были взяты из [Марон]. В четвертом разделе приведен вывод формулы Тейлора и показано применение формулы Тейлора для нахождения эквивалентных функций и вычисления пределов. 1. Бесконечно малые и их сравнения; символы "o малое" и "о большое" ... |
|
| 360. |
Применение производной и интеграла для решения уравнений и неравенств ... [1;+¥). Отсюда получаем, что f(1)=–1 будет наибольшим значением функции, так что для x>0 выполняется
ln x £ x-1. 1.3. Применение производной при решении уравнений Покажем, как с помощью производной можно решать вопросы существова-ния корней уравнения, а в некоторых случаях ... |
|
| 361. |
Приложения определенного интеграла к решению некоторых задач механики и физики ... равна па. По теореме Гульдена имеем Отсюда , т.е. центр масс C имеет координаты C. 2. Физические задачи. Некоторые применения определенного интеграла при решении физических задач иллюстрируются ниже в примерах 4—7. Пример 4. Скорость прямолинейного движения тела выражается формулой (м/с). ... |
|
| 362. |
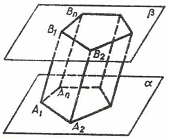
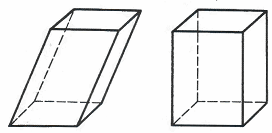
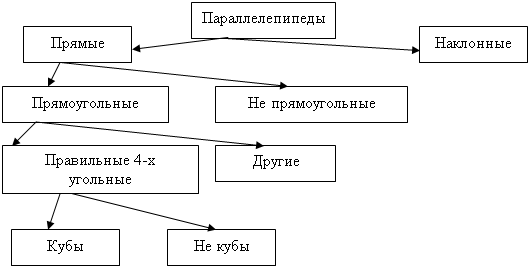
Призма и параллелепипед ... 12 24 6 3. Многогранник, составленный из двух равных многоугольников и , расположенных в параллельных плоскостях, и n параллелограммов …, , называется: А) параллелепипед; Б) призма; В) пирамида; Г) многогранник; Д) конус. 4. Перпендикуляр, проведенный из какой-нибудь точки одного ... |
|
| 363. |
Преследование на плоскости ... , если бы его скорость была хотя бы немного больше он бы убежал. Найти отношение скорости лис и скорости кролика. 4. Преследование на плоскости с одним преследователем В данной игре существует оптимальная стратегия и для преследователя и для убегающего игрока. Оптимальной стратегией для ... |
|
| 364. |
Представления конечных групп ... к , где , а – величина, комплексно – сопряженная к . В этом параграфе мы покажем, что каждое представление конечной группы эквивалентно некоторому ее унитарному представлению и является мполне приводимым. Матрица называется эрмитовой, если , и положительно определенной, если для каждого ... |
|
| 365. |
Построение прямоугольной системы координат ... . В I и III семестрах предусмотрен экзамен, во II и IV семестрах – зачет. 3-ий учебный вопрос ПРЯМОУГОЛЬНАЯ СИСТЕМА КООРДИНАТ. ПОЛЯРНЫЕ КООРДИНАТЫ И ИХ СВЯЗЬ СПРЯМОУГОЛЬНЫМИ Прямоугольная система координат на плоскости вводится следующим образом. Возьмем на плоскости две взаимно ... |
|
| 366. |
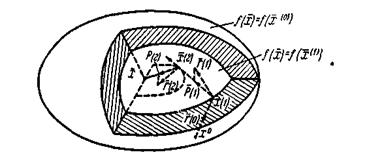
Построение математической модели оптимального управления, обеспечивающего мягкую посадку при минимальном расходе топлива ... расход топлива меньше. Получить программу оптимального управления, когда до некоторого момента t1 управление отсутствует u*=0, а начиная с t=t1, управление равно своему максимальному значению u*=umax, что соответствует минимальному расходу топлива. 6.) Решить каноническую систему уравнений, ... |
|
| 367. |
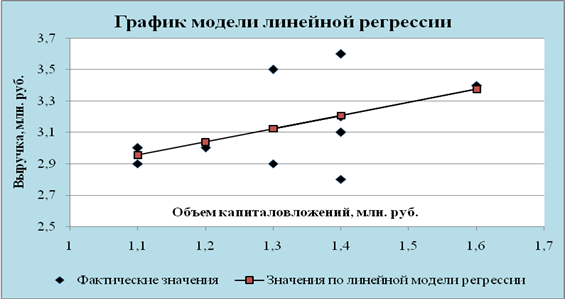
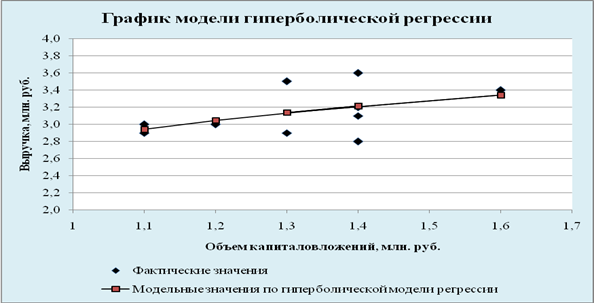
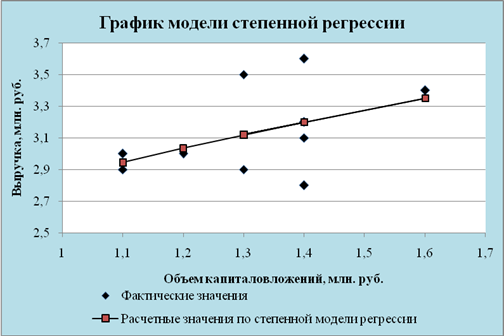
Построение математических моделей ... детерминации, F – критерия Фишера и меньшее значение средней относительной ошибки аппроксимации имеет линейная модель. Т.е. она лучше и точнее из всех построенных моделей описывает зависимость выручки от объема капиталовложений. Ее можно взять в качестве лучшей для построения прогноза. 11. ... |
|
| 368. |
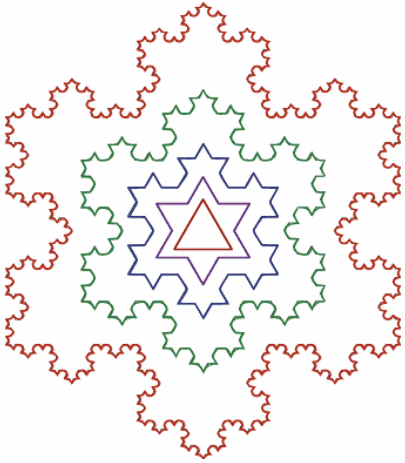
Поняття фракталів ... і інші геометричні фігури, без яких людині не можливо розібрати жодного її слова; без них вона подібна блукаючому в пітьмі…” Поняття фрактала змінило багато традиційних уявлень про геометрію, а в історії розвитку математики введення цього поняття стало переломним моментом. З кожним роком поняття ... |
|
| 369. |
Операции на графах ... компоненты из Y. Рассмотрим группу вершин результирующего графа, которые имеют общую компоненту x1: z1=(x1y1), z2=(x1y1), z3=(x1y3). Согласно определению операции декартова произведения графов, множество дуг между этими вершинами определяется связями между вершинами множества Y. Таким образом, дуга ... |
|
| 370. |
Операторы проектирования ... функций на отрезке [0, 2p]. Норма в нем определяется = Определение. Пусть X, Y – два топологических линейных пространства. Линейным оператором, действующим из X в Y, называется отображение y = Ax, где x принадлежит X, а y принадлежит Y, удовлетворяющее условию A(ax+bx) = aAx+bAx. Определение. ... |
|
| 371. |
Операторные уравнения ... , кто занимается приложениями математики. Поэтому данная работа разделена на две главы, в первой содержатся необходимые теоретические обоснования способов решения операторных уравнений и суть обоих методов, а во второй – решения конкретных задач. Глава 1. Операторные уравнения §1.Определение ... |
|
| 372. |
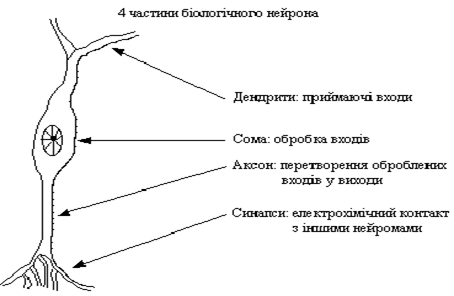
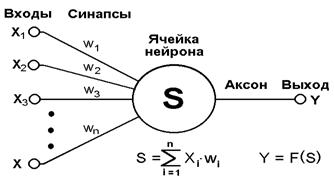
Нейронные сети ... , однако фактически оно ограничено ресурсами компьютера или специализированной микросхемы, на которых обычно реализуется нейросеть. Чем сложнее нейронная сеть, тем масштабнее задачи, подвластные ей. Выбор структуры нейросети осуществляется в соответствии с особенностями и сложностью задачи. Для ... |
|
| 373. |
Неединственность преобразований Лоренца. ... (2) формулы (1), тогда (в трехмерном пространстве, на котором заданы координаты T,X,Y): (3) T= AT’+BX’, X= DT’+EX’, Y=Y’, уравнения (3) в точности совпадают с известными преобразованиями Лоренца, а значит ортогональны. Ч.т.д. Но мы видим, что при введении произвольного коэффициента N для всех ... |
|
| 374. |
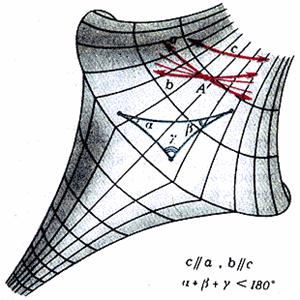
Неевклидова геометрия ... , например, для решения псевдосферических треугольников. Псевдосферу, которую мы назвали «моделью», Бельтрами назвал интерпретацией (истолкованием) неевклидовой геометрии на плоскости. Впоследствии, с развитием и введением в математику аксиоматического метода, под Рисунок 4 интерпретацией (или ... |
|
| 375. |
Этапы изучения понятия задачи и её решения в начальных класах ... », решение составных задач. Предшествует этому особая подготовительная работа. Заключение В курсовой работе обозначены этапы изучения понятия задачи и её решения в начальных классах, раскрыто их содержание. Дана методико-математическая характеристика основных понятий исследования таких как ... |
|
| 376. |
Эрмитовы операторы ... ;1 и λ2, ортогональны. Действительно, из соотношений Lu1 = λ1 и1, Lu2 = λ2и2, из вещественности λ1 и λ2 и из эрмитовости оператора L получаем цепочку равенств λ1(и1,и2) = (λ и1,и2) = (Lи1,и2) = (и1,Lu2) = (и1,λ2и2) = =λ2(и1,и2), т.е. &# ... |
|
| 377. |
Элементы алгебры и геометрии 8729; (-2) ∙ 3 + 1 ∙ 1 ∙ 0 – 3 ∙ 4 ∙ 1 – 1 ∙ 3 ∙ 6 – 2 ∙ 0 ∙ (-2) = = 48 – 18 + 0 – 12 -18 – 0 = 0 Δ3 = = = 2 ∙ 1 ∙ 0 + (-3) 4 ∙ 3 + 3 ∙ 1 ∙(-2) – 3 ∙1 ∙ 3 – 1 ∙ (-3) ∙ 0 – 2 ∙ ... |
|
| 378. |
Элементарное изложение отдельных фрагментов теории подгрупповых функторов ... ) Если и - нормальные подгруппы группы , причем , то изоморфна . Лемма 3.1 Пусть - формация, . Тогда Лемма 20.6. Пусть - подгрупповой функтор и - группа. Если и , тогда . Лемма 20.7. Пусть , - элементарно абелевы -группы с . Тогда имеет подгруппу такую, что . Теорема. Пусть - такой ... |
|
| 379. |
Элементарное доказательство великой теоремы Ферма ... имеет целочисленных решений. Поэтому далее достаточно доказать, что целочисленных решений не имеет также и уравнение (14). Доказательство великой теоремы ферма. Уравнения (1) и (14) полностью эквивалентны, т.е. либо не существует целочисленных решений у обоих уравнений, либо целочисленные решения ... |
|
| 380. |
Экстремумы функции ... № 12записано в виде определителя), получаем Тогда, еслиимеет в т. условный максимум, если> 0 — то условный минимум. Пример: Найти точки экстремума функции если уравнение связи у - х = 0. Рассмотрим оба способа решения. 1. Из аналитической геометрии известно, что любое уравнение 2-го порядка ... |
|
| 381. |
Теорема Ферма. Бесконечный спуск для нечетных показателей n м Эйлер) доказывали эту теорему для частного случая n = 4 способом бесконечного спуска с помощью формул древних индусов: x= a- b, y=2ab, z= a+ b. Другие формулы: x = + b, y = + a, z = + a + b (1). В (1) a и b любые взаимно простые положительные целые числа, одно из них – чётное, другое ... |
|
| 382. |
Теорема Дирихле ... L (S,c)¹0/ Этим завершается доказательство теоремы По следствию 2 леммы 2 функция является аналитической в области ReS > 1. Для дальнейшего доказательства теоремы Дирихле нам будет необходимо представление этой функции в виде ряда, аналогичного ряда (2.16). Лемма. Для каждого характера ... |
|
| 383. |
Теорема Гурвица и ее приложение ... двойки, на которую делится число n. Разделим на 4 с остатком. Обозначим через a неполное частное, а через b остаток. Тогда =4a+b, . Число p равно [5] 6. Приложение теоремы Гурвица В 1878 г. Немецкий математик Г. Фробениус доказал следующую замечательную теорему. Теорема Фробениуса. Любая ... |
|
| 384. |
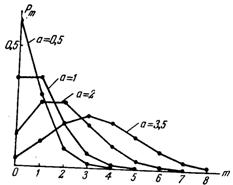
Теорема Бернулли. Закон распределения Пуассона. Критерий Колмогорова ... . Задание 2,3. Моделирование дискретной случайной величины, имеющей закон распределения Пуассона. Подтверждение гипотезы о том, что полученная случайная величина имеет данный закон распределения с помощью критерия Колмогорова. Закон Пуассона Рассмотрим случайную величину X, которая может ... |
|
| 385. |
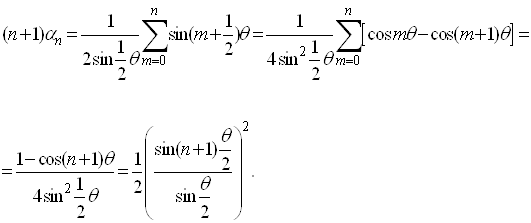
Суммирование расходящихся рядов ... Различные факты из области математического анализа, как, например, расходимость, произведения двух сходящихся рядов, естественно выдвинули вышеупомянутый вопрос: “О возможности суммирования расходящихся рядов, в некоем новом смысле”. Нужно сказать, что до создания Коши строгой теории пределов ... |
|
| 386. |
Эйлеровы графы ... обхода у данного графа, а именно граф должен быть связным и каждая его вершина должна быть инцидентна чётному числу рёбер.[6] Эйлеровы графы Решение Эйлером задачи о Кёнигсбергских мостах привела к первой опубликованной работе по теории графов. Задачу об обходе мостов можно ... |
|
| 387. |
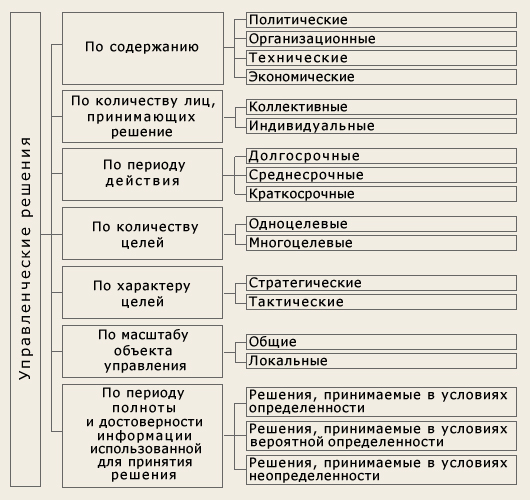
Структуризация задач принятия решений в условиях определенности. Некорректно поставленные задачи. Регуляризирующие (робастные) алгоритмы: адаптивные, инвариантные ... пространство U. В 1963 г. А.Н.Тихонов дал знаменитое определение регуляризирующего алгоритма (РА), которое лежит в основе современной теории некорректно поставленных задач. Определение. Регуляризирующим алгоритмом (регуляризирующим оператором) называется оператор, обладающий двумя следующими ... |
|
| 388. |
Шафаревич Игорь Ростиславович - российский математик ... пути ученого; 2) изучить и оценить спорные моменты в его работах; 3) выявить основные положения методологии И. Шафаревича. Глава 1. Биография И. Р. Шафаревича Шафаревич Игорь Ростиславович родился 3 июня 1923 г. в Житомире. Как пишет о себе сам Игорь Ростиславович в автобиографии, ... |
|
| 389. |
Стійкість системи лінійних алгебраїчних рівнянь ... і відносно l і, отже, як доводиться в алгебрі, має щонайменше один дійсний або комплексний корінь. Нехай l1 l2,… lm(m£n) — різні корені рівняння (5). Ці корені називаються власними значеннями, або характеристичними числами, матриці А, а сукупність всіх власних значень називається спектром ... |
|
| 390. |
Степінь з ірраціональним показником ... який маєть степені із від'ємним раціональним показником: та . Означення поняття А тепер дамо означення степеня з ірраціональним показником: Означення Степенем з ірраціональним показником та основою а, де а>0, називається дійсне число , яке є границею послідовності , де - послі ... |
|
| 391. |
Числовые ряды ... . Как указывалось в разделе 2, условно сходящиеся ряды таким свойством не обладают. Вопросы для самопроверки 1. Как определяется сумма числового ряда? 2. Какой ряд называется сходящимся (расходящимся)? 3. Может ли предел общего члена сходящегося числового ряда равняться 3? 4. Что можно ... |
|
| 392. |
Степенные ряды ... быть получен почленным интегрированием ряда (1.2), т. е. для всех . Следует отметить, что при почленном дифференцировании и интегрировании степенного ряда его радиус сходимости R не меняется, однако его сходимость на концах интервала может измениться. Приведенные свойства справедливы ... |
|
| 393. |
Численные методы решения типовых математических задач ... линейных алгебраических уравнений, используя метод простой итерации. 1.2 Математическая формулировка задачи Пусть А – невырожденная матрица и нужно решить систему где диагональные элементы матрицы А ненулевые. 1.3 Обзор существующих численных методов решения задачи Метод ... |
|
| 394. |
Статистичний аналіз тенденцій захворюваності в Україні ... що належать до п’ятої групи 6. м.Севастополь Рис 3.2.11 Область, що належать до шестої групи 3.3 Порівняння тенденцій росту захворюваності на СНІД серед областей України, А.Р.Крим, м. Київ та Севастополь I. Спочатку за критерієм паралельності прямих проводилась перевірка на паралельні ... |
|
| 395. |
Численные методы для решения нелинейных уравнений ... приближения (4) строятся по формулам: , (9) где – начальное приближение к точному решению . 4.5 Метод Зейделя на основе линеаризованного уравнения Итерационная формула для построения приближенного решения нелинейного уравнения (2) на основе линеаризованного уравнения (7) имеет вид ... |
|
| 396. |
Численные методы вычисления интегралов ... интеграла. При этом способе подынтегральную функцию приближают снизу и сверху интегрируемыми в замкнутом виде функциями и , т.е. , (34) Тогда (35) 5. Вычисление интегралов методом Монте-Карло Пусть нам нужно вычислить интеграл: (36) В случае, когда методы Ньютона-Котеса и ... |
|
| 397. |
Числа "е" та "пі" ... ( 15501617) [22], однак це необґрунтовано, тому що немає твердих підстав для твердження, що Непер мав про число е чітке позначення. Уперше математично обгрунтоване позначення числа "е" увів Леонард Ойлер (17071783). Він також обчислив точні 23 десяткові знака цього числа після коми, ... |
|
| 398. |
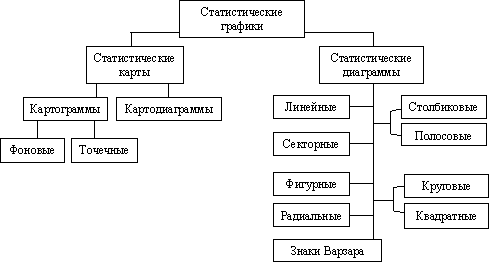
Статистическое наблюдение, первоначальная обработка и представление ее данных ... документ, который включает в себя адресную характеристику объекта наблюдения и статистические данные про него. Это могут быть переписные и отчетные листы, анкеты и т.п. Организационные вопросы статистического наблюдения Второй составляющей плана наблюдения являются организационные вопросы, ... |
|
| 399. |
Чисельні методи розв’язування крайових задач для звичайних диференціальних рівнянь ... ію і підставляючи вирази для похідних у рівняння (11.59), отримаємо крайову задачу з однорідними граничними умовами: , , . (11.71) Постановка задачі Щоб знайти єдиний розв'язок звичайного диференціального рівняння, необхідно задати деякі допоміжні умови, ... |
|
| 400. |
Статистическое моделирование ... совокупностью или просто выборкой объёма n будем называть совокупность n объектов, отобранных из интересующей нас генеральной совокупности. 2. Статистическая оценка законов распределения Если выборка объёма n из генеральной совокупности представительна, то элементы с одинаковыми ... |